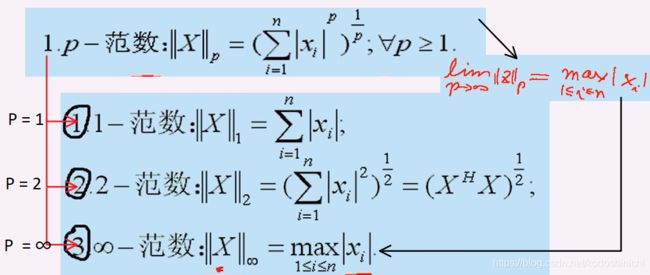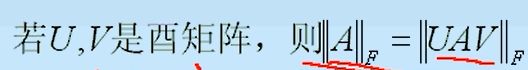【矩阵论】范数和矩阵函数（1）
范数及矩阵函数之范数的概念
首先将本章的内容做以下大致的梳理：
我们通过范数的概念来解决矩阵函数的问题，利用矩阵的函数可以解决很多实际问题。
一. 概念与定义
1. 范数与赋范线性空间
（1）范数——向量空间上的满足某些性质的实值函数
性质1称为范数的正定性（恒正性）
性质2称为范数的齐次性，其中因为k∈F，F可能是复数域，所以k值要取模值
性质3称为范数的三角不等式
（2）赋范线性空间
把定义了范数的线性空间称为是赋范线性空间
2. 常见的范数与赋范线性空间举例
（1）内积空间中的长度即是范数的一种
【回顾】内积空间就是定义了内积的线性空间：若F∈R，则为欧几里得空间；若F∈C，则为酉空间。
因为内积空间的长度是最常见也是很重要的一种范数，所以这一章在表示“范数”时，我们都使用记号||·||
注意：在谈论范数时，||·||并不是唯一指代向量长度。
（2）Cn中范数举例（p范数与范数的变换）
假设有任意向量X = (x1,x2,…,xn)T∈Cn
①P范数族
有关p范数是否满足范数定义的三性质，以下通过1-范数来举例说明：
【注】1-范数的“正定性”、“齐次性”和“三角不等式”性质的满足本质上是模运算的相应性质的满足。
上图中用黑框标注的地方就是证明的关键位。
②范数的变换
对于Cn空间上已知的范数定义，通过一个可逆矩阵A，即可相应得到另一种范数定义。
简要证明如下：
Tip：对于一个可逆矩阵A和一个非零向量x，Ax≠θ一定成立。可以用反证法论证。
（3）任意线性空间中的范数定义
换言之，就是对于任意给定的一个线性空间V(F∈C)；
找到该空间V上的一组基，V上的任意向量α在该组基上的坐标相应为X；
则V上的任意向量α的范数||α||V就可以转换成其坐标X向量(X∈Cn)在Cn空间中的范数||X||C^n^。
p.s. 而前面我们讨论了很多Cn空间行得通的范数定义，根据需要选用即可。
二. 范数与极限
此部分讲述定义“范数”概念的必要性。
定义范数是为了定义向量序列与向量的极限。
1. 矩阵序列与收敛
p.s. 矩阵序列的收敛是与选用的范数定义相关的。
2. 范数的可比较性
一言以蔽之，如果两个范数是可比较的，那么在这两个范数下所描述的矩阵序列的收敛性是等价的。
看回矩阵序列收敛的定义处，如果选用两个不同的范数，那么是否会存在相同的矩阵序列收敛于不同的值的情况？
——基于此，我们提出了范数的可比较性。
（1）定义
（2）证明与理解
以下进行证明“两个范数是可比较的 ↔ 矩阵序列在两个范数下的极限值是相同的”
Tip：既然“可比较”的定义中给出了不等式关系，证明时主要利用极限的夹逼准则。
若||ηi-η0||→0，则||ηi-η0||'→0
根据可比较的定义：
||ηi-η0||'≤(1/k1)||ηi-η0||→0；
||ηi-η0||'≥(1/k2)||ηi-η0||→0；
根据夹逼准则，有||ηi-η0||'→0。
若||ηi-η0||'→0，则||ηi-η0||→0
思路同上：
||ηi-η0||≤k2||ηi-η0||'→0；
||ηi-η0||≥k1||ηi-η0||'→0；
根据夹逼准则，有||ηi-η0||→0
（3）定理
有限维线性空间V上任意两个范数均是可比较的。
三. 矩阵范数
之前我们讨论的都是一般的线性空间的范数定义，以下我们讨论一个较为特殊的线性空间——矩阵空间上的范数定义。
1. 常见的矩阵范数的定义
（1）矩阵p-范数
如果把矩阵进行行分块或者列分块，每一个分块元素都可以套用之前Cn空间中定义的范数，从而就可以引出矩阵范数的相关定义。
- Frobenuis范数（||A||m2 = ||A||F）
这其中对矩阵2-范数要格外引起注意：
矩阵2-范数（Frobenius范数）对于酉变换保持不变性。
【证明】利用矩阵2-范数的定义可以对以上结论很好地进行证明
||A||F = (trAHA)1/2；
||UAV||F = (tr(UAV)H(UAV))1/2 = (tr(VHAHUHUAV))1/2
因为U是酉矩阵，所以满足UHU = I
||UAV||F = (trVHAHAV)1/2
因为V也是酉矩阵，所以满足VH = V-1
则||UAV||F = (trV-1AHAV)1/2，因为V-1AHAV与AHA一定是相似的，其二者具有相同的特征值
p.s. 矩阵的迹(tr)等于矩阵主对角线元素之和，也等于矩阵的全部特征值之和。
故证毕。
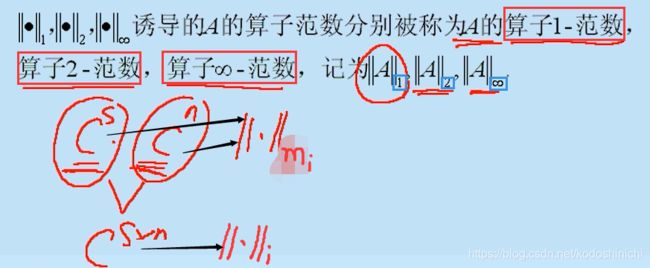
（2）算子范数
如果以线性变换的角度来看待一个矩阵，那么Amxn∈Cmxn这个矩阵可以看做把一个属于Cm空间中的向量X，映射成属于Cn空间中的向量AX。
基于这个线性映射的计算过程，我们同样也想要定义相对应的范数。
虽然此处不会深究讨论，但读者需要培养一个思维，当我们定义了上述的范数形式后，想要认可其确实可以作为一个范数，还需要思考以下问题：
- ||A||该范数是否有意义？
- ||A||该范数是否满足范数公理？
- 算子1范数，算子2范数和算子3范数
当原空间和变换空间分别取||·||mi(矩阵某范数），那么由此诱导出来的算子范数就是||·||i(相应的算子某范数)。
p.s. 这里一定要注意下标的表示方式，不要弄混了。
2. 矩阵范数的相容性
对于矩阵来说，其不仅有数乘、加法运算，还具有乘法运算。
数乘和加法运算针对于范数来说，根据范数定义中的齐性和三角不等式得到了规范；
但是乘法运算相应于范数还未有规范，至此我们提出“相容性”的概念。
（1）相容性的定义
（2）定理1——矩阵1范数，2范数相容，无穷大范数不相容
证明矩阵无穷大范数不相容，只需要给出反例即可
如上图考虑一个2阶全1方阵，其自身的无穷大范数为1；其2阶幂乘的结果是2阶的全2方阵，相应的无穷大范数为2；
显然不等式2≤1x1是不满足的。
故，不相容。
关于矩阵1范数与2范数的相容性，视频中未给出证明，读者可以自行尝试。
证明的思路可以借鉴下方链接中的证明题，利用范数的定义、性质进行不等式的放缩即可。
https://www.bilibili.com/read/cv4152269
（3）定理2——算子范数一定是相容的
也就意味着如果对于三个线性空间Cs,Cm和Cn，分别定义了其空间中的三个范数||·||Vs，||·||Vm和||·||Vn；
那么这三个范数又分别可以诱导出三个算子范数为||·||sxm，||·||sxn和||·||mxn。
“算子范数一定是相容的”，也就是说||·||sxm，||·||sxn和||·||mxn这三个范数是一定满足相容性的定义的。
（4）定理3——算子范数的求解
- 算子1范数就是最大的模长列和
- 算子2范数就是矩阵AHA的谱半径
- 算子无穷大范数就是最大的模长行和
以上三种算子范数中，谱范数是最重要的。
到此，有两个我们需要重点关注的矩阵范数，其一是矩阵2范数（Frobenuis范数），其二就是算子2范数（谱范数）。
【例】矩阵范数的求解 - 1
按照范数的定义相应代入计算即可。
拓展询问一下，若要求A(是一个酉矩阵)的矩阵2范数，那么根据定义——
||A||m2 = (tr(AHA))1/2 = (tr(I))1/2 = (n)1/2
- n阶酉矩阵的矩阵2范数为n1/2
- n阶酉矩阵的算子2范数为1
【例】矩阵范数的求解 - 2
[0]：解读题意，0号框所示就是我们的证明目标；
[1]：A是一个正规阵，那么A一定可以通过酉变换成为一个对角阵，将A用对角阵和酉矩阵相应表示出来；
[2]：按照算子2范数的定义，需要计算AHA及其谱半径，可知道其相似于ΛHΛ；
[3]：根据对角阵的运算，得到等式，两边同时开方即满足题意要求。
- 正规阵的算子2范数就是该矩阵的谱半径
【例】矩阵范数的求解 - 3
证明思路比较清晰，这里不再赘述，将例题中的结论提炼出来。
对于一个分块对角矩阵 - 其矩阵2范数就是各分块矩阵2范数的平方和再开方
- 其算子2范数就是各分块矩阵算子2范数中取最大值
记忆技巧：
矩阵2范数↔迹；算子2范数↔谱半径↔取最值
在分块对角中迹是相加的关系；
在分块对角中谱半径是再取最值的关系。