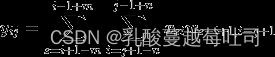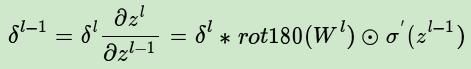NNDL 作业7：第五章课后题
目录
习题5-2 证明宽卷积具有交换性,即公式(5.13)
习题5-3 分析卷积神经网络中用1×1的卷积核的作用
习题5-4 对于一个输入为100×100×256的特征映射组，使用3×3的卷积核，输出为100×100×256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1×1的卷积核，先得到100×100×64的特征映射，再进行3×3的卷积，得到100×100×256的特征映射组，求其时间和空间复杂度
习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系
推导CNN反向传播算法（选做）
设计简易CNN模型，分别用Numpy、Pytorch实现卷积层和池化层的反向传播算子，并代入数值测试.(选做)
习题5-2 证明宽卷积具有交换性,即公式(5.13)
证明：
现有
根据宽卷积定义
为了让x的下标形式和w的进行对换，进行变量替换
令
故
则
已知
![i \in [1,M]J,J \in [1,N]](http://img.e-com-net.com/image/info8/e36826124105446eb032ab6dae12e9cd.jpg){kind=small}
因此对于
由于宽卷积的条件，s和t的变动范围是可行的。
习题5-3 分析卷积神经网络中用1×1的卷积核的作用
1、降维/升维
1x1卷积核可以通过控制卷积核数量实现降维或升维。
从卷积层流程图中可以清楚的看到 卷积后的特征图通道数与卷积核的个数是相同的。所以，如果想要升维或降维，只需要通过修改卷积核的个数即可。
举例：如果input的通道个数是3，卷积核个数为4，那么特征图的通道数就为4，达到了升维效果。 如果input的通道个数是3，卷积核个数为1，那么特征图的通道数就为1，达到了降维效果。
2、增加网络深度（增加非线性）
每使用 1x1卷积核，及增加一层卷积层，所以网络深度得以增加。 而使用 1x1卷积核后，可以保持特征图大小与输入尺寸相同，卷积层卷积过程会包含一个激活函数，从而增加了非线性。
在输入尺寸不发生改变的情况下而增加了非线性，所以会增加整个网络的表达能力。
3、 跨通道信息交互（通道的变换）
使用1x1卷积核，实现降维和升维的操作其实就是 channel 间信息的线性组合变化。
比如：在尺寸 3x3，64通道个数的卷积核后面添加一个尺寸1x1，28通道个数的卷积核，就变成了尺寸3x3，28尺寸的卷积核。 原来的64个通道就可以理解为跨通道线性组合变成了28通道，这就是通道间的信息交互。
注意：只是在通道维度上做线性组合，W和H上是共享权值的滑动窗口。
写的很好的文章：
深度学习 1x1卷积核的作用_高祥xiang的博客-CSDN博客_1*1卷积核的作用
卷积神经网络中1*1卷积的作用_m0_61899108的博客-CSDN博客
卷积神经网络CNN中1×1卷积作用理解_青衫憶笙的博客-CSDN博客_在cnn中使用1*1卷积时
习题5-4 对于一个输入为100×100×256的特征映射组，使用3×3的卷积核，输出为100×100×256的特征映射组的卷积层，求其时间和空间复杂度。如果引入一个1×1的卷积核，先得到100×100×64的特征映射，再进行3×3的卷积，得到100×100×256的特征映射组，求其时间和空间复杂度
时间复杂度一：256×100×100×256×3×3 = 5,898,240,000
空间复杂度一：256×100×100 = 2,560,000
时间复杂度二：64×100×100×256 + 256×100×100×64×3×3 = 1,638,400,000
空间复杂度二：64×100×100 + 256×100×100 = 3,200,000
习题5-7 忽略激活函数，分析卷积网络中卷积层的前向计算和反向传播是一种转置关系
以一个3×3的卷积核为例，输入为X输出为Y
将4×4的输入特征展开为16×1的矩阵，y展开为4×1的矩阵，将卷积计算转化为矩阵相乘
由
而
即
所以
再看一下上面的Y=CX可以发现忽略激活函数时卷积网络中卷积层的前向计算和反向传播是一种转置关系。
推导CNN反向传播算法（选做）
1、已知池化层的误差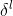
，反向推导上一隐藏层的误差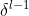
在前向传播算法时，池化层一般我们会用MAX或者Average对输入进行池化，池化的区域大小已知。现在我们反过来，要从缩小后的误差，还原前一次较大区域对应的误差。
在反向传播时，我们首先会把的所有子矩阵矩阵大小还原成池化之前的大小，然后如果是MAX，则把的所有子矩阵的各个池化局域的值放在之前做前向传播算法得到最大值的位置。如果是Average，则把的所有子矩阵的各个池化局域的值取平均后放在还原后的子矩阵位置。这个过程一般叫做upsample。
用一个例子可以很方便的表示：假设我们的池化区域大小是2x2。的第k个子矩阵为:
如果池化区域表示为a*a大小，那么我们把上述矩阵上下左右各扩展a-1行和列进行还原：
如果是MAX，假设我们之前在前向传播时记录的最大值位置分别是左上，右下，右上，左下，则转换后的矩阵为：
如果是Average，则进行平均，转换后的矩阵为：
上边这个矩阵就是误差矩阵经过upsample之后的矩阵，那么，由后一层误差推导出前一层误差的公式为：
2、已知卷积层的误差，反向推导上一隐藏层的误差
公式如下：
这里的式子其实和DNN的类似，普通网络的反向推导误差的公式：
区别在于对于含有卷积的式子求导时，卷积核被旋转了180度。即式子中的rot180()，翻转180度的意思是上下翻转一次，接着左右翻转一次。在DNN中这里只是矩阵的转置。
3、已知卷积层的误差，推导该层的W,b的梯度
经过以上各步骤，我们已经算出每一层的误差了，那么：
- 对于全连接层，可以按照普通网络的反向传播算法求该层W,b的梯度。
- 对于池化层，它并没有W,b,也不用求W,b的梯度。
- 只有卷积层的W,b需要求出，先看w：
再对比一下普通网络的求w梯度的公式，发现区别在于，对前一层的输出做翻转180度的操作：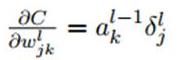
而对于b,则稍微有些特殊，因为在CNN中，误差δ是三维张量，而b只是一个向量，不能像普通网络中那样直接和误差δ相等。通常的做法是将误差δ的各个子矩阵的项分别求和，得到一个误差向量，即为b的梯度：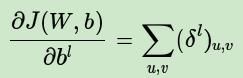
设计简易CNN模型，分别用Numpy、Pytorch实现卷积层和池化层的反向传播算子，并代入数值测试.(选做)
卷积层的反向传播：
import numpy as np
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride, padding):
super(Conv2D, self).__init__()
self.in_channels = in_channels
self.out_channels = out_channels
self.ksize = kernel_size
self.stride = stride
self.padding = padding
self.weights = np.random.standard_normal((out_channels, in_channels, kernel_size, kernel_size))
self.bias = np.zeros(out_channels)
self.grad_w = np.zeros(self.weights.shape)
self.grad_b = np.zeros(self.bias.shape)
def forward(self, x):
self.x = x
weights = self.weights.reshape(self.out_channels, -1) # o,ckk
x = np.pad(x, ((0, 0), (0, 0), (self.padding, self.padding), (self.padding, self.padding)), 'constant',
constant_values=0)
b, c, h, w = x.shape
self.out = np.zeros(
(b, self.out_channels, (h - self.ksize) // self.stride + 1, (w - self.ksize) // self.stride + 1))
self.col_img = self.im2col(x, self.ksize, self.stride) # bhw * ckk
out = np.dot(weights, self.col_img.T).reshape(self.out_channels, b, -1).transpose(1, 0, 2)
self.out = np.reshape(out, self.out.shape)
return self.out
def backward(self, grad_out):
b, c, h, w = self.out.shape #
grad_out_ = grad_out.transpose(1, 0, 2, 3) # b,oc,h,w * (bhw , ckk)
grad_out_flat = np.reshape(grad_out_, [self.out_channels, -1])
self.grad_w = np.dot(grad_out_flat, self.col_img).reshape(self.grad_w.shape)
self.grad_b = np.sum(grad_out_flat, axis=1)
tmp = self.ksize - self.padding - 1
grad_out_pad = np.pad(grad_out, ((0, 0), (0, 0), (tmp, tmp), (tmp, tmp)), 'constant', constant_values=0)
flip_weights = np.flip(self.weights, (2, 3))
# flip_weights = np.flipud(np.fliplr(self.weights)) # rot(180)
flip_weights = flip_weights.swapaxes(0, 1) # in oc
col_flip_weights = flip_weights.reshape([self.in_channels, -1])
weights = self.weights.transpose(1, 0, 2, 3).reshape(self.in_channels, -1)
col_grad = self.im2col(grad_out_pad, self.ksize, 1) # bhw,ckk
# (in,ckk) * (bhw,ckk).T
next_eta = np.dot(weights, col_grad.T).reshape(self.in_channels, b, -1).transpose(1, 0, 2)
next_eta = np.reshape(next_eta, self.x.shape)
return next_eta
def zero_grad(self):
self.grad_w = np.zeros_like(self.grad_w)
self.grad_b = np.zeros_like(self.grad_b)
def update(self, lr=1e-3):
self.weights -= lr * self.grad_w
self.bias -= lr * self.grad_b
def im2col(self, x, k_size, stride):
b, c, h, w = x.shape
image_col = []
for n in range(b):
for i in range(0, h - k_size + 1, stride):
for j in range(0, w - k_size + 1, stride):
col = x[n, :, i:i + k_size, j:j + k_size].reshape(-1)
image_col.append(col)
return np.array(image_col)
class Layers():
def __init__(self, name):
self.name = name
# 前向
def forward(self, x):
pass
# 梯度置零
def zero_grad(self):
pass
# 后向
def backward(self, grad_out):
pass
# 参数更新
def update(self, lr=1e-3):
pass
class Module():
def __init__(self):
self.layers = [] # 所有的Layer
def forward(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
def backward(self, grad):
for layer in reversed(self.layers):
layer.zero_grad()
grad = layer.backward(grad)
def step(self, lr=1e-3):
for layer in reversed(self.layers):
layer.update(lr)
# test_conv
if __name__ == '__main__':
x = np.array([[[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]]])
conv = Conv2D(2, 3, 2, 1, 0)
y = conv.forward(x)
print(y.shape)
loss = y - (y + 1)
grad = conv.backward(loss)
print(grad.shape)
池化层的反向传播：
import numpy as np
import torch.nn as nn
class MaxPooling(nn.Module):
def __init__(self, ksize=2, stride=2):
super(MaxPooling,self).__init__()
self.ksize = ksize
self.stride = stride
def forward(self, x):
n,c,h,w = x.shape
out = np.zeros([n, c, h//self.stride,w//self.stride])
self.index = np.zeros_like(x)
for b in range(n):
for d in range(c):
for i in range(h//self.stride):
for j in range(w//self.stride):
_x = i*self.stride
_y = j*self.stride
out[b, d ,i , j] = np.max(
x[b, d ,_x:_x+self.ksize, _y:_y+self.ksize])
index = np.argmax(x[b, d ,_x:_x+self.ksize, _y:_y+self.ksize])
self.index[b,d,_x+index//self.ksize, _y+index%self.ksize] = 1
return out
def backward(self, grad_out):
return np.repeat(np.repeat(grad_out, self.stride, axis=2), self.stride, axis=3) * self.index
总结：
这次作业，一直在和数学和公式打交道，对公式推导留下了深刻的印象，推导了宽卷积的交换性和CNN的反向传播算法，通过推导理解反向传播的公式和含义，加深了理解，同时对于1*1的卷积核的作用有了更深的理解。
参考：
深度学习 1x1卷积核的作用_高祥xiang的博客-CSDN博客_1*1卷积核的作用
卷积神经网络(CNN)反向传播算法 - 刘建平Pinard - 博客园
CNN的反向传播推导_BruceCheen的博客-CSDN博客_cnn反向传播算法 推导