线性回归——最小二乘法(公式推导和非调包实现)
接上一篇文章【线性回归——二维线性回归方程(证明和代码实现)】
前言:
博主前面一篇文章讲述了二维线性回归问题的求解原理和推导过程,以及使用python自己实现算法,但是那种方法只能适用于普通的二维平面问题,今天博主来讲一下线性回归问题中更为通用的方法,也是我们实际开发中会经常用到的一个数学模型,常用的解法就是最小二次乘法和梯度下降法.博主今天对最小二乘法进行推导并使用Python代码自定义实现,废话不多说,开始吧:
一、公式推导
- 假如现在有一堆这样的数据 ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) (x_1,y_1),(x_2,y_2),\dots,(x_n,y_n) (x1,y1),(x2,y2),…,(xn,yn),然后我们已经通过某种方式得到了数据所对应的模型 y ^ = θ 0 + θ 1 x \hat{y}=\theta_0+\theta_1x y^=θ0+θ1x,但是因为 y ^ \hat{y} y^ 毕竟是通过训练模型所得到的预测值,所以 y ^ \hat{y} y^ 与 y y y 之间必定存在误差如图所示:
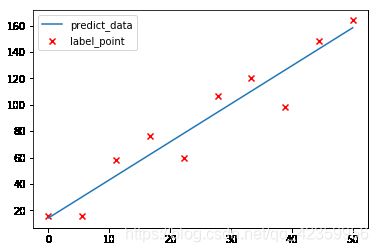
也就是说存在一个这样的等式 ω = y ^ − y \omega=\hat{y}-y ω=y^−y 其中 ω \omega ω 的值代表误差值.现在不妨我们再来将训练数据换一下变成 ( x 11 , x 12 , … , x 1 m , y 1 ) , ( x 21 , x 22 , , … , x 2 m , y 1 ) , … , ( x n 1 , x n 2 , … , x n m , y n ) (x_{11},x_{12},\dots,x_{1m},y_1),(x_{21},x_{22},,\dots,x_{2m},y_1),\dots,(x_{n1},x_{n2},\dots,x_{nm},y_n) (x11,x12,…,x1m,y1),(x21,x22,,…,x2m,y1),…,(xn1,xn2,…,xnm,yn)这里有n项数据,其中每项数据的前 m 个数据代表特征值,最后的一个数据代表标签值(也就是真实的 y 值),对这个数据我们通过线性模型也可以将数据对应的模型写出来: y ^ = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ m x m \hat{y}=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_mx_m y^=θ0+θ1x1+θ2x2+⋯+θmxm不妨简化一下换成矩阵的形式表示:
y ^ = ∑ i = 0 n θ i x i = θ T x \displaystyle \hat{y}=\sum_{i=0}^n{\theta_ix_i}=\theta^Tx y^=i=0∑nθixi=θTx
其中 θ = [ θ 0 θ 1 ⋮ θ m ] , x i = [ x i 0 x i 1 ⋮ x i m ] , x i 0 = 1 \theta=\begin{bmatrix}\theta_0 \\ \theta_1 \\ \vdots \\ \theta_m \end{bmatrix},x_i=\begin{bmatrix}x_{i0}\\x_{i1}\\ \vdots\\x_{im}\end{bmatrix},x_{i0}=1 θ=⎣⎢⎢⎢⎡θ0θ1⋮θm⎦⎥⎥⎥⎤,xi=⎣⎢⎢⎢⎡xi0xi1⋮xim⎦⎥⎥⎥⎤,xi0=1,我们再把 y ^ \hat{y} y^ 换一个符号表示:
y θ ( x i ) = ∑ i = 0 m θ i x i = θ T x i \displaystyle y_{\theta}(x_i)=\sum_{i=0}^m{\theta_ix_i}=\theta^Tx_i yθ(xi)=i=0∑mθixi=θTxi
上面这个函数方程即表示我们的拟合曲线,再结合我们前面分析的误差结论可知(因为误差值可正可负,这里加减就无所谓了):
y i = θ T x i + ω i y_i=\theta^Tx_i+\omega_i yi=θTxi+ωi
等式中的 右端项 y i y_i yi 代表真实的标签值,等式的左端项 θ T x i + ω i \theta^Tx_i+\omega_i θTxi+ωi 就代表预测值加上误差值
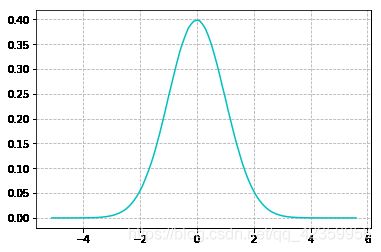
上图这个图应该很眼熟吧,没错就是表示正态分布(也称高斯分布)的统计图,其实现实生活中,误差的波动性也大多遵循这个规律.是什么意思呢?我们可以把图中的横坐标想作误差值,而纵坐标想成概率值,那么从图中我们可以发现一个很有意思的规律,误差值的绝对值越大那么它出现的概率反而会越小越趋近于0,误差值在0附近时可以看它们出现的概率是最大的,也就是说那种极大或者极小的误差值是占少数的.我们现在要引出一个函数也就是高斯分布的概率密度函数:
f ( x − μ ) = 1 2 π σ e ( − ( x − μ ) 2 2 σ 2 ) \displaystyle f(x-\mu)= \frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle (-\frac{(x-\mu)^2}{2\sigma^2})} f(x−μ)=2πσ1e(−2σ2(x−μ)2)
不懂概率密度函数的小伙伴也别急,你就把这个函数的自变量想成事件,然后函数的值想作此事件发生的概率即可;
- 既然误差遵循这个规律,那么我们就可以把前面我们得到的模型公式和概率密度函数联合起来就有:
{ y i = θ T x i + ω i f ( x − μ ) = 1 2 π σ e ( − ( x − μ ) 2 2 σ 2 ) \begin{cases} y_i=\theta^Tx_i+\omega_i \\ \displaystyle f(x-\mu)= \frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle (-\frac{(x-\mu)^2}{2\sigma^2})} \end{cases} ⎩⎪⎨⎪⎧yi=θTxi+ωif(x−μ)=2πσ1e(−2σ2(x−μ)2)
将 ω i \omega_i ωi 代入概率密度函数就有:
f ( ω i ) = 1 2 π σ e ( − ( y i − θ T x i ) 2 2 σ 2 ) \displaystyle f(\omega_i)=\frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle (-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})} f(ωi)=2πσ1e(−2σ2(yi−θTxi)2)
我们通常习惯用 p ( A ∣ B ) p(A|B) p(A∣B) 来表示B事件发生后A事件发生的概率,前面的公式也就可以变成:
p ( y i ∣ x i ; θ ) = 1 2 π σ e ( − ( y i − θ T x i ) 2 2 σ 2 ) \displaystyle p(y_i|x_i;\theta)=\frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle (-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})} p(yi∣xi;θ)=2πσ1e(−2σ2(yi−θTxi)2)
上式即表示我们通过训练模型得到准确值的概率,这个式子只是求单个数据得到真实值的概率,我们现在要来求全部数据都预测正确的概率,因为每个预测事件都是相互独立,的所以求全部正确概率只需要将所有单个的概率乘起来即可,那么就有:
L ( θ ) = ∏ i = 1 n p ( y i ∣ x i ; θ ) = ∏ i = 1 n 1 2 π σ e ( − ( y i − θ T x i ) 2 2 σ 2 ) \displaystyle L(\theta)=\prod_{i=1}^n{p(y_i|x_i;\theta)}=\prod_{i=1}^n{\displaystyle \frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle (-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})}} L(θ)=i=1∏np(yi∣xi;θ)=i=1∏n2πσ1e(−2σ2(yi−θTxi)2)
这个函数有个官方的名称叫做似然函数,它表示参数 θ \theta θ 所对应的模型预测值全部与真实值相匹配的概率,也可以把它看做预测模型与数据的真实模型的相似度,显然看着上面的式子都很头大,很难计算,不妨将它转化一下.两边同时取对数:
ln L ( θ ) = ln ∏ i = 1 n 1 2 π σ e ( − ( y i − θ T x i ) 2 2 σ 2 ) \displaystyle \ln{L(\theta)}=\ln{\prod_{i=1}^n{\displaystyle \frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle (-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})}}} lnL(θ)=lni=1∏n2πσ1e(−2σ2(yi−θTxi)2)
它表示对数似然函数,这里图方便后面化简就取以 e 为底的对数,去了对数之后不妨来看有什么好处,我们来化简一下:
因为对数内部的乘法可以展开为外部的加法即 l o g ( a b ) = log a + log b log{(ab)}=\log{a}+\log{b} log(ab)=loga+logb,所以:
ln L ( θ ) = ln 1 2 π σ e ( − ( y 1 − θ T x 1 ) 2 2 σ 2 ) + ⋯ + ln 1 2 π σ e ( − ( y n − θ T x n ) 2 2 σ 2 ) \displaystyle \ln{L(\theta)}=\ln{\displaystyle \frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle (-\frac{(y_1-\theta^Tx_1)^2}{2\sigma^2})}}+\cdots+\ln{\displaystyle \frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle (-\frac{(y_n-\theta^Tx_n)^2}{2\sigma^2})}} lnL(θ)=ln2πσ1e(−2σ2(y1−θTx1)2)+⋯+ln2πσ1e(−2σ2(yn−θTxn)2)
把它在弄好看一点:
ln L ( θ ) = ∑ i = 1 n ln 1 2 π σ e ( − ( y i − θ T x i ) 2 2 σ 2 ) \displaystyle \ln{L(\theta)}=\sum_{i=1}^n{\ln{\displaystyle \frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle (-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})}}} lnL(θ)=i=1∑nln2πσ1e(−2σ2(yi−θTxi)2)
再次利用对数的乘法变加法性质展开得:
ln L ( θ ) = n ln 1 2 π σ + ∑ i = 1 n ln e ( − ( y i − θ T x i ) 2 2 σ 2 ) \displaystyle \ln{L(\theta)}=n\ln{\frac{1}{\sqrt{2\pi}\sigma}}+\sum_{i=1}^n{\ln{e^{\displaystyle (-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})}}} lnL(θ)=nln2πσ1+i=1∑nlne(−2σ2(yi−θTxi)2)
我们都知对数有这样一个性质: log a a n = n \log_a{a^n}=n logaan=n 那么就有:
ln L ( θ ) = n ln 1 2 π σ + ∑ i = 1 n [ − ( y i − θ T x i ) 2 2 σ 2 ] \displaystyle \ln{L(\theta)}=n\ln{\frac{1}{\sqrt{2\pi}\sigma}}+\sum_{i=1}^n{\displaystyle \left[-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2}\right]} lnL(θ)=nln2πσ1+i=1∑n[−2σ2(yi−θTxi)2]
再把常数因子提到外边来就有:
ln L ( θ ) = n ln 1 2 π σ − 1 σ 2 1 2 ∑ i = 1 n ( y i − θ T x i ) 2 \displaystyle \ln{L(\theta)}=n\ln{\frac{1}{\sqrt{2\pi}\sigma}}-{\displaystyle \frac{1}{\sigma^2}\frac{1}{2}}\sum_{i=1}^n{(y_i-\theta^Tx_i)^2} lnL(θ)=nln2πσ1−σ2121i=1∑n(yi−θTxi)2
为了便于观察,我们把常数项用 t 来代替掉:
ln L ( θ ) = t 1 − t 2 1 2 ∑ i = 1 n ( y i − θ T x i ) 2 \displaystyle \ln{L(\theta)}=t_1-t_2\frac{1}{2}\sum_{i=1}^n{(y_i-\theta^Tx_i)^2} lnL(θ)=t1−t221i=1∑n(yi−θTxi)2
因为 ln L ( θ ) \ln{L(\theta)} lnL(θ) 表示的是训练模型与真实模型相似值,越大表明训练模型越趋近于真实模型,根据方程我们可以知道,等式右端第一项 t 1 ( n ln 1 2 π σ ) t_1(n\ln{\frac{1}{\sqrt{2\pi}\sigma}}) t1(nln2πσ1) 为一个非负常数,第二项中 t 2 ( 1 2 σ 2 ) t_2({\displaystyle \frac{1}{2\sigma^2}}) t2(2σ21)也为非负数,显然 t 2 1 2 ∑ i n ( y i − θ T x i ) 2 t_2{\displaystyle \frac{1}{2}\sum_i^n{(y_i-\theta^Tx_i)^2}} t221i∑n(yi−θTxi)2 也为非负数,所以一个正的常数项减去一个非负变量,似然函数的值越大越好,也就是需要让后面这个非负变量越小那么似然函数的值也就越大,于是就有:
J ( θ ) = 1 2 ∑ i = 1 n ( y i − θ T x i ) 2 J(\theta)=\displaystyle \frac{1}{2}\sum_{i=1}^n{(y_i-\theta^Tx_i)^2} J(θ)=21i=1∑n(yi−θTxi)2
现在我们目标就是求 max J ( θ ) \max{J(\theta)} maxJ(θ),我们根据表达式可以看出这是一个开口向上的二次函数,那么它必定存在一个极值点,而且这个极值点就是函数的最小值,所以我们只需对 J ( θ ) J(\theta) J(θ) 进行求导,然后使其等于 0 即可,我们先将上面的式子换一种方式表达:
我们令:
X = [ x 11 ⋯ x 1 m ⋮ ⋱ ⋮ x n 1 ⋯ x n m ] , Y = [ y 1 ⋮ y n ] X= \begin{bmatrix} x_{11}&\cdots&x_{1m} \\ \vdots&\ddots&\vdots\\ x_{n1}&\cdots&x_{nm} \end{bmatrix}, Y= \begin{bmatrix} y_1 \\ \vdots \\ y_n \end{bmatrix} X=⎣⎢⎡x11⋮xn1⋯⋱⋯x1m⋮xnm⎦⎥⎤,Y=⎣⎢⎡y1⋮yn⎦⎥⎤
那么就有:
J ( θ ) = 1 2 ( X θ − Y ) T ( X θ − Y ) J(\theta)=\displaystyle \frac{1}{2}(X\theta-Y)^T(X\theta-Y) J(θ)=21(Xθ−Y)T(Xθ−Y)
#######################补充说明(如果上面等式你已经理解是如何来到可以跳过下面的内容)#####################
可能有小伙伴不知道是如何变换过来的,其实你只要懂矩阵的乘法就可以了,很明显:
X θ = [ x 11 ⋯ x 1 m ⋮ ⋱ ⋮ x n 1 ⋯ x n m ] [ θ 1 ⋮ θ m ] = [ x 11 θ 1 + ⋯ + x 1 m θ m ⋮ ⋱ ⋮ x n 1 θ 1 + ⋯ + x n m θ m ] = [ θ T x 1 ⋮ θ T x n ] X\theta= \begin{bmatrix} x_{11}&\cdots&x_{1m} \\ \vdots&\ddots&\vdots\\ x_{n1}&\cdots&x_{nm} \end{bmatrix} \begin{bmatrix}\theta_{1} \\ \vdots \\ \theta_{m}\end{bmatrix}= \begin{bmatrix} x_{11}\theta_1+&\cdots&+x_{1m}\theta_m \\ \vdots&\ddots&\vdots \\ x_{n1}\theta_1+&\cdots&+x_{nm}\theta_m \end{bmatrix}= \begin{bmatrix} \theta^Tx_1\\ \vdots \\ \theta^Tx_n \end{bmatrix} Xθ=⎣⎢⎡x11⋮xn1⋯⋱⋯x1m⋮xnm⎦⎥⎤⎣⎢⎡θ1⋮θm⎦⎥⎤=⎣⎢⎡x11θ1+⋮xn1θ1+⋯⋱⋯+x1mθm⋮+xnmθm⎦⎥⎤=⎣⎢⎡θTx1⋮θTxn⎦⎥⎤即它的结果是一个 n 行 1 列的矩阵,那么:
( X θ − Y ) = [ θ T x 1 ⋮ θ T x n ] − [ y 1 ⋮ y n ] = [ θ T x 1 − y 1 ⋮ θ T x n − y n ] (X\theta-Y)= \begin{bmatrix} \theta^Tx_1\\ \vdots \\ \theta^Tx_n \end{bmatrix}-\begin{bmatrix} y_1 \\ \vdots \\ y_n \end{bmatrix}=\begin{bmatrix} \theta^Tx_1-y_1\\ \vdots \\ \theta^Tx_n-y_n \end{bmatrix} (Xθ−Y)=⎣⎢⎡θTx1⋮θTxn⎦⎥⎤−⎣⎢⎡y1⋮yn⎦⎥⎤=⎣⎢⎡θTx1−y1⋮θTxn−yn⎦⎥⎤
所以:
( X θ − Y ) T ( X θ − Y ) = [ θ T x 1 − y 1 , ⋯ θ T x n − y n ] [ θ T x 1 − y 1 ⋮ θ T x n − y n ] = ( θ T x 1 − y 1 ) 2 + ⋯ + ( θ T x n − y n ) 2 = ∑ i n ( y i − θ T x i ) 2 (X\theta-Y)^T(X\theta-Y)= \begin{bmatrix} \theta^Tx_1-y_1,\cdots \theta^Tx_n-y_n \end{bmatrix} \begin{bmatrix} \theta^Tx_1-y_1\\ \vdots \\ \theta^Tx_n-y_n \end{bmatrix}\\= (\theta^Tx_1-y_1)^2+\cdots+(\theta^Tx_n-y_n)^2\\= \displaystyle \sum_i^n{(y_i-\theta^Tx_i)^2} (Xθ−Y)T(Xθ−Y)=[θTx1−y1,⋯θTxn−yn]⎣⎢⎡θTx1−y1⋮θTxn−yn⎦⎥⎤=(θTx1−y1)2+⋯+(θTxn−yn)2=i∑n(yi−θTxi)2
############################################ 结束 ################################################# - 现在我们对 J ( θ ) J(\theta) J(θ) 进行求偏导那么就有:
δ ( J ( θ ) ) δ θ = 1 2 δ ( ( X θ − Y ) T ( X θ − Y ) ) δ θ \displaystyle \frac{\delta(J(\theta))}{\delta\theta}=\frac{1}{2}\frac{\delta((X\theta-Y)^T(X\theta-Y))}{\delta\theta} δθδ(J(θ))=21δθδ((Xθ−Y)T(Xθ−Y))
将转置放在里面来(注意在对含有乘法的项转置时要将矩阵变换顺序):
δ ( J ( θ ) ) δ θ = 1 2 δ ( ( θ T X T − Y T ) ( X θ − Y ) ) δ θ \displaystyle \frac{\delta(J(\theta))}{\delta\theta}=\frac{1}{2}\frac{\delta((\theta^TX^T-Y^T)(X\theta-Y))}{\delta\theta} δθδ(J(θ))=21δθδ((θTXT−YT)(Xθ−Y))
使用分配律将括号展开:
δ ( J ( θ ) ) δ θ = 1 2 δ ( θ T X T X θ − Y T X θ − θ T X T Y + Y T Y ) δ θ \displaystyle \frac{\delta(J(\theta))}{\delta\theta}=\frac{1}{2}\frac{\delta(\theta^TX^TX\theta-Y^TX\theta-\theta^TX^TY+Y^TY)}{\delta\theta} δθδ(J(θ))=21δθδ(θTXTXθ−YTXθ−θTXTY+YTY)
在最终求导前要先介绍三个矩阵求导的性质:
性质一:
如果有 f ( A ) = A T B A f(A)=A^TBA f(A)=ATBA 那么 δ ( f ( A ) ) δ A = B A + B T A \displaystyle \frac{\delta(f(A))}{\delta A}=BA+B^TA δAδ(f(A))=BA+BTA
性质二:
如果有 f ( A ) = B T A f(A)=B^TA f(A)=BTA 那么 δ ( f ( A ) ) δ A = B \displaystyle \frac{\delta(f(A))}{\delta A}=B δAδ(f(A))=B
性质三:
如果有 f ( A ) = A T B C f(A)=A^TBC f(A)=ATBC 那么 δ ( f ( A ) ) δ A = B C \displaystyle \frac{\delta(f(A))}{\delta A}=BC δAδ(f(A))=BC
有了上面三个性质,现在就可以计算上面式子的导数了(先做一下变换,方便使用上面的性质)
δ ( J ( θ ) ) δ θ = 1 2 δ ( θ T ( X T X ) θ − ( X T Y ) T θ − θ T X T Y + Y T Y ) δ θ \displaystyle \frac{\delta(J(\theta))}{\delta\theta}= \frac{1}{2}\frac{\delta(\theta^T(X^TX)\theta-(X^TY)^T\theta-\theta^TX^TY+Y^TY)}{\delta\theta} δθδ(J(θ))=21δθδ(θT(XTX)θ−(XTY)Tθ−θTXTY+YTY)
利用性质一,二,三可得:
δ ( J ( θ ) ) δ θ = 1 2 [ ( ( X T X ) θ + ( X T X ) T θ ) − X T Y − X T Y ] \displaystyle \frac{\delta(J(\theta))}{\delta\theta}= \frac{1}{2}\left[((X^TX)\theta+(X^TX)^T\theta)-X^TY-X^TY\right] δθδ(J(θ))=21[((XTX)θ+(XTX)Tθ)−XTY−XTY]
将转置放在扩号中去:
δ ( J ( θ ) ) δ θ = 1 2 [ ( X T X θ + X T X θ ) − X T Y − X T Y ] \displaystyle \frac{\delta(J(\theta))}{\delta\theta}= \frac{1}{2}\left[(X^TX\theta+X^TX\theta)-X^TY-X^TY\right] δθδ(J(θ))=21[(XTXθ+XTXθ)−XTY−XTY]
合并同类项:
δ ( J ( θ ) ) δ θ = 1 2 ( 2 X T X θ − 2 X T Y ) = X T X θ − X T Y \displaystyle \frac{\delta(J(\theta))}{\delta\theta}= \frac{1}{2}\left(2X^TX\theta-2X^TY\right)=X^TX\theta-X^TY δθδ(J(θ))=21(2XTXθ−2XTY)=XTXθ−XTY
因为我们要求极值点,所以令导数等于0即可:
δ ( J ( θ ) ) δ θ = X T X θ − X T Y = 0 \displaystyle \frac{\delta(J(\theta))}{\delta\theta}=X^TX\theta-X^TY=0 δθδ(J(θ))=XTXθ−XTY=0
移项得:
X T X θ = X T Y X^TX\theta=X^TY XTXθ=XTY
两边同时乘以一个 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1:
θ = ( X T X ) − 1 X T Y \theta=(X^TX)^{-1}X^TY θ=(XTX)−1XTY
这样我们便得到了 θ \theta θ的计算方法
二、代码实现
- 有了计算方式,那么使用代码来实现就简单了
- 先定义计算 θ \theta θ 的函数
import matplotlib.pyplot as plt
import numpy as np
def train_model(x_data,y_data):
# 逻辑很简单就是把求theta的公式实现了一遍
matrix_x = np.matrix(x_data)
matrix_y = np.matrix(y_data)
matrix_x_T = matrix_x.T
t1 = np.dot(matrix_x_T,matrix_x)
t1_I = t1.I
t2 = np.dot(t1_I,matrix_x_T)
theta = np.dot(t2,matrix_y)
return theta
- 定义使用模型进行预测的函数:
def predict(model,x_data):
# 这里因为我们传入的x_data是 n×m,model是 m×1,所以反过来乘代码逻辑就会简单许多
return np.dot(np.matrix(x_data),model)
- 加载数据
# 导入自带的波士顿房价数据
from sklearn.datasets import load_boston
boston_data = load_boston().data
train_x = boston_data[:,:-1]
# 这里需要注意的波士顿原本数据内只有12个特征值,前面也说过我们的模型有一个单出来的 theta0
# 那么我们只需要在数据中认为的假如一列特征列,全部置一即可
# 也就是 t_0x_0+t_1x_1+...+t_12x_12
# 我们把方程中的t_0全部变为1即可
ones_x = np.ones(train_x.shape[0])
train_x = np.column_stack((ones_x,train_x))
train_y = boston_data[:,-1:]
- 训练模型
model = train_model(train_x,train_y)
model.shape
# (13,1)
- 预测数据
p_y = predict(model,train_x)
p_y = np.sort(np.array(p_y)[:,0])
- 在图上绘制数据
plt.scatter(np.arange(0,506),np.sort(boston_data[:,-1]),marker="x",c="r",label="label_data")
plt.plot(np.arange(0,506),p_y,label="predict_data")
plt.legend()
写在最后的话:
感觉这篇文章写了好久,写这篇文章发现了几个自身的问题,矩阵的求导方法还不是很熟悉,矩阵的有一些基本性质有遗忘现象.
感觉线性代数和高数还是要时不时的回去复习一下,不然会越学越吃力,怎么说了写博客还是收益挺多了,凡是不能图快,要是地基都没打牢,房子搭在高也是会倒的,万丈高楼平地起.嗯.
最后如果有小伙伴发现文章有什么错误的地方,欢迎指出来,将非常感谢!!!(__)
