数字图像处理练习题整理 (三)

• 注: 内容仅供参考, 不保证正确性, 如有误欢迎交流指正.
• 鸣谢: 感谢 小组的各位同学为内容整理提供的帮助

七. 边缘检测

1. Canny算子

请写出Canny算子检测边缘的详细步骤。
Canny边缘检测算法可以分为一下五个步骤：

1. 使用高斯滤波器，以平滑图像，滤除噪声。
2. 计算图像中每个像素点的梯度强度和方向。
3. 根据梯度方向，对梯度幅值应用非极大值抑制（non-maximum suppression）。
4. 应用双阈值（Double-Threshold）检测来确定真实的和潜在的边缘。
5. 通过抑制孤立的弱边缘最终完成边缘检测

1. 使用高斯滤波器，以平滑图像，滤除噪声。
高斯滤波使用的高斯核是具有x和y两个维度的高斯函数，且两个维度上标准差一般取相同，形式为：

$G(X,Y)=\sum _{x-m}^{x+m}\sum _{y-m}^{y+m}exp|-\frac{x^2+y^2}{2{\sigma }^2}|$ ，$m=\frac{n-1}{2}$，$n$表示高斯滤波器窗口大小
高斯滤波其实就是将所指像素用周围的像素的某种均值代替(即卷积核)，卷积核尺寸越大，去噪能力越强，因此噪声越少，但图片越模糊，canny检测算法抗噪声能力越强，但模糊的副作用也会导致定位精度不高。

2. 计算图像中每个像素点的梯度强度和方向。
图像中的边缘可以指向各个方向，因此Canny算法使用四个算子来检测图像中的水平、垂直和对角边缘。边缘检测的算子（如Roberts，Prewitt，Sobel等）返回水平$G_x$和垂直$G_y$方向的一阶导数值，由此便可以确定像素点的梯度$G$和方向$\theta$。下面以Sobel算子为例讲述如何计算梯度强度和方向。
Sobel算子是两个 3×3 的矩阵，分别为$S_x$和$S_y$和前者用于计算图像$X$方向像素梯度矩阵$G_x$，后者用于计算图像$Y$方向像素梯度矩阵 $G_y$。具体形式为：

$G_x=S_x\ast I=\left[\begin{array}{ccc}-1& 0& +1\\ -2& 0& +2\\ -1& 0& +1\end{array}\right]\ast I$， $G_y=S_y\ast I=\left[\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ +1& +2& +1\end{array}\right]\ast I$， $I$为灰度图像矩阵，由此可得梯度强度矩阵和方向
$G=\sqrt{G_x^2+G_y^2}$ $\theta =\arctan (\frac{G_y}{G_x})$
其中$G$为梯度强度， $\theta$表示梯度方向，$\arctan$为反正切函数。

3. 根据梯度方向，对梯度幅值应用非极大值抑制（non-maximum suppression）。
非极大值抑制的做法为：其基本方法是将当前像素梯度强度与沿正负梯度方向上的相邻像素的梯度强度进行比较，若其最大（即为极值），则保留该像素为边缘点，若不是最大，则对其进行抑制，不将其作为边缘点。如图所示，可将像素的邻接情况划分为4个区域，其中每个区域包含上下两部分。沿梯度方向检测模值的极大值点，即边缘点，遍历8个方向图像像素，把每个像素偏导值与相邻像素的模值比较，取其MAX值为边缘点，置像素灰度值为0.

算法过程如下：
$\tan (\theta )=\frac{G_y}{G_x}$
$G_{p_1}=(1-\tan (\theta ))\times G_E+\tan (\theta )\times G_{NE}$
$G_{p_2}=(1-\tan (\theta ))\times G_W+\tan (\theta )\times G_{SW}$
如果$G_p\ge G_{p_1}$ 且 $G_p\ge G_{p_2}$，$G_p$ 应该成为边缘点否则应该对$G_P$进行抑制。剩余的三个区域计算方法类似。

4. 应用双阈值（Double-Threshold）检测来确定真实的和潜在的边缘。
施加非极大值抑制后，剩余像素可以更准确地表示图像中的实际边缘。但仍然存在由于噪声和颜色变化引起的一些边缘像素。为了解决这些杂散响应，必须用弱梯度值过滤边缘像素，并保留具有高梯度值的边缘像素，可以通过选择高低阈值来实现。如果边缘像素的梯度值高于高阈值，则将其标记为强边缘像素；如果边缘像素的梯度值小于高阈值并且大于低阈值，则将其标记为弱边缘像素；如果边缘像素的梯度值小于低阈值，则会被抑制。
算法描述：
if $G_p\ge HighThreshold$
​ $G_p$ is an strong edge
else if $G_p\ge LowThreshold$
​ $G_p$ is an weak edge
else
​ $G_p$ should be suppressed

• 选取系数TH和TL，比率为2:1或3:1。（一般取TH=0.3或0.2,TL=0.1）；将小于低阈值的点抛弃，赋0；
• 将大于高阈值的点立即标记（这些点为确定边缘点），赋1或255
• 将小于高阈值，大于低阈值的点即为弱边缘点。
  对于弱边缘点，采用八连通区域确定。

5. 通过抑制孤立的弱边缘最终完成边缘检测
到目前为止，被划分为强边缘的像素点已经被确定为边缘，因为它们是从图像中的真实边缘中提取出来的。然而，对于弱边缘像素，将会有一些争论，因为这些像素可以从真实边缘提取也可以是因噪声或颜色变化引起的。为了获得准确的结果，应该抑制由后者引起的弱边缘。通常，由真实边缘引起的弱边缘像素将连接到强边缘像素，而噪声响应未连接。为了跟踪边缘连接，通过查看弱边缘像素及其8个邻域像素，只要其中一个为强边缘像素，则该弱边缘点就可以保留为真实的边缘。
算法描述：
if $G_p==LowThreshold$ and $G_p$ connected to a strong edge pixel
​ $G_p$ is an strong edge
else
​ $G_p$ should be suppressd

2. LoG算子

请写出LoG（Laplacian Of Gaussian）算子的计算方法。
高斯拉普拉斯算子（$LoG$)：
对于图像 $I(x,y)$, 首先通过尺度为 $\sigma$ 的高斯平滑：
$$G_{\sigma }(x,y)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (-\frac{x^2+y^2}{2{\sigma }^2})$$
接着使用拉普拉斯算子检测边缘：
$${\nabla }^2|G_{\sigma }(x,y)\ast I(x,y)|=[{\nabla }^2{G}_{\sigma }(x,y)]\ast I(x,y)$$
该式证明如下：
$$\begin{array}{rl}\frac{d}{d{t}^2}[h(t)\ast f(t)]& =\frac{d}{dt}\int f(\tau )h(t-\tau )d\tau \\ & =\int f(\tau )\frac{d}{d{t}^2}h(t-\tau )d\tau \\ & =f(t)\ast \frac{d}{d{t}^2}h(t)\end{array}$$
所以高斯拉普拉斯算子等价于先对高斯函数求二阶导，再与原图进行卷积，将LoG算子展开即为：
$$LoG={\nabla }^2{G}_{\sigma }(x,y)=\frac{{\partial }^2{G}_{\sigma }(x,y)}{\partial x^2}+\frac{{\partial }^2{G}_{\sigma }(x,y)}{\partial y^2}=\frac{x^2+y^2-2{\sigma }^2}{2\pi {\sigma }^6}\exp (-\frac{x^2+y^2}{2{\sigma }^2})$$

写出DoG （Difference Of Gaussian）算子的计算方法。
高斯函数差分算子（$DoG$）:

$DoG$即对不同尺度下的高斯函数的差分。DoG算子的表达式如下：
$$DoG=G_{{\sigma }_1}-G_{{\sigma }_2}=\frac{1}{\sqrt{2\pi }}[\frac{1}{{\sigma }_1}{e}^{-(x^2+y^2)/(2{\sigma }_1^2)}-\frac{1}{{\sigma }_2}{e}^{-(x^2+y^2)/(2{\sigma }_2^2)}]$$

DoG与LoG之间有何关系？
DoG算子可以用来近似LoG算子。DoG算子和LoG算子具有类似的波形，仅仅是幅度不同，不影响极值点的检测，而DoG算子的计算复杂度显然低于LoG，因此一般使用DoG代替LoG算子。
DoG算子是高斯函数的差分，具体到图像中，就是将图像在不同参数下的高斯滤波结果相减，得到差分图。LoG先对高斯核函数求取二阶导数，再与原图像进行卷积操作。LoG算子和DoG算子既可以用于检测图像边缘，也可用于检测局部极值点或极值区域。

相似性证明如下
因为，
$$\frac{\partial G}{\partial \sigma }=\frac{x^2+y^2-2{\sigma }^2}{2\pi {\sigma }^5}{e}^{\frac{x^2+y^2}{2{\sigma }^2}}$$
由上述的定义得
$$\frac{\partial G}{\partial \sigma }=\sigma {\nabla }^{2}G$$
由导数的定义得：
$$\frac{\partial G}{\partial \sigma }=\underset{\Delta \sigma \to 0}{\lim }\frac{G(x,y,\sigma +\Delta \sigma )-G(x,y,\sigma )}{\Delta \sigma }\approx \frac{G(x,y,\sigma +k\sigma )-G(x,y,\sigma )}{k\sigma -\sigma }$$
则
$$\sigma {\nabla }^{2}G\approx \frac{G(x,y,\sigma +k\sigma )-G(x,y,\sigma )}{k\sigma -\sigma }$$
变形得
$$G(x,y,\sigma +k\sigma )-G(x,y,\sigma )\approx (k-1){\sigma }^2{\nabla }^{2}G$$

利用LoG算子对图像进行处理，可以得到何种信息？
LoG算子就是先对图像进行高斯模糊，然后再求二阶导数，二阶导数等于0处对应的像素就是图像的边缘，即得到图像的边缘信息。

3. 边界跟踪

设一幅二值图像中，只有一个白色区域，试给出求该区域外围轮廓线的方法（要求按顺时针的顺序给出各点的坐标，即行/列号）。

1. 令起点$b_0$为图像中左上角标记为1的点，用$c_0$表示$b_0$西侧的点，很显然，$c_0$总是背景点。从$c_0$开始按顺时针方向考察$b_0$的8个邻接点，令$b$表示所遇到的值为1的第一个邻接点，并直接令$c_1$是序列$b_1$之前的点，存储$b_0$和的$b_1$位置，以便在步骤5中使用。
2. 令$b$=$b_1$和$c$=$c_1$
3. 从 $c$ 开始按顺时针方向行进，令 $b$ 的8个邻接点为 $n_1$,$n_2$,…,$n_8$。找到标为 1 的第一个 $n_k$
4. 令 $b$=$b_k$ 和 $c$=$c_k$
5. 重复步骤 3 和 4，直到 $b$=$b_0$ 就找到了下一个边界点为 $b_1$.
6. 当算法停止时，所找到的 $b$ 点的序列就构成了排列后的边界点的集合。

• 拓展: 按逆时针方向进行边界跟踪：
  搜索顺序表

3	2	1
4	x	0
5	6	7

1. 对图像进行逐行查找（从上到下，从左到右），找到第一个值为1的点，用$P_0$表示。
   $P_0$：边界跟踪的起始点。
   定义变量 dir：搜索方向（1，…，7）dir=7；

2. 按逆时针方向顺序依次判断当前点（一开始为 $P_0$ 点）8个 3×3 邻居是否为 1，开始的邻居号为：

   1. （dir+7）mod 8 如果当前的dir为偶数；
   2. （dir+6）mod 8 如果当前的dir为奇数；
      按上述的逆时针方向找到的第一个不为 0 的点为找到的新的边界，记为 $P_n$，并更新 dir 值（以当前找到为1的点为最后更新的 dir 方向）。

3. 如果当前的边界点 $P_n$ 的坐标等于找到的第二个边界点 $P_1$ 的坐标，而且它前一个边界点 $P_{n-1}$ 的坐标又与起始点 $P_0$ 坐标相同，则算法结束。否则，重复步骤 2

4. 图像分割与求最小代价路径

设在一幅图像中分割出一个区域，如何将目标分割问题转换为一个求最小代价路径的问题？

1. 识别地标(Landmark)。对每个地标点$P_i$，图像中个$m$最可能的位置只根据它的密度形式来选择。为了选择这些位置，我们使用密度损失函数$h_i(p,I)$扫描整个图像或图像中一个最相关的部分。点$P_{i,1},P_{i,2},P_{i,m}$对应$m$个最小的灰度损失将成为每$i$个地标的候选。每个地标的$m$个最好的位置被选中后，算法将构造一个$n\times m$的灰度损失矩阵，$C$中的第$i$行包含了地标$i$的$m$个最可能位置的损失：
   
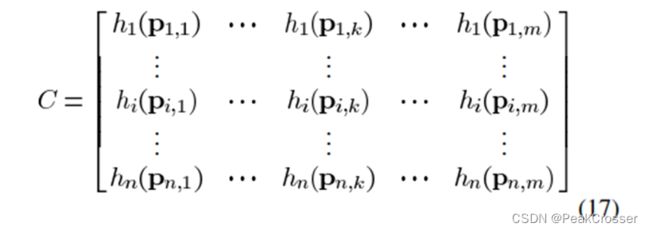
2. 最小代价路径。找到分割一个目标的轮廓被转化为找到C中的一条最优路径。图像分割问题因此转化成了找到一条路径$(k_1^{\ast },k_2^{\ast },\dots k_n^{\ast })$使得下面的某个损失函数最小化：
   $$(k_1^{\ast },k_2^{\ast },\dots k_n^{\ast })=\underset{k_1^{\ast },\dots k_n^{\ast }}{\mathrm{argmin}}\mathcal{J}(k_1^{\ast },\dots k_n^{\ast })$$
   损失（代价）有两种：
   1. 分配给每条路径结点i的地标候选的密度损失$h_i$
   2. 从结点i转移到结点i+1的形状损失$f_i$

从而，目标函数可以为：
$$\mathcal{J}(k_1^{\ast },\dots k_n^{\ast })=\sum _{i=1}^b{h}_i+\gamma \sum _{i=1}^n{f}_i$$
$$h_i=h_i(P_i,k_i)$$
$$f_i=f_i(P_{i+1,k_i+1}-P_{i,k_i})$$
或者
$$f_i=f_i(P_{i+1,k_i+1}-P_{i,k_i},P_{i,k_i}-P_{i-1,k_i-1})$$
基于图论的分割方法就是把要进行分割的图像看成是一个带权无向图。原图像中的各像素点就是带权无向图中的结点。边是在各结点之间形成的。边的权值$W(i,j)$可以反正出顶点i与顶点j之间的相似程度，其可以由空间关系(如顶点i到顶点j的距离)与灰度测试(如纹理、颜色、灰度值)形成。我们可以将原带权无向图按照每各个像素之间的相似程度切割成若干个子集区域。每个子集区域内的像素相似度比较高，不同的子集区域的像素相似性较低。切割的过程实际上就是去除相似度低的结点之间的边。

代价可以包括哪些因素？

• 梯度代价: 平面拟合、径向梯度、归一化
• 灰度代价: 边界灰度估计
• 结点间距离代价

八. 形态运算

1. 图像腐蚀

设有一幅二值图像，采用 3×3的结构元（每个元素均为1）对其进行腐蚀操作，试写出得到结果图像的方法。
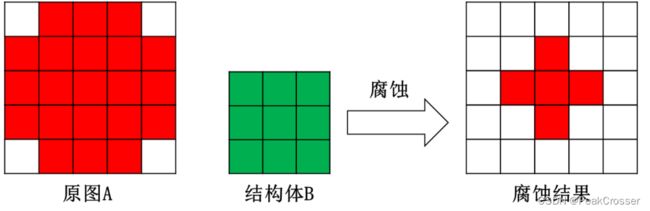
腐蚀处理的结果是使原来的二值图像减小一圈, 原图A被结构B腐蚀的定义如下，z代表B的中心位置:
$$A\odot B=\{z|(B{)}_z\subseteq A\}$$
可以理解为，移动结构B，如果结构B完全属于原图A的区域内，则保存该位置点，所有满足条件的点构成结构A被结构B腐蚀的结果。

用结构体B对原图A进行腐蚀的整个过程如下：

1. 将 3*3 的结构元B在A中移动，即让B的中心循环扫描图像A的每一个像素。
2. 用结构元素B的每个位置与其覆盖的二值图像对应的位置做“与”操作
3. 如果步骤 2 结果中所有像素结果都为 1，也即结构体B完全包含在A中，则此时目标图像对应B的中心位置像素为1; 否则为0。

示例结果如下, 有颜色代表像素为1，空白代表像素为0 ：

2. 孔洞填充

试写出孔洞填充的算法。对二值图像中所有被白色区域包围（封闭）的黑色像素即为孔洞。
孔洞填充的公式为：
$$X_k=(X_{k-1}\oplus B)\cap A^{c}k=1,2,3,...$$
设原包含孔洞的图像为A，原图补集为$A^c$，用于填充膨胀的结构体为B，则孔洞填充算法流程：

1. 将原图像 A 每个像素取反，获得补集原图像的补集记作$A^c$，用来限制膨胀结果在孔洞内，防止膨胀超出孔洞区域范围；
2. 在原图孔洞中选择一个初始点，使用结构体B膨胀该点；
3. 将膨胀后的结果与原图补集 $A^c$ 相交，得到该轮次的结果 $X_k$。
4. 在原图孔洞中移动到下一个点，重复步骤 2~4，直到第 K 步和第 K+1 步结果相同，填充完毕。

上述算法步骤中使用了膨胀操作，下面简述膨胀操作过程：
膨胀处理的结果是使原来的二值图像扩大一圈, 原图A被结构B膨胀的定义如下，z代表B的中心位置:

$$A\oplus B=\{z|(\hat{B}{)}_z\bigcap A\ne \varnothing \}$$
上式中$(\hat{B}{)}_z$是结构体关于中心圆点反转的结构，膨胀可以理解为，移动结构B的反转结构$(\hat{B}{)}_z$，如果与原图A存在重叠区域，也即交集不为空，则此时结构体中心位置对应在目标图结果中处像素为1，反之没有交集则为0。

3. 粘连区域断开

设有两个白色区域，被一条细小的白线所连接，试设计一种算法，消除两个区域之间的细线，使两个区域分开。
使用开运算即可，开运算等于对原图先腐蚀后膨胀，可以用来消除小物体、在纤细点处分离物体、消除物体周围的毛刺等。设原图为A，结构体为B开运算的公式为：
$$A\circ B=(A\odot B)\oplus B$$
分割两个细小白线连接的白色区域的步骤如下：

1. 设置开运算结构B为N*N, N的大小根据细线的宽度而更改，要比细线宽度大。
2. 先对原图A使用结构体B进行腐蚀运算。
3. 对步骤 2 的结果再次使用结构体B进行膨胀运算。

• 注意: 上述开运算步骤中使用了腐蚀和膨胀运算，这两种算法见前两题图像腐蚀和孔洞填充中介绍，这里不再赘述。

4. 计算凸壳

计算包围给定点集的最小凸多变形。
采用安德鲁算法计算最小凸包，流程简述如下：

1. 将给定的点集合按照x坐标升序排列。x相同的话，按照y坐标升序排列
2. 创建凸包的上部U点序列：默认将x最小的两个点加入上凸包U，再将排序后的点按照x坐标从小到大的顺序依次加入凸包U，并检查U是否仍然为凸包。如果新加入的点使得U不再是凸多边形，那么就逆序依次删除已经插入U的点，直到U为凸多边形。
3. 创建凸包的下部L点序列：默认将x最大的两个点加入下凸包L, 再将排序后的点按照x坐标从大到小的顺序加入凸包L，并检查L是否仍然为凸包。如果新加入的点使得L不再是凸多边形，那么就逆序删除已经插入L的点，直到L为凸多边形。
4. 连接凸包的上部和下部： 最终外接凸多边形点集为凸包上部的点序列+凸包下部逆置后的点序列(下部形成是按照x从大到小，要逆序形成从小到大的序列)，每两个点之间连线，最后一个点和第一个点连线即是最终外接凸多边形。

检查是否为凸包的方法如下：
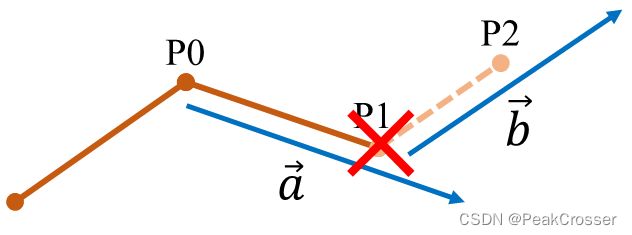
设将要加入点$P_2$，凸包集中上一轮加入的节点为$P_1$, 上上一轮加入的节点为$P_0$ , 则形成两个向量： $a=P_0\to P_1$和 $b=P_0\to P_2$。如果$a\times b<0$, 则说明第二个向量$b$位于第一个向量$a$的逆时针处, 此时新加入节点$P_2$会使结果不再是凸边形，需要逆序删除已经插入的点，直到加入$P_2$后，保持凸包。
上述判断方法示意图如下, 此时加入P2会使第二个向量$b$位于第一个向量$a$的逆时针处，凸包被破坏，需要逆序删除P1点。