统计学习方法 第三章习题

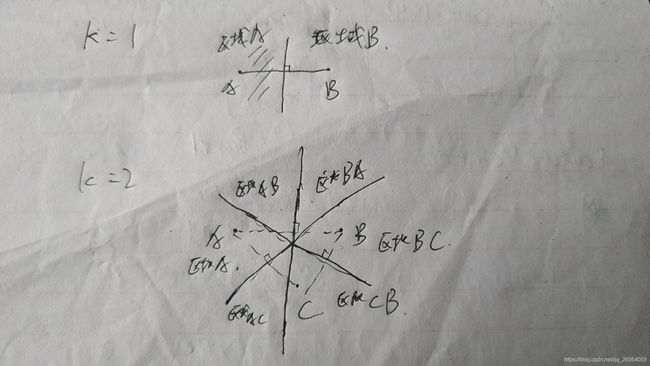
3.1参照图3.1，在二维空间中给出实例点，画出k为1和2时的k近邻法构成的空间划分，并对其进行比较，体会k值选择与模型复杂度及预测准确率的关系。

k=1比较好理解，就是各自为政，自己有自己的一块区域，书上的图3.1即为k=1时，两个或多个点互相连接找连接线中垂线，以中垂线划分区域；

而k=2也是找垂线但是垂线互相交叉，划分多个区域找区域相近的两个点一个单元，如下图中的区域AB为AB近邻但与A更近，这样可以推广为多个点

k=3可能在二维点上无法划分，可能需要在三维上去画图

 

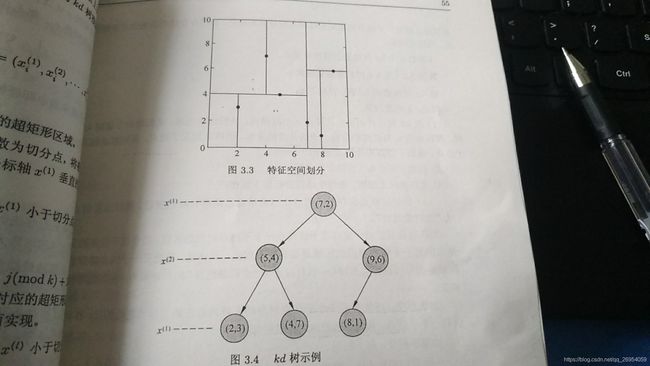
3.2利用例题3.2构造的kd树求点x=(3,4.5)^T的最近邻点。

x = (x0,x1)= (3,4.5)依照算法3.3步骤：

1.从根节点（7，2）比较x0值，将输入分在左边节点（5，4），即左边的矩形区域

2.在节点（5，4）比较x1的值，输入走右边，到叶节点（4，7）通过欧氏距离算距离2.69，记录“当前最近节点”（4，7），然后检查是否父节点的另外一个节点是否与目标点和“最近节点“距离的超球体相交；

.0

3.如果相交，进行最近邻搜索，计算（2，3）与目标点的距离1.802，距离更新记录，然后回退；如果不想交则直接回退父节点

同样的步骤，最后回退到根节点结束

最后答案为（2，3）为最近邻节点。

3.3参照算法3.3，写出输出为x的k近邻的算法

还是有bug的，不过比较小的k值不会有bug，太晚了，注释也懒得写那么详细

#-------------------------------------------------------------------------------
# Name:        k近邻算法
# Purpose:
#
# Author:      nkenen
#该算法比较简单实现k近邻算法
# Created:     29/03/2020
# Copyright:   (c) Administrator 2020
# Licence:     
#-------------------------------------------------------------------------------
import numpy as np
import matplotlib.pyplot as plt

class Node():
    def __init__(self,value=None,left=None,right=None,index=None,fnum=None):
        self.value = value#节点值
        self.left = left#左节点
        self.right = right#右节点
        self.index = index#xi的下标值
        self.fnum = fnum#树层


class KdTree():
    def __init__(self,X,k):
        self.fnode = None#根节点
        self.X = X#训练数据
        self.k = k
        self.xilen = len(X[0])
        self.mindistance = float("inf")#是最小近邻距离集最大的距离（懒得改名）
        self.mindistances = []#最小近邻距离集
        self.mindxs = []#最小节点集

    def createft(self):
        #找超平面，输出中间节点、左边节点集和右边节点集
        def findMd(Xin,index):
            if Xin.shape[0] <= 1:
                return (None,None,None)
            p = Xin
            p = p[np.lexsort(p[0:,:index+1:].T)]#先以当前节点集的xi排序
            mid = p[int(len(p)/2)]#找中间
            xl = p[0:int(len(p)/2)]#切出左边集
            xr = p[int(len(p)/2)+1:]#切出右边集
            return (mid,xl,xr)
        #递归创建树
        def create(fnde,Xin,index,fnum):
            index = index%self.xilen
            mid,xl,xr = findMd(Xin,index)
            #已经切分完毕
            if mid is None and len(Xin) == 1:
                fnde.value = Xin[0]
                fnde.index = None
            #还能切
            elif mid is not None:
                fnde.value = mid
                fnde.index = index
                #创左边节点
                fnde.left = Node(index=index,fnum = fnum)
                #递归切
                create(fnde.left,xl,index+1,fnum+1)
                #创右边节点
                fnde.right = Node(index=index,fnum = fnum)
                #递归切
                create(fnde.right,xr,index+1,fnum+1+1)

        self.fnode = Node()
        create(self.fnode,self.X,0,0)

    #前序打印树
    def preTraverse(self,node):
        if node == None:
            return
        print("it is node",node.value,node.index,node.fnum)
        self.preTraverse(node.left)
        self.preTraverse(node.right)

    #递归搜索遍历，不知道算不算
    def treesearch(self,x):
        #我直接遍历所有的节点，把距离最小的都加入了
        #只有最小的才可能是相邻的
        def findkmind(node,x,othernode):
            d = [[node.value,distance(node.value,x,2)],\
                [othernode.value,distance(othernode.value,x,2)]]
            for di in d:
                if len(self.mindistances) < self.k:
                    self.mindxs.append(di[0])
                    self.mindistances.append(di[1])
                else:
                    if di[1] x[node.index]:
                    search(node.left,x,node.right)
                else:
                    search(node.right,x,node.left)
            if node.value is not None and othernode is not None :
                findkmind(node,x,othernode)


        if len(x) != self.xilen:
            print("x input err")
            return
        search(self.fnode,x,self.fnode)
        print(self.mindistances,self.mindxs)


def main():
    p =np.array( [[2,3],
        [5,4],
        [9,6],
        [4,7],
        [8,1],
        [7,2]])
    #p =np.array([[i,j,m,n] for i in range(10) for j in range(10,1,-1) for m in range(10) for n in range(10)])
    ktree = KdTree(p,2)
    ktree.createft()
    ktree.preTraverse(ktree.fnode)
    #ktree.treesearch([3,4.5,1.5,5])
    ktree.treesearch([3,4.5])


    pass

if __name__ == '__main__':
    main()