离散数学---判断矩阵：自反性，反自反性，对称性得到矩阵的自反闭包，对称闭包。

目录

1-自反性，反自反性，对称性

2--矩阵的自反闭包，对称闭包

---

1-自反性，反自反性，对称性

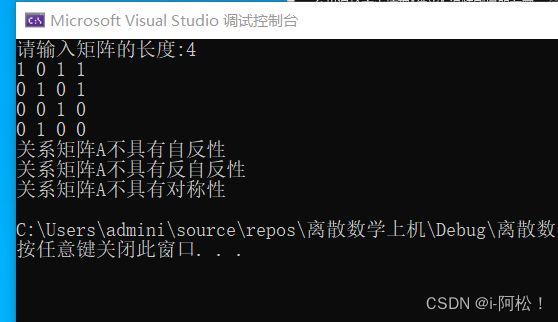
题目:从键盘输入集合A的元素值，键盘输入A到A 关系矩阵M。
判断该关系矩阵M是否具有
（1）自反性、
（2）反自反性、
（3）对称性、
输出以上各性质的判定结果。

    

 那么对于这个程序的执行，我们想法是什么？

• 创建一个二维数组，将1 0这样的元素储存进去
• 进行三次判断
• 如果if (i == j && arr1[i][j] == 1)是不是判断一次可以判断对角线都是1 即满足自反
• 如果if (i == j && arr1[i][j] == 0) 是不是判断一次可以判断对角线都是0 即满足反自反
• 如果 if (arr1[i][j] == arr1[j][i] == 1) 是不是可以判断满足对称性呢
• 这样想真的没错吗？ 停下来想一下
• 其实思路是没错的，但是整体还是不正确，因为你要判断对角线所有的元素都是1或者0，和那个所有的元素都是（i，j）对称的，所以这个时候你加一个m++，从0 开始，如若是的且满足 m = n（你输入矩阵的大小）那么其实是满足的

那么对于上述的分析可知，我们自然可可以设置三个函数，分别来对各个来进行判断，并且进行输出，记住我们是不需要返回值的void类型

void Reflexivity(int x, int y); //判断是否具有自反性

void Anti_reflexivity(int x, int y);//判断是否具有反自反性

void symmetry(int x, int y);//判断是是否具有对称性

然后利用for循环嵌套输入数值后就进行函数的调用

Reflexivity(n, n);//调用判断自反性的函数

     Anti_reflexivity(n, n);//调用判断反自反性的函数

     symmetry(n, n);//调用判断对称性的函数

 你这个时候可能疑问，为什么我没有把数组直接调用过去呢？

是因为我采用了全局数组的概念，反正这个是公共的大家都能用，反正三个函数大家都用的到，何乐而不为呢？

第一个是不用函数，直接进行定义的部分，如下：

#include
#define N 100 //使用宏定义给数组一个较大的值
int main()
{   
	int n, i, j, arr1[N][N];
	int flag1=0, flag2=0, flag3 = 0;
	int n1=0, n2=0;
	printf("请输入矩阵的长度:");
	scanf("%d", &n);//输入矩阵的长度，行列相同
	for (i = 0; i < n; i++)//循环行
	{
		for (j = 0; j < n; j++)//循环列
		{
			scanf("%d", &arr1[i][j]);//循环的目的就是元素的输入
		}
	}

	for (i = 0; i < n; i++)//同样是循环，但是是为了标注信息
	{
		for (j = 0; j < n; j++)//列循环
		{
			if (i == j&&arr1[i][j]==1){
				flag1 = 1;
				n1++;
			}	
			
			if (i == j && arr1[i][j] == 0) //要判断四次啊
			{
				flag2 = 1;
				n2++;
			}

			if (arr1[i][j] == arr1[j][i] == 1)//如果在二维数组中出现1
				flag2 = 1;
		}
	}
	
	if (flag1 == 1&&n1==4)
		printf("111\n");
	else
		printf("0000\n");

	if (flag2 == 1&&n2==4)
		printf("2222\n");
	else
		printf("3333\n");

	if (flag3 == 1)
		printf("444\n");
	else
		printf("5555\n");
}
//以上是离散数学的初级版本

一下是调用的其中的一个函数部分.

void Reflexivity(int x, int y) {
	int i, j, flag1=1,n1=0;
	for (i = 0; i < x; i++)//外层循环
	{
		for (j = 0; j < y; j++)//内层循环
		{
			if (i == j && arr1[i][j] == 1) {//对角线元素相等且为1
				flag1 = 1;
				n1++; //n的作用是判断是否每个对角线元素 1 都是存在的
			}
		}
	}
	if (flag1 == 1 && n1 == n)
		printf("关系矩阵A具有自反性\n");
	else
		printf("关系矩阵A不具有自反性\n");
}

整体的代码如下：（）

#include
#define N 100 
int arr1[N][N];
int n;
void Reflexivity(int x, int y); 
void Anti_reflexivity(int x, int y);
void symmetry(int x, int y);
int main()
{   
	int i, j;
	printf("请输入矩阵的长度:");
	scanf("%d", &n);
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n; j++)//循环列
		{
			scanf("%d", &arr1[i][j]);
		}
	}
	Reflexivity(n, n);
	Anti_reflexivity(n, n);
	symmetry(n, n);

}
void Reflexivity(int x, int y) {
	int i, j, flag1=1,n1=0;
	for (i = 0; i < x; i++)//外层循环
	{
		for (j = 0; j < y; j++)//内层循环
		{
			if (i == j && arr1[i][j] == 1) {
				flag1 = 1;
				n1++; 
			}
		}
	}
	if (flag1 == 1 && n1 == n)
		printf("关系矩阵A具有自反性\n");
	else
		printf("关系矩阵A不具有自反性\n");
}
void Anti_reflexivity(int x, int y) {
	int i, j, flag2=0, n2 = 0;
	for (i = 0; i < x; i++)//行（外）循环
	{
		for (j = 0; j < y; j++)//列（内）循环
		{
			if (i == j && arr1[i][j] == 0) {
				flag2 = 1;
				n2++; 
			}
		}
	}
	if (flag2 == 1 && n2 == n)
		printf("关系矩阵A具有反自反性\n");
	else
		printf("关系矩阵A不具有反自反性\n");
}
void symmetry(int x, int y) {
	int i, j, flag3=0,n3=0;
	for (i = 0; i < x; i++)
	{
		for (j = 0; j < y; j++)
		{
			if (arr1[i][j] == arr1[j][i] == 1)
			{
				flag3 = 1; 
				n3++;
			}
		}
	}
	if (flag3 == 1&& n3==n )
		printf("关系矩阵A具有对称性\n");
	else
		printf("关系矩阵A不具有对称性\n");
}

运行的效果： 

 

2--矩阵的自反闭包，对称闭包

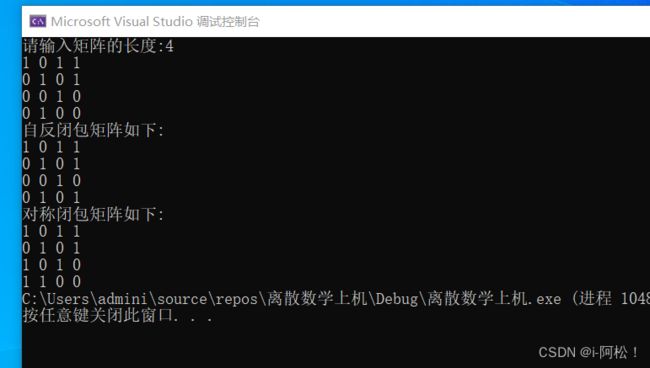
题目3：
从键盘输入集合A的元素值，键盘输入A
到A 关系矩阵M。
输出关系矩阵M的
（1）自反闭包矩阵、
（2）对称闭包矩阵

 

 则有关闭包，还有上面的那个图形，想一想你会定义几个二维数组呢？

三个第一个是为了存放初始的元素，也就是输入的元素，第二个数组和初始数组相加，如果二者之和大于1 那就是1 ，否则就是 0 ，不要说1 +1 =2 哈，第三个数组则是得到其转置。

• 创建三个二维数组，然后利用宏定义来给定义数组的长度
• 初始数组的数值的输入
• 进行二重循环来对数组2和数组3 进行处理
• 同样是二重循环来对其闭包的输出
• 结束.

这是核心代码：

for (i = 0; i < n; i++)//同样是循环，但是是为了标注信息

    {

         for (j = 0; j < n; j++)//列循环

         {

             if (i == j) arr2[i][j] = 1;//arr2为恒等关系

             else arr2[i][j] = arr1[i][j];//和数组1是一样

             if (arr1[i][j] == 1)//如果在二维数组中出现1

             {                  

                  arr3[i][j] = 1;//将其赋值为1

                  arr3[j][i] = 1;//那个数组3的转置矩阵

             }

         }

    }

整体代码的收尾工作：

#include
#define N 100 //使用宏定义给数组一个较大的值
int main()
{   
	int n, i, j, arr1[N][N], arr2[N][N], arr3[N][N] = { 0 };
	printf("请输入矩阵的长度:");
	scanf("%d", &n);
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n; j++)
		{
			scanf("%d", &arr1[i][j]);
		}
	}
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n; j++)
		{
			if (i == j) arr2[i][j] = 1;
			else arr2[i][j] = arr1[i][j];
			if (arr1[i][j] == 1)
			{                   
				arr3[i][j] = 1;
				arr3[j][i] = 1;
			}
		}
	}
	printf("自反闭包矩阵如下:\n");
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n; j++)
		{
			printf("%d ", arr2[i][j]);
		}
		printf("\n");
	}
	printf("对称闭包矩阵如下:\n");
	for (i = 0; i < n; i++)
	{
		for (j = 0; j < n; j++)
		{
			printf("%d ", arr3[i][j]);
		}
		if (i < n - 1) printf("\n");
	}
}

 运行的截图