深度学习基础——简单了解meta learning(来自李宏毅课程笔记)
知乎同名账号同步发布
目录
- 一、初步了解
- 二、和ML的差异
- 三、应用了解
一、初步了解
我们以分类问题为例,以前,学习的目的是学习一个二元分类器 f ∗ f^* f∗;现在,学习的目的是学习一个学习算法F,这个学习算法F能够学习一个二元分类器 f ∗ f^* f∗。
既然要直接学习一个学习算法F,那么就要考虑它的参数。以往的学习,是为了学习一个具体的二分类器 f ∗ f^* f∗,假设人为指定的学习算法是感知机,那么学习的过程需要改进的参数就是 w w w和 b b b。现在进行meta learning,目的是直接去学习学习算法F,那么需要关注的参数(上图中以“component”表示)就是网络架构、初始化参数、学习率等等,我们用 Φ \Phi Φ来表示这些参数, Φ \Phi Φ也被称为learnable components。
meta learning的训练过程,就是不断调整 Φ \Phi Φ,从而获得一个很好的学习算法F,然后在使用阶段中,用户就能用F去在给定的数据集上训练出一个二分类器 f ∗ f^* f∗,这个二分类器应该就是一个好的二分类器。
上图就是meta learning的一个总流程架构。具体而言,在以往的学习中,我们有一个训练集,有一个测试集,我们在训练集上利用感知机算法训练出一个loss比较低的二分类器,然后再在测试集上测试这个二分类器究竟好不好;而现在有了meta learning,情况就变了,我们有一个训练任务集(里面有一堆训练任务),有一个测试任务,每个训练任务中都有训练资料和测试资料,每个测试任务中都有训练资料和测试资料,我们利用这个训练任务集或者说这一堆训练任务来训练出一个很好的学习算法 F Φ ∗ F_{\Phi^*} FΦ∗,然后在测试阶段,用这个学习算法 F Φ ∗ F_{\Phi^*} FΦ∗在测试任务中的训练资料上来训练出一个二分类器 f θ ∗ f_{\theta^*} fθ∗,然后在测试任务中的测试资料上测试这个二分类器 f θ ∗ f_{\theta^*} fθ∗究竟好不好。
(当然,很显然的事情是,正如以往的学习中,测试数据不能在训练过程中出现一样,在meta learning中,训练过程不能使用测试任务。)
看到这你可能会有疑问,meta learning这样做,会不会有点画蛇添足了?为什么一定要先学习学习算法F,再用学习算法F来学习二分类器f呢?直接学习二分类器f不好吗?
实际上,在现实中,我们可能会面临一个问题,那就是数据的匮乏。还拿上述二分类问题作为例子,如果你要对猫和狗进行分类,那么labeled training data是非常多的,但是如果你要对长相别致的奇珍异兽——比如非洲穿山甲和鬃狼进行分类,而你只有少量的labeled training data,那么此时要怎么做呢?先说答案:此时你的做法可以是,找一大堆训练任务,这些任务中可以有猫狗二分类任务、苹果橘子二分类任务、汽车自行车二分类任务等等,总之这些任务的labeled data非常充裕,然后你把这些二分类任务作为meta learning的训练任务,去训练一个二分类学习算法F,然后再将非洲穿山甲和鬃狼的二分类任务作为测试任务,你可能只能为这个测试任务收集到少量的labeled data,即这个训练任务的训练资料和测试资料都比较少,但是由于你已经有了一个不错的F,那么你就可以用F在这少量的训练资料上训练出一个非洲穿山甲和鬃狼的二分类器(然后再在测试资料上去测试这个二分类器)。
接下来,我进一步来阐述一下上面这个过程的合理性,即我们用容易搜集的数据去训练F,然后用F在不容易搜集的数据上训练f,为什么这个f就可能是有效的?我们从人自身的成长来入手分析这个问题,试想一下,在你能够分辨电脑和手机的区别前,你大概率只见过几部手机、几部电脑,但是你就能够成功分辨出电脑和手机的区别。似乎,你把自己训练成“电脑手机二分类器”前,也并没有接触多少训练资料,那么为什么你就能够获得成功呢?实际上,那是因为你在之前的生活中就积累了大量的经验,可能在你上小学中学的时候,你见过白板和黑板的区别,于是你明白了物体可以用颜色来区分;可能你吃过汤圆和雪汤圆(一种雪糕),虽然两者长得很像,但你明白了物体可以用温度来区分;可能你在生活中遇到过无数种圆形和方形的物体,所以你明白了形状也是区分物体的重要参考信息…总之在你接触到手机和电脑之前,你可能已经在无数的二分类问题上训练过自己,换句话说,你已经接触到了巨量的二分类训练任务的训练资料,学习出了一个二分类问题的学习算法F。那么现在,当你第一次接触到电脑和手机,思考它们之间的区别的时候,你就启动了用F在少量的电脑、手机训练资料上训练电脑-手机二分类器的过程,从而轻而易举地获得了一个不错的电脑-手机二分类器f。
形象的说法就说到这里,接下来还是回到meta learning这项技术本身。
再看一遍上面图片中的流程架构,我们说过,F是依靠一堆训练任务训练出来的,但是没有讲训练过程要怎么做。我们知道每个训练任务中都有训练资料和测试资料,你可能会问,刚才提到了测试任务中的训练资料和测试资料应该如何使用,但是还没有讲训练任务中的训练资料和测试资料如何使用,那么应该如何使用呢?如何利用这一堆训练任务中的训练资料训练出这个学习算法 F Φ ∗ F_{\Phi^*} FΦ∗呢?这一堆训练任务中的测试资料是干什么用的呢?我们要怎么像往常一样去计算这个loss呢?即便是有了loss,如何去优化learnable components Φ \Phi Φ呢?
接下来回答这个问题:
上图给出了一个训练过程。假设,训练任务集中有两个任务,任务一是苹果橘子二分类任务,任务二是自行车汽车二分类任务。任务一有一些苹果橘子照片当做训练资料,有一些苹果橘子照片当做测试资料;任务二有一些自行车汽车照片当做训练资料,有一些自行车汽车照片当做测试资料。

和传统的学习一样,一开始我们要初始化learnable component Φ \Phi Φ,从而我们有一个初始的学习算法 F Φ F_\Phi FΦ。
我们先针对任务一做一些事情,要做的事情就是使用 F Φ F_\Phi FΦ在其中的训练资料(一部分苹果橘子照片)上来训练一个二分类器 f θ 1 ∗ f_{\theta^{1*}} fθ1∗,这个 θ 1 ∗ \theta^{1*} θ1∗就特指利用 F Φ F_\Phi FΦ在任务一上学习的二分类器 f θ 1 ∗ f_{\theta^{1*}} fθ1∗的参数。
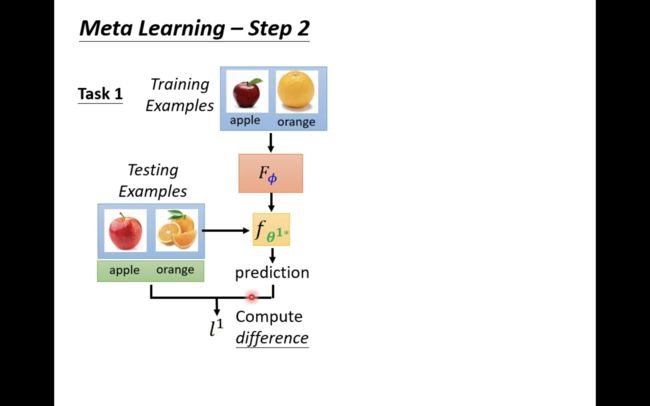
然后,用这个二分类器去对任务一的测试资料进行测试,从而计算出一个loss l 1 l^1 l1;
同样地,我们也可以对任务二把上述流程重复一遍,从而得到loss l 2 l^2 l2:
最终的loss自然就等于 l 1 + l 2 l^1+l^2 l1+l2
当然,如果训练任务集中有N个任务,那么最终的loss就如下图中所示那样:
现在有了loss,自然就可以进行优化了,如下图:
上图的过程就和传统的学习过程非常相像了。但是还有个问题,我们知道在感知机算法中,你可以直接让loss对 w w w和 b b b算梯度,然后使用梯度下降,但是在meta learning中我们的参数是learnable component Φ \Phi Φ,它包含了网络的架构等等离散的、在loss中不可微的元素,那要怎么优化呢?李宏毅表示,如果你能够计算loss对 Φ \Phi Φ的微分,那么就可以使用梯度下降,如果不能,则可以使用Reinforcement Learning或者Evolutionary Algorithm。
二、和ML的差异
到这里,meta learning的基本思想流程都清楚了,接下来比较一下meta learning和machine learning之间的差异:
首先,是上图,一个是找f,一个是找F,F是用来找f的。
其次,ML对应一个任务,meta learning对应多个任务。注意任务中的训练资料也被称为Support set,测试资料也被称为Query set。meta learning的学习过程被称为Across-task Training。
上图有Within-task和Across-task的对比,意义自明。
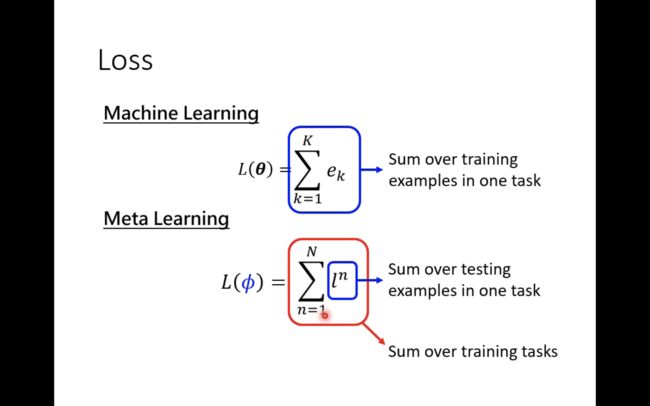
当然两者之间的loss也是有区别的。

ML中的技术或者事情,也都可以用在或者发生在meta learning上。其中上述development task对应的是“验证任务”,它介于训练任务和测试任务之间,可以视为对应ML中的验证集。
三、应用了解
接下来说说不同种类的meta learning。
meta learning是怎么分类的呢?我们最早提过, Φ \Phi Φ代表的是meta learning中的参数,它叫learnable components,它里面有很多component,可能包含网络架构、参数初始化、学习率等等。当然这些component可能有、也可能没有,所以我们将不同的 Φ \Phi Φ对应到不同种类的meta learning上:

比如说,如果 Φ \Phi Φ指的就是网络架构,那么meta learning就变成了很多人耳熟能详的NAS:
那么此时loss对 Φ \Phi Φ肯定就是不可微的,就可以使用强化学习等技术:
当然除了强化学习,也可以使用进化算法,上图给出了一些相关的paper。
meta learning还有一些应用,比如Few-shot Image Classification:
先记这么多,李宏毅还有一节课,那节课讲的就是更具体的算法细节了,今天先了解meta learning基本思想,需要的时候再看吧。