强化学习-从Q-Learning到DQN(Deep Q-Network)

强化学习-从Q-Learning到DQN(Deep Q-Network)

强化学习是一种从环境状态映射到动作的学习，目标是使agent在与环境environment交互过程中获得最大的累积奖赏。
这个过程可以解释为，在时刻t，智能体agent基于当前环境的状态state，做出动作action，然后这个动作作用到当前环境所处的状态后，返回给智能体agent一个奖赏reward，接着智能体agent进入了时刻t+1的状态。

智能体（agent）、环境状态（environment）、奖励（reward）、动作（action）可以将问题抽象成一个马尔科夫决策过程。

Q-Learning

Q-Learning是强化学习中的经典算法，主要依赖Q表存储State（状态）和Action（动作），根据Q值选取最大收益的动作。
Q表用于记录状态-动作对的值，初始化格式见下表。

	action1	action2	action3	…
state1	q(state1, action1)	q(state1, action2)	q(state1, action3)
state2	q(state2, action1)	q(state2, action2)	q(state2, action3)
state3	q(state3, action1)	q(state3, action2)	q(state3, action3)
…

Q表的更新公式如下，其中$\alpha$为学习率, $\gamma$为奖励性衰变系数，r为a动作的奖励
$$Q(s,a)\leftarrow Q(s,a)+\alpha [r+\gamma ma{x}_{a^{\prime }}Q(s^{\prime },a^{\prime })-Q(s,a)].$$
根据过往Q表里面的Q(s,a)作为Q估计， 根据下一个状态s’中选取最大的Q (s′,a′) 乘以衰变系数 $\gamma$加上真实回报值作为为Q现实。
为了验证Q-Learning的更新过程，引用了一位知乎大佬的例子。
知乎链接

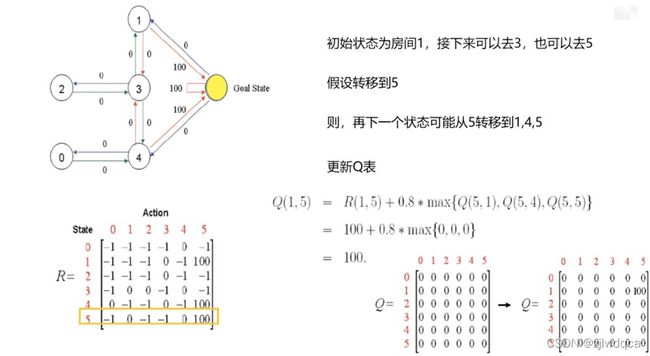
现有一个5房间的房子，如下图所示，房间与房间之间通过门连接，编号0到4,5号是房子外边，即我们的终点。我们将agent随机放在任一房间内，每打开一个房门返回一个reward。

下图为房间之间的抽象关系图，箭头表示agent可以从该房间转移到与之相连的房间，箭头上的数字代表reward值。

因此，可以得到下面的回报矩阵

   [[-1,-1,-1,-1,0,-1],
   [-1,-1,-1,0,-1,100],
   [-1,-1,-1,0,-1,-1],
   [-1,0, 0, -1,0,-1],
   [0,-1,-1,0,-1,100],
   [-1,0,-1,-1,0,100]]

设置学习率$\alpha$=1, 奖励性衰变系数$\gamma$为0.8，更新过程见下图。

python代码

import numpy as np
GAMMA = 0.8
Q = np.zeros((6, 6))
# 初始矩阵
R=np.asarray(
   [[-1,-1,-1,-1,0,-1],
   [-1,-1,-1,0,-1,100],
   [-1,-1,-1,0,-1,-1],
   [-1,0, 0, -1,0,-1],
   [0,-1,-1,0,-1,100],
   [-1,0,-1,-1,0,100]]
)

def getMaxQ(state):
    return max(Q[state, :])
def QLearning(state):
    curAction = None
    for action in range(6):
        if(R[state][action] == -1):
            Q[state, action] = 0
        else:
            curAction = action
            Q[state, action] = R[state][action] + GAMMA * getMaxQ(curAction)
count=0
while count < 1000:
    for i in range(6):
        QLearning(i)
    count += 1
print(Q)

最终Q表矩阵为

Q表矩阵的最大值为什么是500呢？
这是由于我们设置了学习率$\alpha$=1, 奖励性衰变系数$\gamma$为0.8的原因，当我们选中state=5, action=5时，即对Q[5, 5]进行更新时，Q[5, 5] = R[5][5] + 0.8 * max{Q[5, 1], Q[5, 4], Q[5, 5]} = 500，因此Q表中最大值只能是500。
当我们将奖励性衰变系数$\gamma$改为为0.6，得到最终的Q表矩阵为

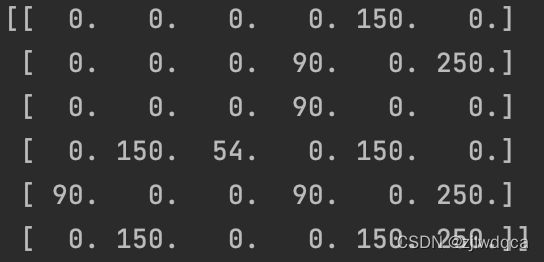
Q-Learning方法可以解决状态空间和动作空间都很小的问题，对于巨大状态空间和动作空间的问题，创建一个Q表的内存开销是非常大的，除此以外，数据量和时间开销的限制也是Q-Learning算法的一个缺陷。

DQN(Deep Q-Network)

DQN（Deep Q-Network）是将深度学习与强化学习相结合，实现了从感知到动作的端到端的革命性算法。当我们的Q表过于庞大无法建立的话，使用DQN是一种很好的选择。

在介绍DQN(Deep Q-Network)之前先了解一下值函数近似（Function Approximation）方法。
值函数近似方法是为了解决状态空间过大，也称为“维度灾难”的问题。通过一个非线性或者线性的函数替代Q表去存储状态和动作，也可以将其看作是一个拟合$\omega$权重的过程。
$$\hat{v}(s,\omega )\approx v_{\pi }(s)or\hat{q}(s,a,\omega )\approx q_{\pi }(s,a)$$

DQN作为一种深度强化学习模型，将卷积神经网络与传统强化学习中的Q-Learning算法相结合，将Q-Learning的Q表变成了Q-Network, 把输入的状态提取特征作为输入，通过MC/TD计算出值函数作为输出，然后对函数参数w权重进行训练，直到模型收敛。

训练样本的采集主要通过$\epsilon -greedy$策略生成,一般前几个episode都用来生成样本，后边的episode才进行模型训练。即采用批处理法，先攒出一部分样本，再从其中采样一部分拿来更新Q网络，这种方法又称为经验回放，使用这种方式可以解决强化学习采集样本关联性的问题，打破数据间的关联，从而可以提高算法的稳定性。
模型的损失函数用真实Q值和模拟Q值的均方差计算。

$$q_{\pi }(s,a)=r+\gamma ma{x}_{a^{\prime }}q(s^{\prime },a^{\prime },\omega )$$s’为下一时刻状态
$$J(\omega )=E_{\pi }[(q_{\pi }(s,a)-\hat{q}(s,a,\omega ){)}^2]$$

DQN训练过程见下图

python代码

"""
Dependencies:
torch: 0.4
gym: 0.8.1
numpy
"""
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import gym
import pickle

# Hyper Parameters
BATCH_SIZE = 32
LR = 0.01                   # learning rate
EPSILON = 0.9               # greedy policy
GAMMA = 0.9                 # reward discount
TARGET_REPLACE_ITER = 100   # target update frequency
# 记忆行数
MEMORY_CAPACITY = 2000
# 引入gym的CartPole环境
env = gym.make('CartPole-v0')
env = env.unwrapped

# 得到状态
# 2
N_ACTIONS = env.action_space.n
# 4
N_STATES = env.observation_space.shape[0]
ENV_A_SHAPE = 0 if isinstance(env.action_space.sample(), int) else env.action_space.sample().shape     # to confirm the shape



# 神经网络
class Net(nn.Module):
    def __init__(self, ):
        super(Net, self).__init__()
        # 输入观测值
        self.fc1 = nn.Linear(N_STATES, 50)
        # 利用二次分布生成初始权值
        self.fc1.weight.data.normal_(0, 0.1)   # initialization
        # 输出每个动作的价值
        self.out = nn.Linear(50, N_ACTIONS)
        self.out.weight.data.normal_(0, 0.1)   # initialization

    def forward(self, x):
        x = self.fc1(x)
        x = F.relu(x)
        # 返回每个动作的价值
        actions_value = self.out(x)
        return actions_value

# DQN网络
class DQN(object):
    def __init__(self):
        # 参数不同的相同网络，eval的参数每次都在更新 总是快target好几个版本
        self.eval_net, self.target_net = Net(), Net()
        # 记录学习到多少步
        self.learn_step_counter = 0                                     # for target updating
        # 记忆库位置
        self.memory_counter = 0                                         # for storing memory
        # 初始化记忆库 s, a, r, s_
        self.memory = np.zeros((MEMORY_CAPACITY, N_STATES * 2 + 2))     # initialize memory
        self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=LR)
        self.loss_func = nn.MSELoss()
    # 采取动作
    def choose_action(self, x):
        x = torch.unsqueeze(torch.FloatTensor(x), 0)
        # input only one sample
        # 随机选取概率
        if np.random.uniform() < EPSILON:   # greedy 选取最大价值的动作
            actions_value = self.eval_net.forward(x)
            action = torch.max(actions_value, 1)[1].data.numpy()
            action = action[0] if ENV_A_SHAPE == 0 else action.reshape(ENV_A_SHAPE)  # return the argmax index
        else:   # random
            action = np.random.randint(0, N_ACTIONS)
            action = action if ENV_A_SHAPE == 0 else action.reshape(ENV_A_SHAPE)
        return action
    # 存储记忆
    def store_transition(self, s, a, r, s_):
        transition = np.hstack((s, [a, r], s_))
        # replace the old memory with new memory
        # 如果记忆存满了，覆盖掉老的记忆
        index = self.memory_counter % MEMORY_CAPACITY
        self.memory[index, :] = transition
        self.memory_counter += 1
    # 记忆库中提取学习
    def learn(self):
        # target parameter update
        # 每100个learn_step_counter才更新下target_net
        if self.learn_step_counter % TARGET_REPLACE_ITER == 0:
            self.target_net.load_state_dict(self.eval_net.state_dict())
        self.learn_step_counter += 1

        # sample batch transitions
        # 随机抽取记忆
        sample_index = np.random.choice(MEMORY_CAPACITY, BATCH_SIZE)
        # 把记忆对应的项都取出来
        b_memory = self.memory[sample_index, :]
        b_s = torch.FloatTensor(b_memory[:, :N_STATES])
        b_a = torch.LongTensor(b_memory[:, N_STATES:N_STATES+1].astype(int))
        b_r = torch.FloatTensor(b_memory[:, N_STATES+1:N_STATES+2])
        b_s_ = torch.FloatTensor(b_memory[:, -N_STATES:])

        # q_eval w.r.t the action in experience
        # 选取当时状态施加动作的价值
        q_eval = self.eval_net(b_s).gather(1, b_a)  # shape (batch, 1)
        # 下一个状态的价值， 加上detach让target网络不更新，因为target的参数是通过TARGET_REPLACE_ITER来更新的
        q_next = self.target_net(b_s_).detach()     # detach from graph, don't backpropagate
        # 利用当前动作奖励和未来状态计算target值
        q_target = b_r + GAMMA * q_next.max(1)[0].view(BATCH_SIZE, 1)   # shape (batch, 1)
        # 计算真实值和估计值的差距
        loss = self.loss_func(q_eval, q_target)

        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

dqn = DQN()
print('\nCollecting experience...')

ep_r_list = []
for i_episode in range(400):
    # 根据现在所处的环境得到一个反馈
    s = env.reset()
    # print("state", s)
    ep_r = 0
    while True:
        # 环境渲染
        env.render()
        # 根据状态 选择动作 0或1，左右摇摆
        a = dqn.choose_action(s)
        # print("action", a)
        # take action
        # 环境采取行动得到的反馈 s_下一个状态 r 回报 done是否结束这一轮 info 不知道干啥的
        s_, r, done, info = env.step(a)
        # print("s_", s_)
        # print("r", r)
        # print("done", done)
        # print("info", info)

        # 计算奖励
        # modify the reward
        x, x_dot, theta, theta_dot = s_
        # 代表杆子立的越直越好
        r1 = (env.x_threshold - abs(x)) / env.x_threshold - 0.8
        # 代表小车的位置越靠中间越好
        r2 = (env.theta_threshold_radians - abs(theta)) / env.theta_threshold_radians - 0.5
        r = r1 + r2

        # print("r", r)
        # 存储反馈
        dqn.store_transition(s, a, r, s_)
        ep_r += r
        # 如果存满了
        if dqn.memory_counter > MEMORY_CAPACITY:
            dqn.learn()
            if done:
                print('Ep: ', i_episode,
                      '| Ep_r: ', round(ep_r, 2))
                ep_r_list.append((i_episode, round(ep_r, 2)))
        if done:
            break
        # 现在的状态变到下一个状态
        s = s_

with open('ep_r.pkl', 'wb') as f:
    pickle.dump(ep_r_list, f)

使用平均得分作为评价指标。测试性能时agent进行一定的步数执行，记录agent所获得的所有奖励值并对其求平均。

参考了下面几篇大佬的博客和教程

https://zhuanlan.zhihu.com/p/35882937
https://blog.csdn.net/qq_30615903/article/details/80744083
https://www.bilibili.com/video/BV1Vx411j7kT?p=27