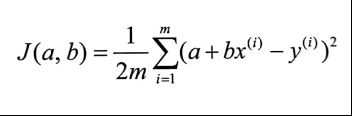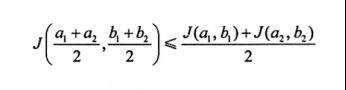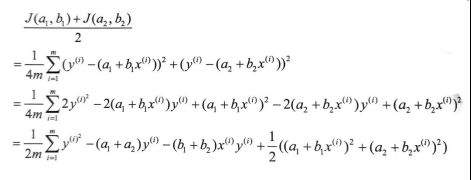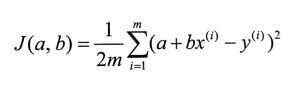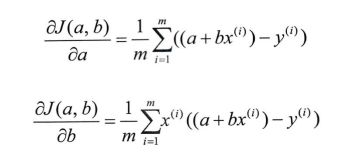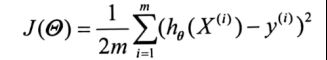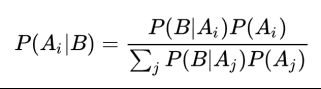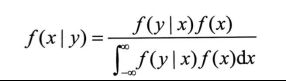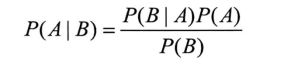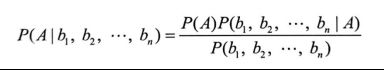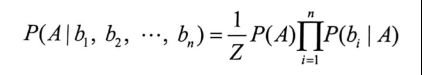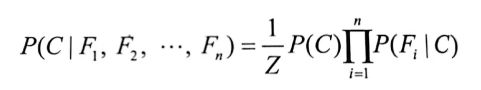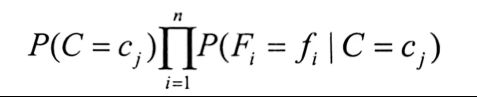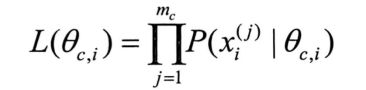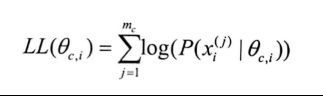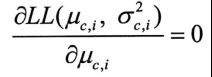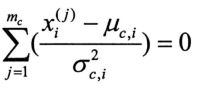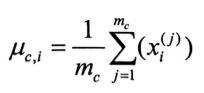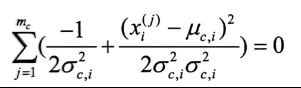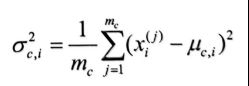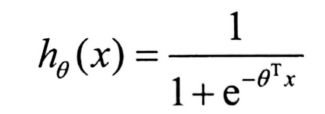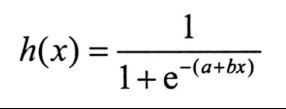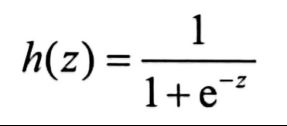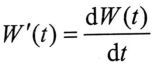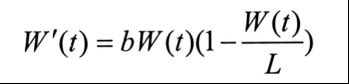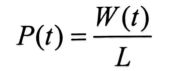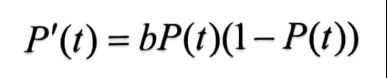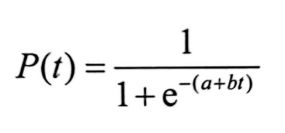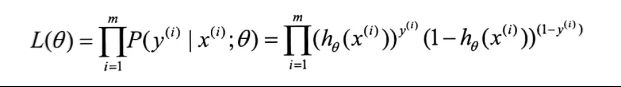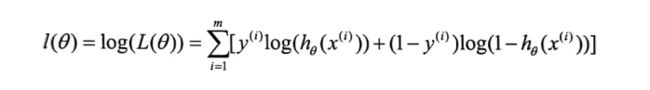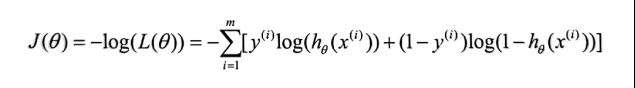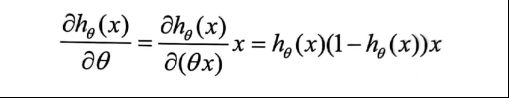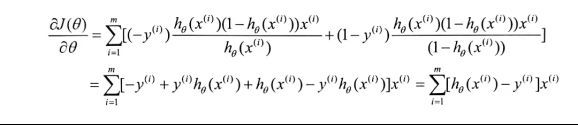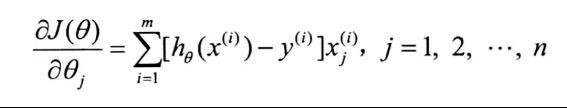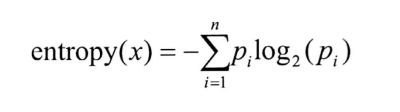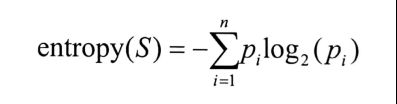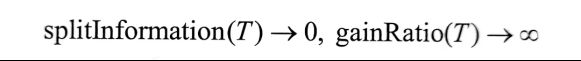机器学习极简入门笔记-2-有监督学习基础

目录

第8章 线性回归

8.1 代价函数

8.2 使用梯度下降法求解目标函数

8.3 多维情形

8.4 线性回归的超参数

8.5 线性回归程序

第9章 朴素贝叶斯分类器

9.1 分类与回归

9.2 贝叶斯定理

9.3 朴素贝叶斯算法

9.4 朴素贝叶斯分类器

9.5 条件概率的参数

 9.5.1 极大似然估计

 9.5.2 正态分布的极大似然估计

9.6 朴素贝叶斯分类器程序

第10章 逻辑回归

10.1 Sigmoid函数

10.2 非线性逻辑回归函数的由来

10.2.1 指数增长

10.2.2 逻辑函数

10.3 回归模型

10.3.1 模型函数

10.3.2 目标函数

10.4 代码实现

10.5 多分类问题

第11章 决策树

 11.1 什么是决策树

 11.2 几种常用算法

11.2.1 ID3

11.2.2 C4.5

11.2.3 CART

 11.3 剪枝优化

11.4 代码实现

---

• 第8章 线性回归

8.1 代价函数

现证明此代价函数是凸函数。可证明

证明过程如下

---

8.2 使用梯度下降法求解目标函数

分别对a、b求偏导，得到

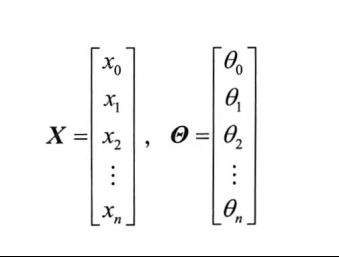
8.3 多维情形

此时模型函数为

目标函数为

---

8.4 线性回归的超参数

对于线性回归而言，只要用到梯度下降法，就会有步长超参数 a。

如果训练结果偏差较大，可以尝试调小步长

如果模型质量不错但是训练效率太低，可以适当放大步长

此外也可以尝试使用动态步长:开始步长较大，随着梯度的缩小，步长同样缩小。

• 如果训练程序是通过人工指定迭代次数来确定退出条件，则迭代次数也是一个超参数。
• 如果训练程序以模型结果与真实结果的整体差值小于某一个阈值为退出条件，则这个阈值就是超参数。

在模型类型和训练数据确定的情况下，超参数的设置成了影响模型最终质量的关键。一个模型往往会涉及多个超参数，如何制定策略在最少尝试的情况下让所有超参数设置的结果达到最佳，是一个在实践中非常重要又没有“银弹”的问题。

在实际应用中，能够在调参方面有章法，而不是乱试一气，有赖于大家对于模型原理和数据的掌握。

---

8.5 线性回归程序

这里使用sklearn库

import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model

experiences = np.array([0,1,2,3,4,5,6,7,8,9,10])
salaries = np.array([103100, 104900, 106800, 108700, 110400, 112300, 114200, 116100, 117800, 119700, 121600])

# 将特征数据集分为训练集和测试集，除了最后4个作为测试用例，其他都用于训练
X_train = experiences[:7]
X_train = X_train.reshape(-1,1)
X_test = experiences[7:]
X_test = X_test.reshape(-1,1)

# 把目标数据（特征对应的真实值）也分为训练集和测试集
y_train = salaries[:7]
y_test = salaries[7:]

# 创建线性回归模型
regr = linear_model.LinearRegression()

# 用训练集训练模型
regr.fit(X_train, y_train)

# 用训练得出的模型进行预测
diabetes_y_pred = regr.predict(X_test)

# 将测试结果以图标的方式显示出来
plt.scatter(X_test, y_test, color='black')
plt.plot(X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

 运行结果如下图

---

 

• 第9章 朴素贝叶斯分类器

9.1 分类与回归

分类模型与回归模型最根本的不同在于前者是预测一个标签(类型、类别)，后者则是预测一个数值。换一个角度来看，分类模型输出的预测值是离散值，而回归模型输出的预测值是连续值。也就是说，给模型输入一个样本，回归模型给出的预测结果是在某个值域(一般是实数或其子集)上的任意值，而分类模型则是给出特定的某几个离散值之一。

---

9.2 贝叶斯定理

---

9.3 朴素贝叶斯算法

在此式子中，假设影响B的因素有n个，则P(A|B)可以写为

 

假设bi相互独立，我们设Z=P(b1，b2，...，bn)，可以得到

---

9.4 朴素贝叶斯分类器

我们将之前得到的结果换一个写法

其中，Fi表示样本的第i个特征，C为类别标签

这个公式即为朴素贝叶斯分类器的模型函数

使用其预测的流程如下

假设有一个朴素贝叶斯分类器，能够区分k个类别{c1，c2，...，ck}，用来分类的特征有n个{F1，F2，...，Fn}

现有一个样本s，提取其所有特征值f1到fn，代入如下式子进行k次运算

比较这k次的结果，结果的值最大的时候对应的cj即是类别的预测值

---

9.5 条件概率的参数

对于P(Fi|C)的计算，我们可以通过该特征在数据样本中的分布来计算该特征的条件概率

统计学界有两个学派:频率学派和贝叶斯学派。这两个学派对于最基本的问题，即世界的本质是什么样的，看法不同。

频率学派认为:世界是确定的，有一个本体，这个本体的真值不变。我们的目标就是要找到这个真值或真值所在的范围。具体到“求正态分布的参数值”问题，他们认为:这两个参数虽然未知，但是在客观上存在固定值，我们要做的是通过某种准则，根据观察数据(训练数据)把这些参数值确定下来。

贝叶斯学派认为:世界是不确定的，本体没有确定真值，真值符合一个概率分布。我们的目标是找到最优的、可以用来描达述本体的概率分布。具体到“求正态分布的参数值”问题，他们认为:这两个参数 (均值和方差)，本身也是变量，也符合某个分布。因此，可以假定参数服从一个先验分布，然后再基于观察数据(训练数据)来计算参数的后验分布。

这里我们讲的是朴素贝叶斯模型，那到了需要估计条件概率参数的时候，应该是用贝叶斯学派的方法吗?还真不是!我们会选取频率学派的做法：极大似然估计法

9.5.1 极大似然估计

似然，它指某一种事件发生的可能性，和概率相似。

二者的区别在于:概率是在已知参数的情况下 预测后续观测所得到的结果;似然则正相反，用于参数未知但某些观测所得结果已知的情况下，对参数进行估计。

 

极大似然估计，就是去寻找让似然函数的取值达到最大的参数值的估计方法

为了便于计算，对上式取对数，得到对数似然函数

最大化一个似然函数，同最大化它的自然对数是等价的

因为自然对数log是一个连续且在似然函数的值域内严格递增的上凸函数，所以我们可以参考前面线性回归目标函数的求解办法，对似然函数求导，然后在设定导函数为0的情况下，求取该函数的最大值。

注意，自然对数是以常数e为底的对数，常表示为lnx或logx。这里采用机器学习中常用的表示方法logx来表示自然对数。

 9.5.2 正态分布的极大似然估计

其中

对μ求偏导，得到

令

则

即

下面对σ²求偏导

令

得到

这样我们就估算出了第i个特征正态分布的两个参数，第i个特征的具体分布也就确定下来了

---

9.6 朴素贝叶斯分类器程序

import pandas as pd
import numpy as np
import time
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB

# 导入数据集
# 数据文件详见代码后面
data = pd.read_csv("career_data.csv")

# 将分类变量转换为数值型
data["985_cleaned"]=np.where(data["985"]=="Yes",1,0)
data["education_cleaned"]=np.where(data["education"]=="bachlor",1, np.where(data["education"]=="master",2,np.where(data["education"]=="phd",3,4)))
data["skill_cleaned"]=np.where(data["skill"]=="c++",1,np.where(data["skill"]=="java",2,3))
data["enrolled_cleaned"]=np.where(data["enrolled"]=="Yes",1,0)

# 将数据集分为训练集和测试集
X_train, X_test = train_test_split(data, test_size=0.1, random_state=int(time.time()))

# 初始化分类器
gnb = GaussianNB()
used_features =[
"985_cleaned",
"education_cleaned",
"skill_cleaned"
]

# 训练分类器
gnb.fit(X_train[used_features].values,X_train["enrolled_cleaned"])
y_pred = gnb.predict(X_test[used_features])

# 打印结果
print("Number of mislabeled points out of a total {} points : {}, performance {:05.2f}%".format(
    X_test.shape[0],
    (X_test["enrolled_cleaned"] != y_pred).sum(),
    100*(1-(X_test["enrolled_cleaned"] != y_pred).sum()/X_test.shape[0])
    ))

 career_data.csv内容如下

no	985	education	skill	enrolled
1	Yes	bachlor	C++	No
2	Yes	bachlor	Java	Yes
3	No	master	Java	Yes
4	No	master	C++	No
5	Yes	bachlor	Java	Yes
6	No	master	C++	No
7	Yes	master	Java	Yes
8	Yes	phd	C++	Yes
9	No	phd	Java	Yes
10	No	bachlor	Java	No

---

• 第10章 逻辑回归

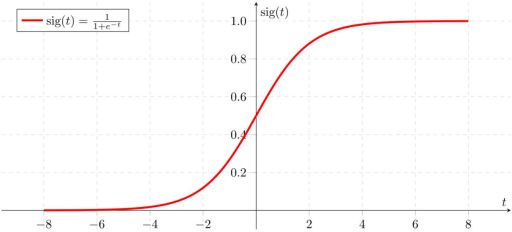
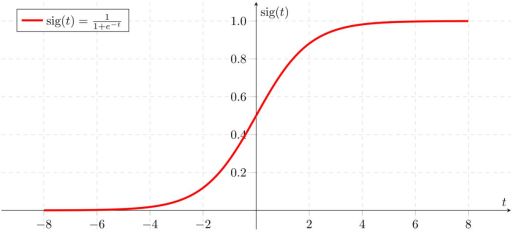
10.1 Sigmoid函数

具体形式如下

如果自变量为一元，则为如下形式

令z=a+bx，得到

---

10.2 非线性逻辑回归函数的由来

10.2.1 指数增长

最初，学者们将人口或化合物数量与时间的函数定义为W(t)，其中自变量t表示时间， W(t)表示人口或化合物数量。W(t)表示的是存量，则W(t)对t求微分的结果W’(t)就代表了人口或化合物的增长率，因此增长率函数为:

最简单的假设是W’(t)与W(t)成正比，即W’(t)=bW(t)

根据指数函数的求导特性，不妨将指数函数引入其中，得到

马尔萨斯人口论中“在没有任何外界阻碍的情况下，人口将以几何级数增长”的说法正是依据这样一个模型

10.2.2 逻辑函数

19世纪早期，开始有数学家、统计学家质疑指数增长模型，因为任何事物如果真的按照几何级数任意增长下去，都会达到不可思议的数量。

但是根据我们的经验，在自然界中，并没有什么东西是在毫无休止地增长的。当一种东西的数量越来越多时，某种阻力也会越来越明显地抑制其增长。

比利时数学家Verhulst给出了一个新的模型:

W’(t)=bW(t)-g(W(t))

其中，g(W(t))是以W(t)为自变量的函数，它代表随着总数增长出现的阻力

Verhulst 实验了几种不同形式的阻力函数，当阻力函数表现为W(t)的二次形式时，新模型显示出了它的逻辑性。

因此，新模型的形式可以表示为:

令

 

 得到

解此微分方程，即可得到

这便是Sigmoid函数的由来

Sigmoid函数的导函数被称为逻辑分布函数

---

10.3 回归模型

10.3.1 模型函数

一般而言，当y>0.5 时，z 被归类为真(true)或阳性(positive)，当y≤0.5时，z被归类为假(false)或阴性(negative)。

所以，在模型输出预测结果时，不必输出y的具体取值，而是根据上述判别标准输出1(真)或0(假)。因此，逻辑回归的典型应用是二分类问题。

10.3.2 目标函数

而从公式本身的角度来看，h(x)实际上是x为阳性的分布概率，所以才会在h(x)>0.5时将x归于阳性。也就是说，h(x)=P(y=1)。反之，样例是阴性的概率P(y=0)=1-h(x)。

当我们把测试数据代入其中的时候，P(y=1)和1(y=0)就有了先决条件，它们为训练数据的x所限定。因此:

• P(y=1|x)=h(x)
• P(y=0|x)=1-h(x)

由二项分布公式，得到

假设我们的训练集一共有m个数据，那么这m个数据的联合概率为

其对数似然函数为

为了将其变成凸函数，我们对上面式子整体加一个负号，得到其负对数似然函数

这就是逻辑回归的目标函数

10.3.3 梯度下降法

根据Sigmoid函数的求导特点，我们有

 因此我们得到

x为n维时，θ也为n维，此时

---

10.4 代码实现

from sklearn.linear_model import LogisticRegression
import pandas as pd

# 导入数据集
data = pd.read_csv('quiz.csv', delimiter=',')
used_features = ["Last Score", "Hours Spent"]
X = data[used_features].values
scores = data["Score"].values
X_train = X[:11]
X_test = X[11:]

# 逻辑回归——二分类法
passed = []
for i in range(len(scores)):
    if(scores[i] >= 60):
        passed.append(1)
    else:
        passed.append(0)

y_train = passed[:11]
y_test = passed[11:]
classifier = LogisticRegression(C=1e5)
classifier.fit(X_train, y_train)
y_predict = classifier.predict(X_test)
print(y_predict)

数据文件在下一节末尾

输出：

[1 0 1]

---

10.5 多分类问题

逻辑回归一般是用来做二分类的，但是如果我们面对的是多分类问题，比如样本标签的枚举值多于两个，还能用逻辑回归吗?当然可以，此时可以把二分类问题分成多次来做

假设有n个标签(类别)，也就是说可能的分类一共有n个，此时就可以构个逻辑回归分类模型，第一个模型用来区分 label_1 和non-labe1_1(即所有不属 labe1_1 的都归属到一类)，第二个模型用来区分 label_2 和 non-label_2……第n个模型用来区分 label_n 和non-label_n。

使用的时候，每一个输入数据都被这n个模型同时预测。最后哪个模型得出了阳性结果，就是该数据最终的结果。

如果有多个模型得出了阳性结果，那也没有关系。因为逻辑回归是一个回归模型，所以它直接预测的输出不仅是一个标签，还包括该标签正确的概率。对比几个阳性结果的概率，选最高的那个。

例如，对于某个数据，第一个模型和第二个模型都给出了阳性结果，不过 label_1模型的预测值是0.95，而label_2 的结果是 0.78，此时选高的，结果就是 label_1。

代码如下

from sklearn.linear_model import LogisticRegression
import pandas as pd

# 导入数据集
data = pd.read_csv('quiz.csv', delimiter=',')
used_features = [ "Last Score", "Hours Spent"]
X = data[used_features].values
scores = data["Score"].values
X_train = X[:11]
X_test = X[11:]

# 逻辑回归——多分类问题
level = []
for i in range(len(scores)):
    if(scores[i] >= 85):
        level.append(2)
    elif(scores[i] >= 60):
        level.append(1)
    else:
        level.append(0)
y_train = level[:11]
y_test = level[11:]
classifier = LogisticRegression(C=1e5)
classifier.fit(X_train, y_train)
y_predict = classifier.predict(X_test)
print(y_predict)

输出：

[1 0 2]

Quiz.csv文件如下

Id	Last Score	Hours Spent	Score
1	90	117	89
2	85	109	78
3	75	113	82
4	98	20	95
5	62	116	61
6	36	34	32
7	87	120	88
8	89	132	92
9	60	83	52
10	72	92	65
11	73	112	71
12	56	143	62
13	57	97	52
14	91	119	93

 

---

• 第11章 决策树

 11.1 什么是决策树

决策树是一种非常基础又常见的机器学习模型，它是一种树型结构(可以是二叉树或非二叉树)。每个非叶节点对应一个特征，该节点的每个分支代表这个特征的一个取值，而每个叶节点存放一个类别或一个回归函数。

使用决策树进行决策的过程就是从根节点开始，提取待分类样本中相应的特征，按照其值选择输出分支，依次向下，直到到达叶子节点，将叶子节点存放的类别或者回归函数的运算结果作为输出(决策)结果。

决策树的决策过程非常直观，容易被人理解，而且运算量相对小。它在机器学习中非常重要，如果要列举“十大机器学习模型”的话，决策树应当位列前三。

决策树的作用过程很简单，那么决策树是如何构造的呢?如何通过训练来得到一棵决策树呢?

简单来讲，有以下几步。

• 准备若干训练数据(假设有m个样本)。
• 标明每个样本预期的类别。
• 选取一些特征(即决策条件)。
• 为每个训练样本所需要的特征生成相应值--数值化特征。
• 将上面(1)~(4)步获得的训练数据输入训练算法，训练算法通过一定原则决定各个特征的重要程度，然后按照决策重要性从高到低生成决策树。

那么，训练算法到底是怎样的?决定特征重要程度的原则又是什么呢?

---

11.2 几种常用算法

决策树的构造过程是一个迭代的过程。在每次次迭代中，采用不同特征作为分裂点，将样本数据划分成不同的类别。被用作分裂点的特征叫作分裂特征。

选择分裂特征的目标，是让各个分裂子集尽口能地“纯”，即尽量让一个分裂子集中的样本属于同一类别。

使各个分裂子集“纯”的算法也有多种，这里我们来看几种。

11.2.1 ID3

核心:以信息增益为度量，选择分裂后信息增益最大的特征进行分裂。

假设一个随机变量x有n种取值，分别为{v1，v2，…，vn}，每一种取值被取到的概率分别是{p1，p2，…，pn}，那么x的信息熵定义为:

信息越混乱，信息熵越大

设S为全部样本的集合，全部的样本一共分为n个类，则有

信息增益的公式为

11.2.2 C4.5

ID3有一个很大的缺点: ID3一般会优先选择应取值种类较多的特征作为分裂特征。因为取值种类多的特征会有相对较大的信息增益。

为了避免这个不足，C4.5选用信息增益率(gain ratio)(用比例而不是单纯的量)作为选择分支的标准。信息增益率通过引入一个称作分裂信息(splitinformation)的项来“惩罚”取值可能性较多的特征。

ID3 还有一个问题，就是不能处理取值在连续区间的特征。例如假设训练样本有一个特征是年龄，其取值为(0,100)的实数。ID3 就不知如何是好了。

C4.5在这方面也有弥补，具体做法如下。

1. 把需要处理的样本(对应整棵树)或样本子集(对应子树)按照连续变量的大小从小到大进行排序。
2. 假设所有m个样本数据在特征上的实际取值一共有k(k≤m)个，那么总共有k-1个可能的候选分割阈值点，每个候选的分割阈值点的值为上述排序后的特征值中两两连续元素的中点。根据这k-1个分割点把原来连续的一个特征转化为k-1个布尔特征。
3. 用信息增益率选择这k-1个特征的最佳划分。

但是，C4.5有个问题:当某个|Sv|的大小跟|S|的大小接近时:

为了避免这种情况导致某个无关紧要的特征占据根节点，可以采用启发式的思路，先计算每个特征的信息增益，在其信息增益较高的情况下，才应用信息增益率作为分裂标准。

C4.5性能优良，它对数据、运算力的要求相对较低，这使它成为机器学习最常用的算法之一。它在实际应用中的地位比 ID3 还要高。

11.2.3 CART

CART的运行过程与ID3及C4.5大致相同，不同之处在于:

1. CART的特征选取依据是Gini系数，每次选择Gini系数最小的特征作为最优切分点;
2. CART是一棵严格二叉树，每次分裂只做二分。

---

11.3 剪枝优化

• 先剪枝(局部剪枝):在构造过程中，当某个节点满足剪枝条件，直接停止此分支的构造。
• 后剪枝(全局剪枝):先构造完成完整的决策树，再通过某些条件遍历树进行剪枝。

---

11.4 代码实现

from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np

# 9 个体验差和 8 个体验好的样本数据，对应 7 个特征，Yes 取值为 1，No 为 0
features = np.array([
[1, 1, 0, 0, 1, 0, 1],
[1, 1, 1, 0, 0, 0, 1],
[0, 1, 0, 0, 0, 0, 1],
[1, 1, 0, 0, 1, 0, 1],
[0, 1, 0, 0, 1, 0, 0],
[0, 1, 0, 0, 1, 0, 1],
[1, 1, 0, 0, 1, 0, 1],
[0, 1, 0, 0, 1, 0, 1],
[0, 1, 0, 1, 1, 1, 1],
[1, 0, 1, 1, 1, 1, 0],
[0, 0, 0, 1, 1, 1, 0],
[1, 0, 1, 1, 1, 1, 0],
[0, 0, 0, 1, 1, 1, 0],
[1, 0, 0, 1, 1, 1, 0],
[0, 0, 1, 0, 1, 1, 0],
[1, 1, 1, 1, 1, 1, 0],
[1, 0, 1, 1, 1, 1, 0]
])

# 0 表示是体验“差”，1 表示是体验“好”
labels = np.array([[0], [0], [0], [0], [0], [0], [0], [0], [0], [1],
[1], [1], [1], [1], [1], [1], [1]])

# 从数据集中取 20% 作为测试集，其他作为训练集
X_train, X_test, y_train, y_test = train_test_split(
features,
labels,
test_size=0.2,
random_state=0,
)

# 训练分类树模型
clf = tree.DecisionTreeClassifier()
clf.fit(X=X_train, y=y_train)

# 测试
print(clf.predict(X_test))

# 对比测试结果和预期结果
print(clf.score(X=X_test, y=y_test))

# 预测新餐馆
new_restaurant = np.array([[1, 1, 1, 1, 1, 1, 1]])
print(clf.predict(new_restaurant))