九种机器学习模型的简单介绍
学习分类
根据数据标记分类
-
supervised learning 监督学习
- 训练集中的目标是由人标注的
-
unsupervised learning 无监督学习
- 输入数据没有被标记,也没有确定的结果。样本数据类别未知,需要根据样本间的相似性对样本集进行分类(聚类,clustering)试图使类内差距最小化,类间差距最大化。
-
SEMI-SUPERVISED learning 半监督学习
-
让学习器不依赖外界交互、自动地利用未标记样本来提升学习性能,就是半监督学习(semi-supervised learning)。
-
半监督学习可进一步划分为纯(pure)半监督学习和直推学习(transductive learning),前者假定训练数据中的未标记样本并非待测的数据,
而后者则假定学习过程中所考虑的未标记样本恰是待预测数据,学习的目的就是在这些未标记样本上获得最优泛化性能。
-
根据应用类型分类
1.REINFORCEMENT learning 强化学习
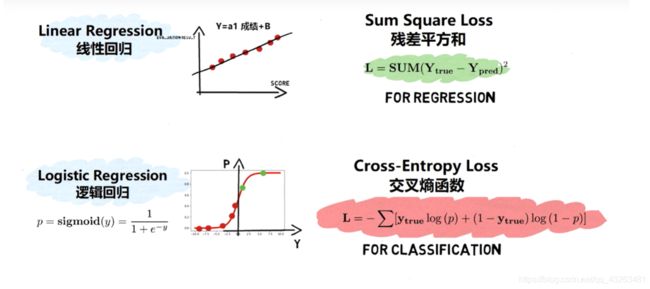
一、线性回归
二、逻辑回归
优点:计算事件概率,能减少极端值的影响
缺点:是由时间的线性分布转化为概率来进行判断,所以只适合线性分布的数据
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GyciRCqj-1597824699351)(C:\Users\Free\AppData\Roaming\Typora\typora-user-images\image-20200819104518451.png)]
实际上我们会采用更多的方法对逻辑回归的结果进行评估
如:精确度,混淆矩阵confusion matrix,f-score
三、K临近算法:环境会影响决策
K-NEAREST NEIGHBOR
step1:找到待测样本周围最近的已知样本点,这一步需要定义空间、距离公式
step2: 录入样本点信息
step3:找最近的k个样本点
step4:找到最近的k个样本点中,哪个类别最多
k临近算法和逻辑回归都是做分类问题
KNN只关注待测样本的局部分布,所以不需要用到loss函数(交叉熵函数)
逻辑回归则关注是对全局分布
KNN还可以用来做推荐系统
优点:
- 直观,好解释
- 局部分布,不需要估算整体
缺点:
- 局部估算可能不符合全局的分布
- 不能计算概率
- 对K的取值非常敏感
通常为了保证一个合理的K的取值,我们会采取交叉验证(cross-validation)找到哪个K的设置会保证最优的估算
四、决策树
决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
决策树的生成算法有ID3, C4.5和C5.0等。决策树是一种树形结构,其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果。
决策树生成的主要分为两步:
step1:节点的分裂:一般当一个节点所代表的属性无法给出判断时,则选择将这一节点分成2个
子节点(如不是二叉树的情况会分成n个子节点)
step2: 阈值的确定:选择适当的阈值使得分类错误率最小 (Training Error)。
比较常用的决策树有ID3,C4.5和CART(Classification And Regression Tree),CART的分类效果一般优于其他决策树。下面介绍具体步骤。
ID3: 由**增熵(Entropy)**原理来评估当前条件下的所有情况并决定哪个做父节点,那个节点需要分裂。
对于一组数据,熵越小说明分类结果越好。熵定义如下:
Entropy=- sum [p(x_i) * log2(P(x_i) ]
其中p(x_i) 为x_i出现的概率。假如是2分类问题,当A类和B类各占50%的时候,
Entropy = - (0.5log_2( 0.5)+0.5log_2( 0.5))= 1
当只有A类,或只有B类的时候,
Entropy= - (1*log_2( 1)+0)=0
所以当Entropy最大为1的时候,是分类效果最差的状态,当它最小为0的时候,是完全分类的状态。因为熵等于零是理想状态,一般实际情况下,熵介于0和1之间。
熵的不断最小化,实际上就是提高分类正确率的过程。
决策树是否能用来做回归问题呢?
五、梯度下降法
梯度下降(gradient descent)在机器学习中应用十分的广泛,不论是在线性回归还是Logistic回归中,它的主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。
梯度是一个向量,具有大小和方向。想象我们在爬山,从我所在的位置出发可以从很多方向上山,而最陡的那个方向就是梯度方向。
对函数 f(x1,x2,…,xn)f(x1,x2,…,xn) 来讲,对于函数上的每一个点 P(x1,x2,…,xn)P(x1,x2,…,xn),我们都可以定义一个向量 {∂f∂x1,∂f∂x2,…,∂f∂xn}{∂f∂x1,∂f∂x2,…,∂f∂xn},这个向量被称为函数 ff 在点 PP 的梯度(gradient),记为 ∇f(x1,x2,…,xn)∇f(x1,x2,…,xn) 。函数ff在PP点沿着梯度方向最陡,也就是变化速率最快。比如对于二元函数 f(x,y)f(x,y)来讲,我们先将函数的偏导数写成一个向量 {∂f∂x,∂f∂y}{∂f∂x,∂f∂y},则在点 (x0,y0)(x0,y0)处的梯度为 {∂f∂x0,∂f∂y0}{∂f∂x0,∂f∂y0}。
梯度方向是函数上升最快的方向,沿着梯度方向可以最快地找到函数的最大值,而我们要求误差的最小值,所以在梯度下降中我们要沿着梯度相反的方向。
- 梯度下降只能知道导数方向,并不知道最优点的距离,所以我们需要手动设定一个步长,他对学习率很敏感
- 不能保证全局最优性
六、Kmeans 物以类聚
是无监督学习
- 随机从数据集中选取K个样本当做centroids
- 对于数据集中的每个点,计算它距离每个centroid的距离,并把它归为距离最近的那个cluster
- 更新新的centroid位置
- 重复2.3,知道centroid的位置不再改变
优点:非监督类的算法不需要样本的标注信息
缺点:
-
不能利用到数据的标注信息,意味着模型的性能不如其他监督学习
-
对于K的取值,也就是你认为数据集中的样本应该分为几类,这个参数的设置极为敏感
七、向量支持机
目的是找到分界面,并最大化这个间距
即等于最小化间距倒数的平方
SVMLOSS FUNCTION: Loss(β)= ||β||^2/2
所以也叫大间隔分类器
优点:
- 是强分类器,能保证最大化区分两个类别,所以模型的性能优异
缺点:
-
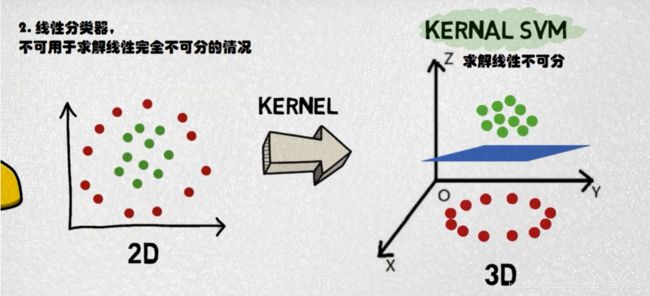
Hard-margin SVM是线性分类器不能处理不同类别相互交融情况
-
在这种情况下可以强制允许对于一些错误样本的分类来保持大体上的容错率
这就是 SOFT_MARGINSVM
-
分类器,不可用于求解线性完全不可分的情况 当出现这种情况时,会引入KERNEL,来把数据映射到更高的维度,用线性超平面去使用。
八、随机森林
是一种集成学习中Bagging类型算法(Bootstrap Aggregation
)即引导聚合类算法,内部是多个弱监督模型结合,这类算法不专注于解决困难样本,所以模型的Performance往往会受限,集成学习中的另一种算法Boosting,即可解决这种缺点。
森林意思是模型中包含很多决策树
随机意思是从数据集中采用以训练模型中的每颗决策树(即看问题角度不一样)
设计步骤:
-
预设模型的超参数,几棵树,分几层?
-
随机采用,训练每个决策树
-
输入待测样本到每个树中,再将每个树的结果整合
求均值或者求众数
优点:
- 模型随机性很强,不容易overfit,但是抗噪性强,表示对异常点outlier不敏感
- 处理高位数据相对更快
- 树状结构,模型可解释度高,可以告诉你每个特征的重要性
缺点:
模型往往过于General不具备正确处理过于困难的样本的能力
九、Adaboost
可以解决随机森林的问题,一句话总结特点,前人栽树,后人乘凉!
ADABOOST:自适应增强算法
后一个模型的训练永远是在前一个模型的基础上完成的,是顺序,级联的结构
step1:对于训练每个weak learner计算样本困难度
- 初始化所有样本的困难度为 wi= 1/N
- 利用当前weak learner的训练结果 更新所有样本的困难度,如果正确则减少困难反正增加
- 然后在这个基础上训练下一个模型
step2:学习每个weak learner的权重
然后权限*输出整合起来
优点
- 顺序,级联的结构+利用权重组合结果擅长解决困难问题
- 模型性能的天花板高
缺点:
- 容易Overfit
- 对于异常点Outlier过于敏感,模型的性能起点低
- 速度慢