深度学习入门（三十三）卷积神经网络——ResNet

前言

核心内容来自博客链接1博客连接2希望大家多多支持作者
本文记录用，防止遗忘

卷积神经网络——ResNet

课件

加更多的层总是改进精度吗？

残差块

1、串联一个层改变函数类，我们希望能扩大函数类
2、残差块加入快速通道(右边）来得到f(x)=x＋g(x)的结构

ResNet块细节

不同的残差块

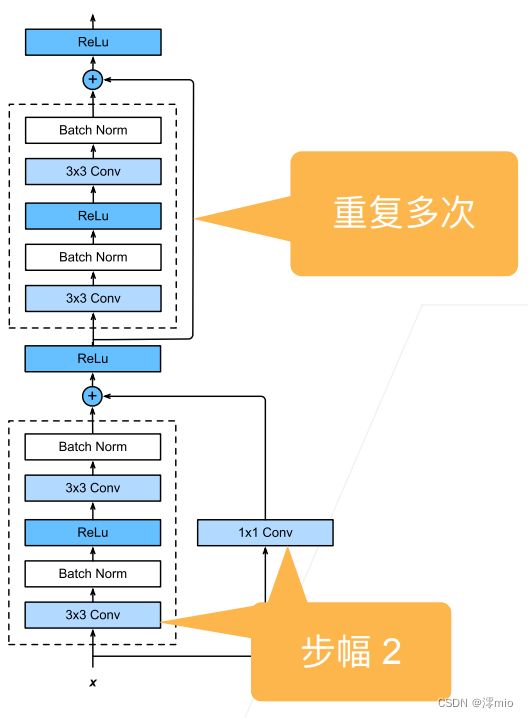
ResNet块

1、高宽减半ResNet块(步幅2)
2、后接多个高宽不变ResNet块

ResNet架构

类似VGG和GoogleNet的总体架构，但替换成了ResNet块

总结

1、残差块使得很深的网络更加容易训练，甚至可以训练一千层的网络
2、残差网络对随后的深层神经网络设计产生了深远影响，无论是卷积类网络还是全连接类网络。

教材

随着我们设计越来越深的网络，深刻理解“新添加的层如何提升神经网络的性能”变得至关重要。更重要的是设计网络的能力，在这种网络中，添加层会使网络更具表现力， 为了取得质的突破，我们需要一些数学基础知识。

1 函数类

首先，假设有一类特定的神经网络架构$\mathcal{F}$，它包括学习速率和其他超参数设置。 对于所有$f\in \mathcal{F}$，存在一些参数集（例如权重和偏置），这些参数可以通过在合适的数据集上进行训练而获得。 现在假设$f^{\ast }$是我们真正想要找到的函数，如果是$f^{\ast }\in \mathcal{F}$，那我们可以轻而易举的训练得到它，但通常我们不会那么幸运。 相反，我们将尝试找到一个函数$f_{\mathcal{F}}^{\ast }$，这是我们在中的最佳选择。 例如，给定一个具有特性和标签的数据集，我们可以尝试通过解决以下优化问题来找到它：
$$f_{\mathcal{F}}^{\ast }:={\mathrm{argmin}}_{f}L(\mathbf{X},\mathbf{y},f)\text{ subject to }f\in \mathcal{F}.$$

2 残差块

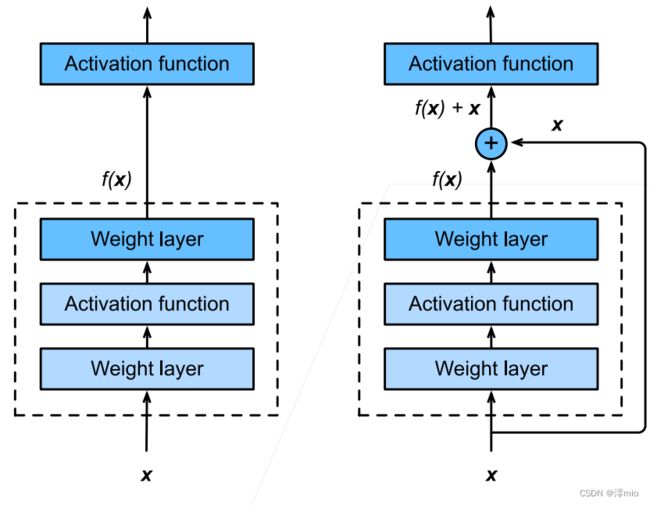
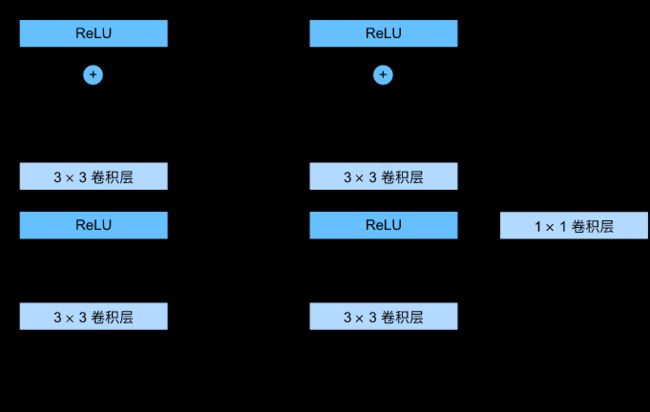
让我们聚焦于神经网络局部：如图所示，假设我们的原始输入为$x$，而希望学出的理想映射为$f(\mathbf{x})$（作为图上方激活函数的输入）。 左图虚线框中的部分需要直接拟合出该映射，而右图虚线框中的部分则需要拟合出残差映射。 残差映射在现实中往往更容易优化。 以本节开头提到的恒等映射作为我们希望学出的理想映射，我们只需将右图虚线框内上方的加权运算（如仿射）的权重和偏置参数设成0，那么即为恒等映射。 实际中，当理想映射极接近于恒等映射时，残差映射也易于捕捉恒等映射的细微波动。 右图是ResNet的基础架构–残差块（residual block）。 在残差块中，输入可通过跨层数据线路更快地向前传播。

ResNet沿用了VGG完整的$3\times 3$卷积层设计。 残差块里首先有2个有相同输出通道数的$3\times 3$卷积层。 每个卷积层后接一个批量规范化层和ReLU激活函数。 然后我们通过跨层数据通路，跳过这2个卷积运算，将输入直接加在最后的ReLU激活函数前。 这样的设计要求2个卷积层的输出与输入形状一样，从而使它们可以相加。 如果想改变通道数，就需要引入一个额外的$1\times 1$卷积层来将输入变换成需要的形状后再做相加运算。 残差块的实现如下：

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Residual(nn.Module):  #@save
    def __init__(self, input_channels, num_channels,
                 use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)

如图所示，此代码生成两种类型的网络： 一种是当use_1x1conv=False时，应用ReLU非线性函数之前，将输入添加到输出。 另一种是当use_1x1conv=True时，添加通过卷积调整通道和分辨率。

下面我们来查看输入和输出形状一致的情况。

blk = Residual(3,3)
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
Y.shape

输出：

torch.Size([4, 3, 6, 6])

我们也可以在增加输出通道数的同时，减半输出的高和宽。

blk = Residual(3,6, use_1x1conv=True, strides=2)
blk(X).shape

输出：

torch.Size([4, 6, 3, 3])

3 ResNet模型

ResNet的前两层跟之前介绍的GoogLeNet中的一样： 在输出通道数为64、步幅为2的$7\times 7$卷积层后，接步幅为2的$3\times 3$最大汇聚层。 不同之处在于ResNet每个卷积层后增加了批量规范化层。

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

GoogLeNet在后面接了4个由Inception块组成的模块。 ResNet则使用4个由残差块组成的模块，每个模块使用若干个同样输出通道数的残差块。 第一个模块的通道数同输入通道数一致。 由于之前已经使用了步幅为2的最大汇聚层，所以无须减小高和宽。 之后的每个模块在第一个残差块里将上一个模块的通道数翻倍，并将高和宽减半。

下面我们来实现这个模块。注意，我们对第一个模块做了特别处理。

def resnet_block(input_channels, num_channels, num_residuals,
                 first_block=False):
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            blk.append(Residual(input_channels, num_channels,
                                use_1x1conv=True, strides=2))
        else:
            blk.append(Residual(num_channels, num_channels))
    return blk

接着在ResNet加入所有残差块，这里每个模块使用2个残差块。

b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

最后，与GoogLeNet一样，在ResNet中加入全局平均汇聚层，以及全连接层输出。

net = nn.Sequential(b1, b2, b3, b4, b5,
                    nn.AdaptiveAvgPool2d((1,1)),
                    nn.Flatten(), nn.Linear(512, 10))

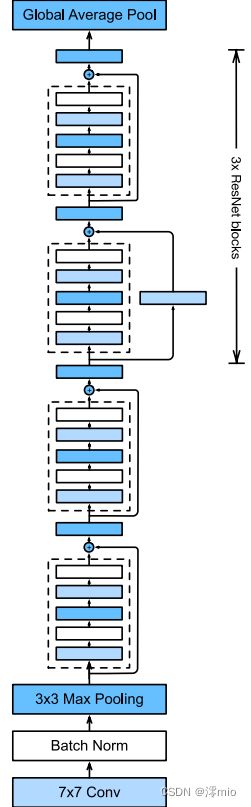
每个模块有4个卷积层（不包括恒等映射的$1\times 1$卷积层）。 加上第一个$7\times 7$卷积层和最后一个全连接层，共有18层。 因此，这种模型通常被称为ResNet-18。 通过配置不同的通道数和模块里的残差块数可以得到不同的ResNet模型，例如更深的含152层的ResNet-152。 虽然ResNet的主体架构跟GoogLeNet类似，但ResNet架构更简单，修改也更方便。这些因素都导致了ResNet迅速被广泛使用。 下图描述了完整的ResNet-18。

在训练ResNet之前，让我们观察一下ResNet中不同模块的输入形状是如何变化的。 在之前所有架构中，分辨率降低，通道数量增加，直到全局平均汇聚层聚集所有特征。

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

输出;

Sequential output shape:     torch.Size([1, 64, 56, 56])
Sequential output shape:     torch.Size([1, 64, 56, 56])
Sequential output shape:     torch.Size([1, 128, 28, 28])
Sequential output shape:     torch.Size([1, 256, 14, 14])
Sequential output shape:     torch.Size([1, 512, 7, 7])
AdaptiveAvgPool2d output shape:      torch.Size([1, 512, 1, 1])
Flatten output shape:        torch.Size([1, 512])
Linear output shape:         torch.Size([1, 10])

4 训练模型

同之前一样，我们在Fashion-MNIST数据集上训练ResNet。

lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

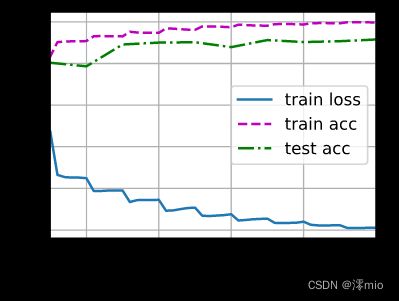
输出：

loss 0.011, train acc 0.997, test acc 0.915
4701.1 examples/sec on cuda:0

5 小结

1、学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。
2、残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。
3、利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。
4、残差网络（ResNet）对随后的深层神经网络设计产生了深远影响。

参考文献

[1] He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).

[2] He, K., Zhang, X., Ren, S., & Sun, J. (2016, October). Identity mappings in deep residual networks. In European Conference on Computer Vision (pp. 630-645). Springer, Cham.