论文阅读 MAML (Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks)
Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks MAML 论文阅读
- 摘要
- 介绍
- 模型不可知元学习
-
- 元学习问题定义
- 模型不可知元学习算法
- MAML种类
-
- 监督回归和分类
- 强化学习
- 总结
Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
用于深度网络快速自适应的模型不可知元学习
摘要
元学习的目标是在各种学习任务上训练一个模型,学习一个模型初始化,这样它可以只使用少量的训练样本来解决新的学习任务。也就是说训练一个具体对各种任务都有极强泛化性的模型,在新任务中只需要小样本训练对参数进行微调即可。文章中,该方法可以用到分类、回归和强化学习的方法中。
介绍
快速学习要求对大量任务训练学习先验知识,再将其与新任务的数据相结合,并防止在新任务中过拟合。
在元学习中,目标是从少量新数据中快速学习新任务,元学习器训练模型以学习大量不同的任务。其关键思想是训练模型的初始参数,以便在通过一个或多个梯度步长更新参数后,模型在新任务上具有最大性能,该梯度步长是用来自该新任务的少量数据计算的。
元学习的新任务快速学习可以视为构建广泛适用于许多任务的内部表示。如果内部表示适用于许多任务,那么简单地稍微微调参数可以产生良好的结果。
并且元学习与模型的类型无关。
模型不可知元学习
元学习的目标是训练能够实现快速适应的模型,这一问题设置通常被正式化为少量学习。
元学习问题定义
元学习的目标是训练一个模型,该模型仅使用几个数据点和训练迭代就能快速适应新任务。方法是在元学习阶段对模型或学习者进行一组任务的训练。
一个任务的定义形式如下:
L为损失函数, q ( x 1 ) q(x1) q(x1)为初始观测的概率, q ( x t + 1 ∣ x t , a t ) q(x_{t+1}|x_{t}, a_{t}) q(xt+1∣xt,at)为状态转移概率,H为一个episode的长度。(任务定义更针对强化学习)对分类和回归任务H一般为1。
![]()
模型不可知元学习算法
先前的工作试图训练摄取整个数据集的递归神经网络或可在测试时与非参数方法结合的特征嵌入。
元学习思想是,一些内部表征比其他表征更容易传递。例如,神经网络可能学习广泛适用于p(T)中所有任务的内部特征,而不是单个任务。我们如何鼓励这种通用表示的出现?我们的目标是找到对任务变化敏感的模型参数,这样,当沿着损失梯度的方向改变时,参数的微小变化将对从p(T)得出的任何任务的损失函数产生很大的改善。
元学习的算法流程如下:

其中2-8为外部循环,4-7为内部循环。
2:开始循环
3:首先这里会采样多个任务
4:对于各个任务进行内部循环
5:对于各个任务中采样得到的K个样本(训练集)根据损失计算参数 θ \theta θ梯度
6:使用梯度下降计算当前的自适应参数 θ ′ \theta^{'} θ′,计算公式为:
![]()
注意我们这里并没有直接使用 θ ′ \theta^{'} θ′来替换 θ \theta θ,而仅仅是计算了 θ ′ \theta^{'} θ′的值,这是为了进一步计算下一步更新的梯度。
7: 结束内循环
8:外循环最重要的一步,更新任务的参数目标 θ \theta θ,更新公式为

注意这里是使用每个任务的测试集来更新。同时注意求导过程中,这里是使用的各个任务中基于 θ ′ \theta^{'} θ′的模型对于初始参数 θ \theta θ的梯度的和。

补充:注意这个求导公式涉及到了 θ \theta θ的二阶导。如下图,由于首先需要对 θ ′ \theta^{'} θ′进行求导,进一步对 θ ′ \theta^{'} θ′求 θ \theta θ的倒数,推导如下:

但是在实现过程中MAML对这个二阶导的计算做了近似,因为不近似的话二阶导要保存计算图,存储空降和计算速度都会受到影响,会花费大量的计算时间。这里近似把二阶导数置为0。
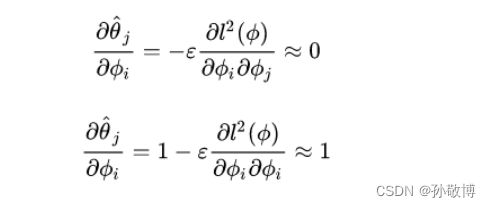
因此在实际代码中 f ( θ ′ ) f(\theta^{'}) f(θ′)对 θ \theta θ求导等价于 f ( θ ′ ) f(\theta^{'}) f(θ′)对 θ ′ \theta^{'} θ′求导。如下是计算时的关键代码。
for i in range(task_num):
# 1. run the i-th task and compute loss for k=0
logits = self.net(x_spt[i], vars=None, bn_training=True)
loss = F.cross_entropy(logits, y_spt[i])
#可以看到下面的这个grad的计算图没有保存
grad = torch.autograd.grad(loss, self.net.parameters())
fast_weights = list(map(lambda p: p[1] - self.update_lr * p[0], zip(grad, self.net.parameters())))
for k in range(1, self.update_step): #第二步更新了
logits = self.net(x_spt[i], fast_weights, bn_training=True)
loss = F.cross_entropy(logits, y_spt[i])
grad = torch.autograd.grad(loss, fast_weights)
#这里就不用对net的参数求导,近似为对fastw求导
fast_weights = list(map(lambda p: p[1] - self.update_lr * p[0], zip(grad, fast_weights)))
logits_q = self.net(x_qry[i], fast_weights, bn_training=True)
# loss_q will be overwritten and just keep the loss_q on last update step.
loss_q = F.cross_entropy(logits_q, y_qry[i])
losses_q[k + 1] += loss_q
self.meta_optim.zero_grad()
loss_q.backward()
self.meta_optim.step()
#这里的loss是对net的参数求导,虽然里面有fastw,但由于没有保存计算图,所以其对net的导数为1
代码来自:https://blog.csdn.net/Cecilia6277/article/details/109091482
MAML种类
监督回归和分类
强化学习
总结
因此,个人认为元学习这篇文章主要的几点如下:
- 首先,元学习是用来解决小样本快速学习的。他的方法是在多种任务上进行训练的基础上,学习到泛化的共同信息,生成初始化网络的参数。在新任务上使用这种初始化网络参数可以快速收敛。
- 其次,元学习的具体实现如下:
(1) 首先对迭代次数进行循环,进入外循环,外循环中会采集任务样本。
(2) 之后进入内循环,内循环会对所有的任务进行循环,第一步使用训练任务的训练进行训练,预估损失对于参数的梯度,并使用梯度更新一次参数,得到初始化模型参数 θ ′ \theta^{'} θ′,内循环结束。
(3) 然后退出到外循环,使用各个任务的测试集和初始化模型参数 θ ′ \theta^{'} θ′对于 θ \theta θ的梯度的和来更新 θ \theta θ,获得初始化参数。

- 实现补充
在进行上面外循环的最后一步更新时,对于初始化模型 f ( θ ′ ) f(\theta^{'}) f(θ′)对于 θ \theta θ的梯度涉及到对于 θ \theta θ的二阶导数,计算时会花费大量的时间,因此为更好地计算,将二阶导数近似为0,因此近似为初始化模型 f ( θ ′ ) f(\theta^{'}) f(θ′)对于 θ ′ \theta^{'} θ′的梯度。 - 更新示意图
因此最终的更新方式如下图,理论上使用第二次在 θ m \theta^{m} θm基础上对原始 ϕ 0 \phi^{0} ϕ0的梯度来更新 ϕ 0 \phi^{0} ϕ0。近似后变为第二次在 θ m \theta^{m} θm基础上对 θ m \theta^{m} θm的梯度来更新 ϕ 0 \phi^{0} ϕ0。

- 强化学习目标
希望初始化一组参数 θ \theta θ,使得训练过一次后的模型能够得到最大奖励。因此可能这也是元学习中如此设计更新步骤的原因。



