Chapter2 机器学习回顾与Pytorch的基本操作

目录

2.1 机器学习的本质是分类与回归

2.1.1 分类问题

2.1.2 回归问题

2.1.3 构成机器学习的元素

2.2 Pytorch的基本概念

2.2.1 张量、变量与nn.module

2.2.2 张量与机器学习的关系

2.3 tensor编程基础

2.3.1 正常定义的tensor(ones、eye、zeros)

2.3.2 特殊定义的tensor (zeros_like、ones_like)

2.3.3  特殊定义的tensor (rand（随机）、normal（正态分布）、uniform（均匀分布）、arange（序列）、linspace（等间隔）)

2.3.4 tensor的属性

2.3.5 tensor的算术无运算编程（一）

 2.3.6 Pytorch中的inplace操作与广播机制

2.3.7 Tensor的取整、取余操作

2.3.8 Tensor的比较运算

2.3.9 Tensor的三角函数

2.3.10 Tensor中其他的数学函数

---

2.1 机器学习的本质是分类与回归

2.1.1 分类问题

        分类问题：

         如上图所示是一个分类问题，即给你一张图片让你输出它的类别，对于类别的值我们采用离散的值来描述，我们最终输出的是一个十维的概率分布，概率值指向最大的维度就是我们最终的分类结果。

2.1.2 回归问题

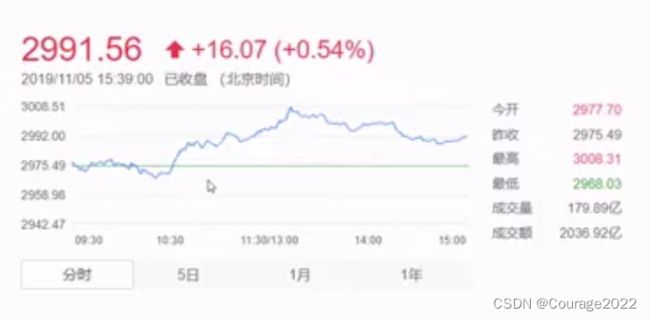
        回归问题：

         如上图是一个股票价格波动的一个曲线，回归值解决的就是连续值的预测，如果我们机器学习最终的预测模型是一个连续模型，我们将它定义为回归问题。如股票价格的预测、身高的预测、房价的预测等等。

2.1.3 构成机器学习的元素

        样本、模型、训练、测试、推理。

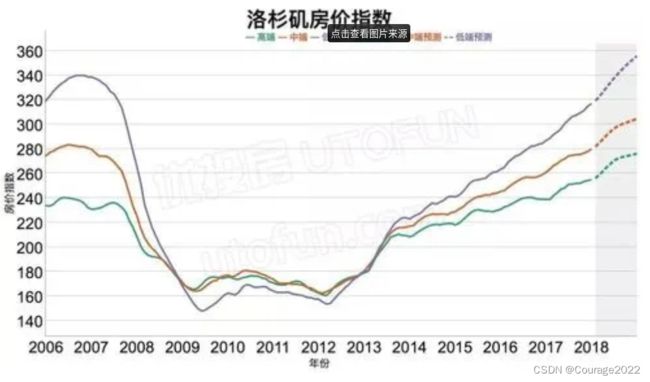
        拿房价预测做举例：

        样本：样本由属性与标签构成，可以理解为函数形式，对应属性，对应标签。在上图房价预测这个问题中，属性指年份、标签指房价指数。

        模型：为了拟合这个属性相对于标签的函数，我们假定拟合模型为。当然这可能不是最好的，只是一个假定而已。

        训练：在我们本科阶段，解方程是几个未知数对应几元方程，但在机器学习中不同，我们拿（属性，标签）的海量数据对模型参数进行训练，也就是说（参数数量远小于样本量），最终我们通过本专栏内容训练出了模型参数。（深度学习的模型参数数量远大于样本量）

        测试：我们拿代价函数评判这个函数的好坏。

        推理：对于一个新的没有标签的属性数据，我们要推理它的属性。比如我们通过所给模型来预测2090年的房价指数。

2.2 Pytorch的基本概念

2.2.1 张量、变量与nn.module

Tensor：张量

        我们之前描述物体所用的形式：标量、向量、矩阵只能描述1维、n维、维的事物，而用这些描述形式最多可以描述维的事物无法描述高维，而我们用张量可以描述任意维度的事物。可以理解向量是1维张量、矩阵是2维张量。拿房价预测来讲，房价可能受地域、面积、海拔等不同因素影响，用低维张量难以表示。

Variable：变量

         机器学习人物中用变量表达参数。

nn.module：解决计算机视觉问题所用的网络结构

2.2.2 张量与机器学习的关系

        机器学习就是用tensor表达样本，一条语音数据用一个向量进行描述（采样后的波形）、图像灰度图用二阶张量来描述（0-256 h*w矩阵）。

2.3 tensor编程基础

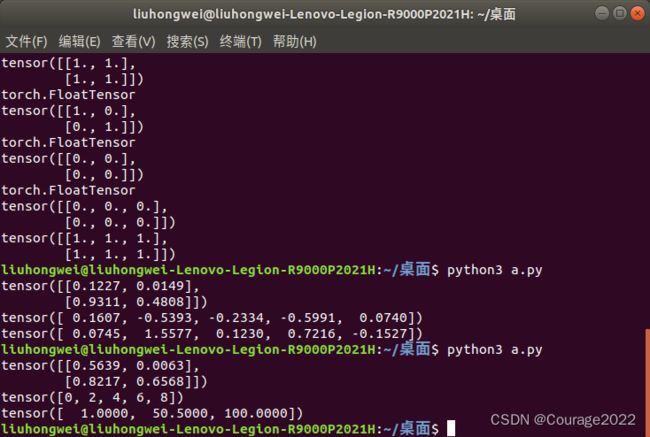
2.3.1 正常定义的tensor(ones、eye、zeros)

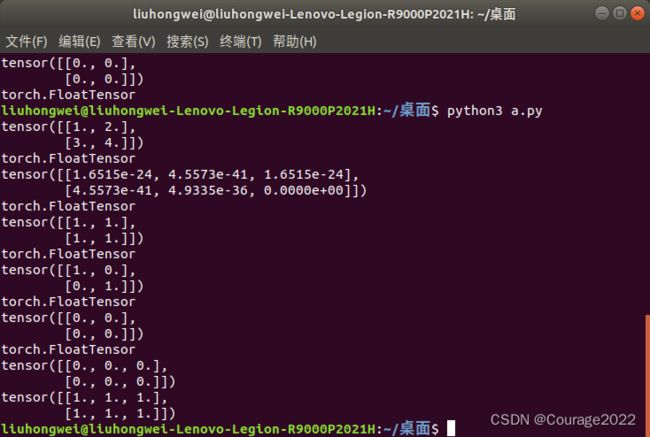
import torch

a = torch.Tensor([[1,2],[3,4]])

print(a)
print(a.type())

b = torch.Tensor(2,3)
print(b)
print(b.type())

c = torch.ones(2,2)
print(c)
print(c.type())

d = torch.eye(2,2)
print(d)
print(d.type())

e = torch.zeros(2,2)
print(e)
print(e.type())

         可以看出不加声明的话tensor中的元素都是float类型的，如果仅仅对tensor进行声明输出的是内存数据。eye对应单位矩阵，zeros对应零矩阵。

2.3.2 特殊定义的tensor (zeros_like、ones_like)

import torch

a = torch.Tensor([[1,2],[3,4]])

print(a)
print(a.type())

b = torch.Tensor(2,3)
print(b)
print(b.type())

c = torch.ones(2,2)
print(c)
print(c.type())

d = torch.eye(2,2)
print(d)
print(d.type())

e = torch.zeros(2,2)
print(e)
print(e.type())

f = torch.zeros_like(b)
g = torch.ones_like(b)
print(f)
print(g)

         可以看出，用此种方法定义出的tensor保留了原来的格式并赋予了新的赋值方法。

2.3.3  特殊定义的tensor (rand（随机）、normal（正态分布）、uniform（均匀分布）、arange（序列）、linspace（等间隔）)

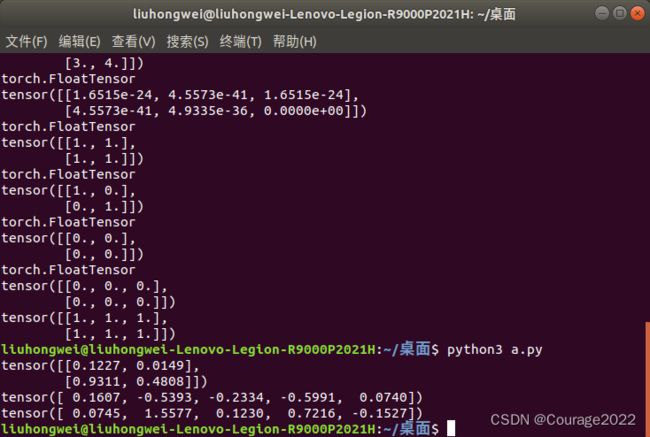
import torch

a = torch.rand(2,2)
print(a)

a = torch.normal(mean = 0.0,std = torch.rand(5))
print(a)

a = torch.normal(mean = torch.rand(5),std = torch.rand(5))
print(a)

        生成随机值与生成正态分布值。

        生成正态分布值解释：我们初始化均值mean、方差std为五组不同的数据，即五组不同的正态分布，我们再从这五组不同的正态分布随机生成满足正态分布的五个值。

import torch

a = torch.Tensor(2,2).uniform_(-1,1)
print(a)

a = torch.arange(0,10,2)
print(a)

a = torch.linspace(1,100,3)
print(a)

         都很好理解，不加解释。

2.3.4 tensor的属性

        每一个tensor有torch.dtype、torch.device、torch.layout三种属性

        torch.dtype标识了数据类型。

        torch.device标识了tensor.Tensor对象在创建之后所存储在的设备名称（CPU、GPU）。

        torch.layout表示tensor.Tensor内存布局的对象（稠密，稀疏）。

        定义稠密张量无须多言是一种缺创建省的方式：

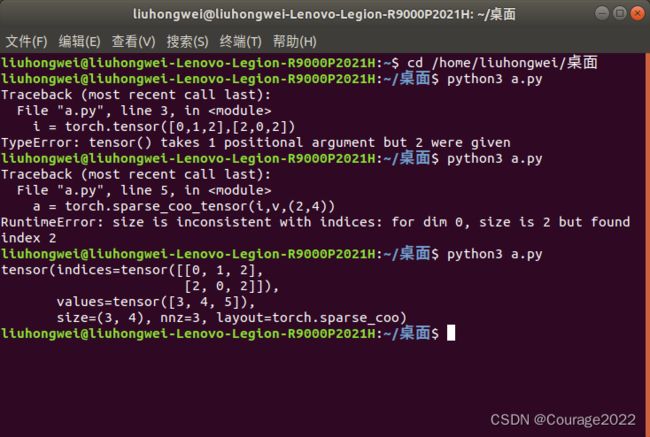
torch.tensor([1,2,3],dtype=torch.float32,device=torch.device('cpu'))

        定义稀疏张量：torch.sparse_coo_tensor，coo类型表示了非零元素的坐标形式：

        类似于数据结构的稀疏矩阵可以大量节省内存，如下代码的含义是三组坐标的值非零，值为，类型为float32，是一个的tensor。

import torch

i = torch.tensor([[0,1,2],[2,0,2]])
v = torch.tensor([3,4,5])
a = torch.sparse_coo_tensor(i,v,(3,4))

print(a)

        稀疏张量转换成稠密张量：

a = torch.sparse_coo_tensor(i,v,(3,4)).to_dense()

 

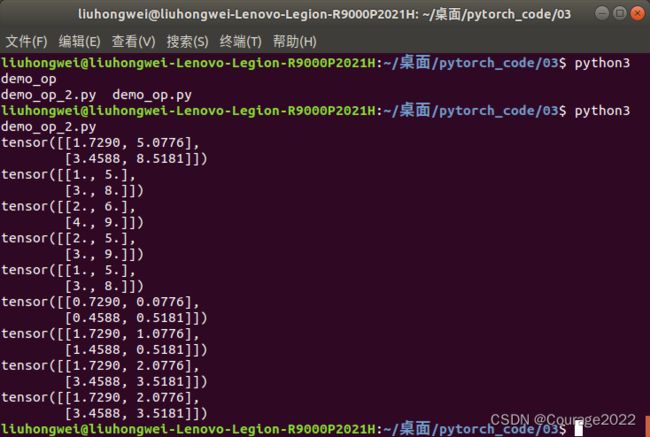
2.3.5 tensor的算术无运算编程（一）

无

liuhongwei@liuhongwei-Lenovo-Legion-R9000P2021H:~/桌面/pytorch_code/03$ python3 demo_op.py 
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.3559, 0.5683, 0.2320],
        [0.1876, 0.4727, 0.2266]])
tensor([[0.9451, 0.7173, 0.4475],
        [0.3638, 0.7806, 0.3054]])
tensor([[0.9451, 0.7173, 0.4475],
        [0.3638, 0.7806, 0.3054]])
tensor([[0.9451, 0.7173, 0.4475],
        [0.3638, 0.7806, 0.3054]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.9451, 0.7173, 0.4475],
        [0.3638, 0.7806, 0.3054]])
tensor([[0.9451, 0.7173, 0.4475],
        [0.3638, 0.7806, 0.3054]])
==== sub res ====
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
===== mul ====
tensor([[0.2097, 0.0847, 0.0500],
        [0.0331, 0.1455, 0.0179]])
tensor([[0.2097, 0.0847, 0.0500],
        [0.0331, 0.1455, 0.0179]])
tensor([[0.2097, 0.0847, 0.0500],
        [0.0331, 0.1455, 0.0179]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.2097, 0.0847, 0.0500],
        [0.0331, 0.1455, 0.0179]])
tensor([[0.2097, 0.0847, 0.0500],
        [0.0331, 0.1455, 0.0179]])
=== div ===
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[0.5891, 0.1490, 0.2156],
        [0.1762, 0.3079, 0.0788]])
tensor([[1., 1.],
        [1., 1.]])
tensor([[1., 1.],
        [1., 1.]])
tensor([[1., 1.],
        [1., 1.]])
tensor([[1., 1.],
        [1., 1.]])
tensor([[1., 1.],
        [1., 1.]])
torch.Size([1, 2, 3, 3])
tensor([1, 8])
tensor([1, 8])
tensor([1, 8])
tensor([1, 8])
tensor([1, 8])
torch.FloatTensor
tensor([2.7183, 7.3891])
tensor([2.7183, 7.3891])
tensor([  15.1543, 1618.1781])
tensor([  15.1543, 1618.1781])
tensor([2.3026, 0.6931])
tensor([2.3026, 0.6931])
tensor([ 0.8340, -0.3665])
tensor([ 0.8340, -0.3665])
tensor([3.1623, 1.4142])
tensor([3.1623, 1.4142])
tensor([1.7783, 1.1892])
tensor([1.7783, 1.1892])

 2.3.6 Pytorch中的inplace操作与广播机制

        inplace操作即不允许使用临时变量。也称为原地操作。x = x+y。比如add_、sub_、mul_

        广播机制即张量参数可以自动扩展为相同大小，广播机制要满足两个条件：

        1.每个张量至少有一个维度  2.满足右对齐

torch.rand(2,1,1)+torch.rand(3)

        所谓右对齐，以这两个张量以右边进行对齐。也即"3与1进行对齐"，3前面没有维度我们进行补1，也即这个维度，我们从右向左看，满足两个条件（要么相等，要么一个为1）我们认为是右对齐的。（实例中有个1我们认为满足右对齐）

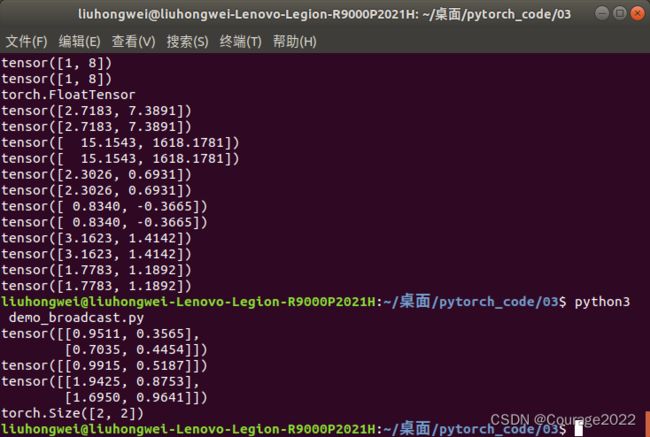
import torch

a = torch.rand(2, 2)
b = torch.rand(1, 2)
# a, 2*1
# b, 1*2
# c, 2*2
# 2*4*2*3
c = a + b
print(a)
print(b)
print(c)
print(c.shape)

        我们看到，将第一行进行相加，再把第一行拷贝到第二行进行相加得到结果。

        我们来看一个复杂的例子：

import torch

a = torch.rand(2,1,1,3)
b = torch.rand(4,2,3)

c = a + b
print(a)
print(b)
print(c)
print(c.shape)

        我们可以预测到我们输出的向量维为，我们看看结果。

liuhongwei@liuhongwei-Lenovo-Legion-R9000P2021H:~/桌面/pytorch_code/03$ python3  demo_broadcast.py 
tensor([[[[0.3442, 0.7778, 0.3574]]],


        [[[0.0979, 0.8217, 0.0140]]]])
tensor([[[0.4133, 0.1959, 0.4576],
         [0.4061, 0.8951, 0.3582]],

        [[0.7706, 0.4344, 0.5427],
         [0.5669, 0.4276, 0.7704]],

        [[0.6270, 0.5850, 0.8272],
         [0.7869, 0.1770, 0.5247]],

        [[0.3716, 0.6591, 0.5735],
         [0.9159, 0.4745, 0.2106]]])
tensor([[[[0.7575, 0.9737, 0.8149],
          [0.7503, 1.6729, 0.7155]],

         [[1.1148, 1.2122, 0.9000],
          [0.9111, 1.2054, 1.1277]],

         [[0.9712, 1.3629, 1.1846],
          [1.1311, 0.9549, 0.8820]],

         [[0.7158, 1.4370, 0.9309],
          [1.2601, 1.2524, 0.5680]]],


        [[[0.5112, 1.0176, 0.4716],
          [0.5040, 1.7168, 0.3722]],

         [[0.8685, 1.2561, 0.5567],
          [0.6648, 1.2494, 0.7844]],

         [[0.7249, 1.4068, 0.8412],
          [0.8848, 0.9988, 0.5387]],

         [[0.4695, 1.4809, 0.5875],
          [1.0138, 1.2963, 0.2246]]]])
torch.Size([2, 4, 2, 3])

2.3.7 Tensor的取整、取余操作

我们具体看看代码操作：

import torch

a = torch.rand(2, 2)
a = a * 10
print(a)

print(torch.floor(a))
print(torch.ceil(a))
print(torch.round(a))
print(torch.trunc(a))
print(torch.frac(a))
print(a % 2)
b = torch.tensor([[2, 3], [4, 5]],
                 dtype=torch.float)
print(torch.fmod(a, b))
print(torch.remainder(a, b))

2.3.8 Tensor的比较运算

 

import torch

a = torch.rand(2, 3)
b = torch.rand(2, 3)

print(a)
print(b)

print(torch.eq(a, b))             #判断每一个元素是否相等 返回一个2*3张量 元素为true、false
print(torch.equal(a, b))          #如果全相等（shape和元素值）返回true

print(torch.ge(a, b))
print(torch.gt(a, b))
print(torch.le(a, b))
print(torch.lt(a, b))
print(torch.ne(a, b))

####

a = torch.tensor([[1, 4, 4, 3, 5],
                  [2, 3, 1, 3, 5]])
print(a.shape)                                    #2*5
print(torch.sort(a, dim=1,
                 descending=False))
#输出如下： 
#torch.Size([2, 5])
#values=tensor([[1, 3, 4, 4, 5],
#        [1, 2, 3, 3, 5]]),
#indices=tensor([[0, 3, 1, 2, 4],
#        [2, 0, 1, 3, 4]]))   在原来的tensor中的索引值
#dim是指定轴的意思：如果dim=0则会对1，2   4，3  4，1 3，3 5，5排序  dim=1会对两个序列进行排序


##topk
a = torch.tensor([[2, 4, 3, 1, 5],
                  [2, 3, 5, 1, 4]])
print(a.shape)                                        #2*5

print(torch.topk(a, k=2, dim=1, largest=False))       #dim=0 指向2的维度  dim=1 指向5的维度 

print(torch.kthvalue(a, k=2, dim=0))       #第0维（2）第二小的数
#values=tensor([2, 4, 5, 1, 5]),
#indices=tensor([1, 0, 1, 1, 0]))


print(torch.kthvalue(a, k=2, dim=1))       #第1维（5）第二个最小值
#values=tensor([2, 2]),
#indices=tensor([0, 0]))

a = torch.rand(2, 3)
print(a)
print(a/0)
print(torch.isfinite(a))    ##有界
print(torch.isfinite(a/0))  ##有界
print(torch.isinf(a/0))     ##无界
print(torch.isnan(a))       ##nan

import numpy as np
a = torch.tensor([1, 2, np.nan])
print(torch.isnan(a))

a = torch.rand(2, 3)
print(a)
print(torch.topk(a, k=2, dim=1, largest=False))
print(torch.topk(a, k=2, dim=1, largest=True))

liuhongwei@liuhongwei-Lenovo-Legion-R9000P2021H:~/桌面/pytorch_code/03$ python3 demo_compare.py 
tensor([[0.0923, 0.9738, 0.9263],
        [0.8390, 0.9426, 0.7391]])
tensor([[0.1983, 0.1863, 0.0867],
        [0.7300, 0.9369, 0.6763]])
tensor([[False, False, False],
        [False, False, False]])
False
tensor([[False,  True,  True],
        [ True,  True,  True]])
tensor([[False,  True,  True],
        [ True,  True,  True]])
tensor([[ True, False, False],
        [False, False, False]])
tensor([[ True, False, False],
        [False, False, False]])
tensor([[True, True, True],
        [True, True, True]])
torch.Size([2, 5])
torch.return_types.sort(
values=tensor([[1, 3, 4, 4, 5],
        [1, 2, 3, 3, 5]]),
indices=tensor([[0, 3, 1, 2, 4],
        [2, 0, 1, 3, 4]]))
torch.Size([2, 5])
torch.return_types.topk(
values=tensor([[1, 2],
        [1, 2]]),
indices=tensor([[3, 0],
        [3, 0]]))
torch.return_types.kthvalue(
values=tensor([2, 4, 5, 1, 5]),
indices=tensor([1, 0, 1, 1, 0]))
torch.return_types.kthvalue(
values=tensor([2, 2]),
indices=tensor([0, 0]))
tensor([[0.4250, 0.6952, 0.5542],
        [0.5016, 0.5173, 0.9565]])
tensor([[inf, inf, inf],
        [inf, inf, inf]])
tensor([[True, True, True],
        [True, True, True]])
tensor([[False, False, False],
        [False, False, False]])
tensor([[True, True, True],
        [True, True, True]])
tensor([[False, False, False],
        [False, False, False]])
tensor([False, False,  True])
tensor([[0.7347, 0.2777, 0.1669],
        [0.7062, 0.7895, 0.7085]])
torch.return_types.topk(
values=tensor([[0.1669, 0.2777],
        [0.7062, 0.7085]]),
indices=tensor([[2, 1],
        [0, 2]]))
torch.return_types.topk(
values=tensor([[0.7347, 0.2777],
        [0.7895, 0.7085]]),
indices=tensor([[0, 1],
        [1, 2]]))

         讲解在源码已标识注释。

2.3.9 Tensor的三角函数

 

import torch
a = torch.zeros(2, 3)
b = torch.cos(a)
print(a)
print(b)

         cos0=1。

2.3.10 Tensor中其他的数学函数

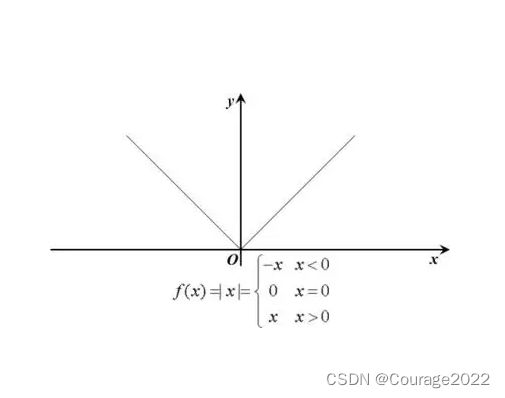
         最重要的就是绝对值函数、符号函数、sigmoid函数（激活函数）！