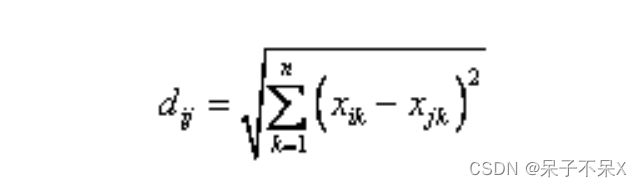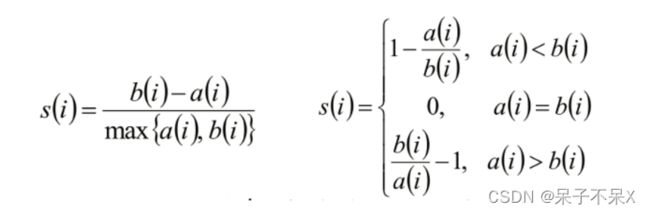机器学习 —— 聚类算法
K均值算法(K-means)聚类
一、K-means算法原理
聚类的概念:一种无监督的学习,事先不知道类别,自动将相似的对象归到同一个簇中。
K-Means算法是一种聚类分析(cluster analysis)的算法,其主要是来计算数据聚集的算法,主要通过不断地取离种子点最近均值的算法。
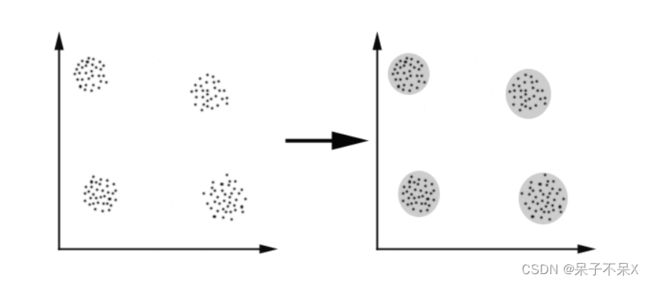
K-Means算法主要解决的问题如下图所示。我们可以看到,在图的左边有一些点,我们用肉眼可以看出来有四个点群,但是我们怎么通过计算机程序找出这几个点群来呢?于是就出现了我们的K-Means算法
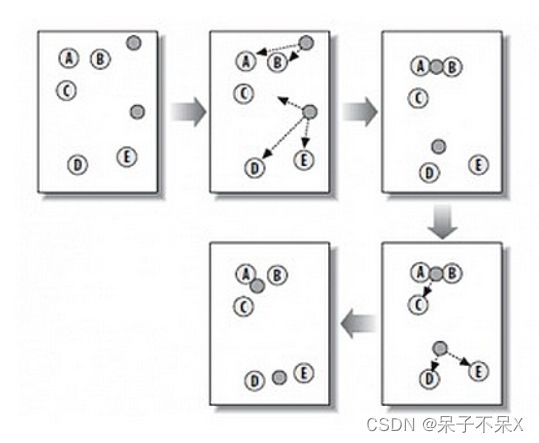
这个算法其实很简单,如下图所示:
从上图中,我们可以看到,A,B,C,D,E是五个在图中点。而灰色的点是我们的种子点,也就是我们用来找点群的点。有两个种子点,所以K=2。
然后,K-Means的算法如下:
- 随机在图中取K(这里K=2)个种子点。
- 然后对图中的所有点求到这K个种子点的距离,假如点Pi离种子点Si最近,那么Pi属于Si点群。(上图中,我们可以看到A,B属于上面的种子点,C,D,E属于下面中部的种子点)
- 接下来,我们要移动种子点到属于他的“点群”的中心。(见图上的第三步)
- 然后重复第2)和第3)步,直到,种子点没有移动(我们可以看到图中的第四步上面的种子点聚合了A,B,C,下面的种子点聚合了D,E)。
这个算法很简单,重点说一下“求点群中心的算法”:欧氏距离(Euclidean Distance):差的平方和的平方根
K-Means主要最重大的缺陷——都和初始值有关:
K是事先给定的,这个K值的选定是非常难以估计的。很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适。(ISODATA算法通过类的自动合并和分裂,得到较为合理的类型数目K)
K-Means算法需要用初始随机种子点来搞,这个随机种子点太重要,不同的随机种子点会有得到完全不同的结果。(K-Means++算法可以用来解决这个问题,其可以有效地选择初始点)
总结:K-Means算法步骤:
- 从数据中选择k个对象作为初始聚类中心;
- 计算每个聚类对象到聚类中心的距离来划分;
- 再次计算每个聚类中心
- 计算标准测度函数,直到达到最大迭代次数,则停止,否则,继续操作。
- 确定最优的聚类中心
二、实战
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline1、聚类实例
导包,使用make_blobs生成随机点
- from sklearn.datasets import make_blobs
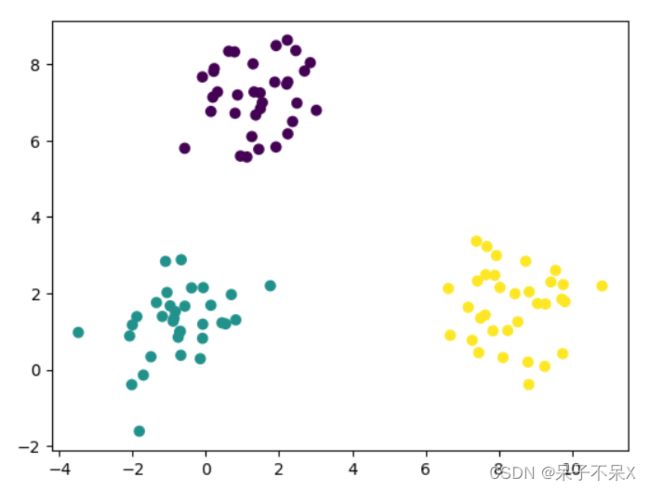
from sklearn.datasets import make_blobs
data,target = make_blobs()
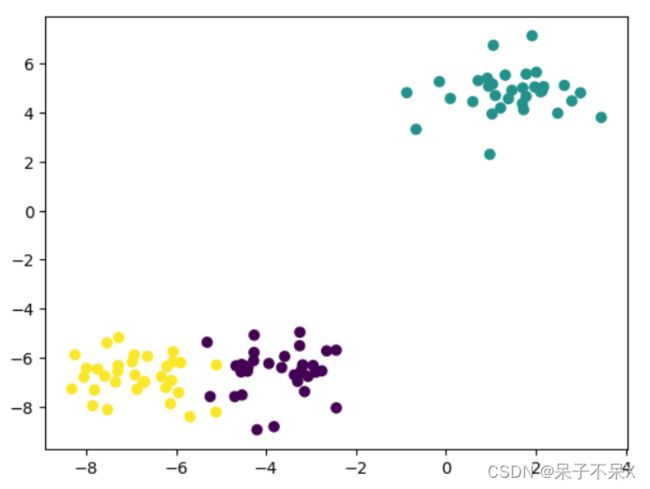
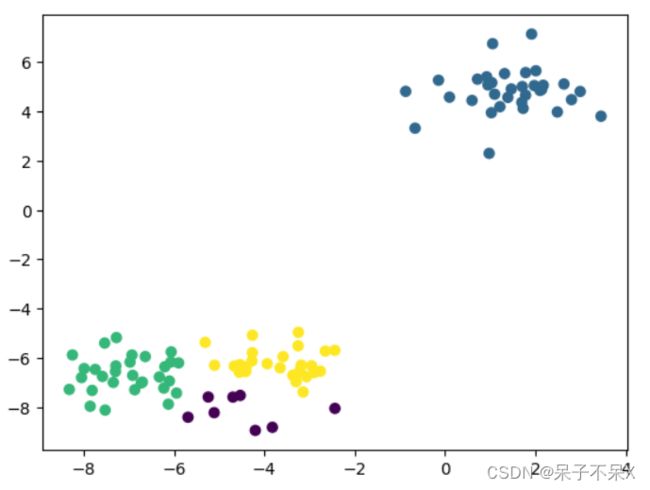
plt.scatter(data[:,0],data[:,1],c=target)建立模型,训练数据,并进行数据预测,使用相同数据
无监督的情况下进行计算,预测 现在机器学习没有目标
- from sklearn.cluster import KMeans, DBSCAN
# cluster : 聚类
from sklearn.cluster import KMeans, DBSCAN
# 创建
# n_clusters=8 : 默认8个组(簇),k = 8
kmeans = KMeans(n_clusters=4)
# 训练
# 聚类算法:不需要提供 target
kmeans.fit(data)labels_ : 每个样本点的标签
kmeans.labels_
'''
array([3, 3, 2, 0, 2, 0, 2, 2, 1, 3, 2, 3, 3, 1, 1, 2, 2, 0, 3, 3, 3, 1,
1, 2, 1, 2, 0, 3, 1, 3, 3, 1, 2, 3, 2, 1, 1, 3, 1, 1, 1, 3, 2, 1,
1, 1, 2, 1, 2, 2, 1, 3, 2, 2, 1, 1, 1, 3, 3, 3, 2, 1, 2, 3, 2, 1,
3, 1, 2, 3, 1, 3, 2, 1, 1, 3, 0, 1, 2, 2, 1, 1, 0, 0, 1, 3, 2, 2,
1, 2, 3, 3, 3, 3, 2, 3, 0, 1, 2, 2])
'''
plt.scatter(data[:,0],data[:,1],c=kmeans.labels_)重要参数:
- n_clusters:聚类的个数
重要属性:
- cluster_centers_ : [n_clusters, n_features]的数组,表示聚类中心点的坐标
- labels_ : 每个样本点的标签
# 分组的个数
kmeans.n_clusters
# 4
# 聚类中心
kmeans.cluster_centers_
'''
array([[-4.46626315, -8.14085978],
[ 1.44224349, 4.81770399],
[-7.01852833, -6.6710513 ],
[-3.74353854, -6.23186778]])
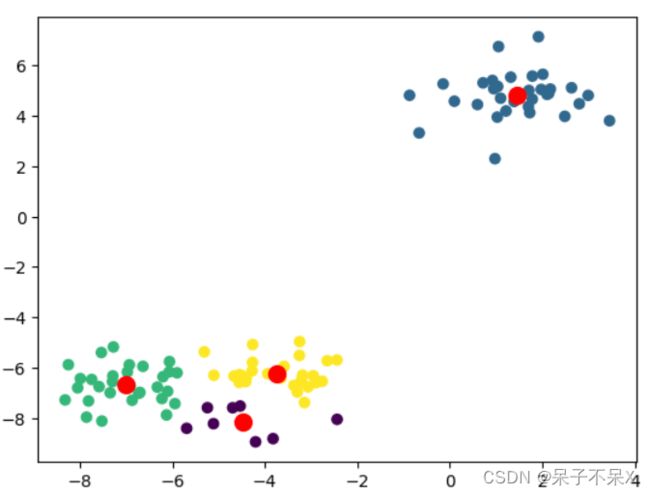
'''绘制图形中心点,显示聚类结果kmeans.cluster_centers
plt.scatter(data[:,0],data[:,1],c=kmeans.labels_)
# 话聚类中心
plt.scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],c='r',s=100)2、 实战,三问中国足球几多愁?
读取数据
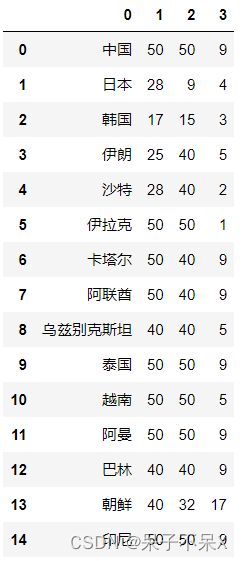
football = pd.read_csv('../data/AsiaFootball.txt',header=None)
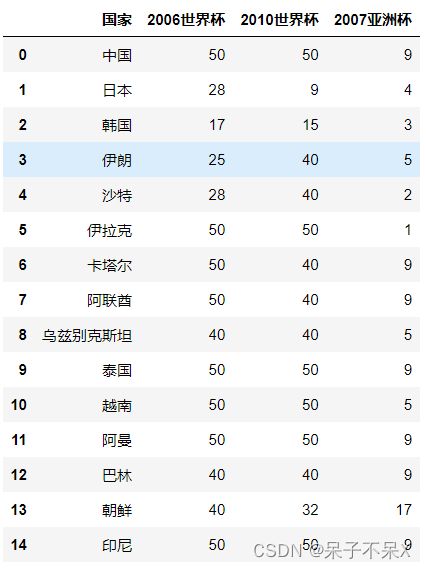
football列名修改为:"国家","2006世界杯","2010世界杯","2007亚洲杯"
football.columns = ["国家","2006世界杯","2010世界杯","2007亚洲杯"]
footballdata = football.iloc[:,1:].copy()使用K-Means进行数据处理,对亚洲球队进行分组,分三组
kmeans = KMeans(n_clusters=3)
kmeans.fit(data)
# labels
kmeans.labels_
# array([0, 1, 1, 2, 2, 0, 0, 0, 2, 0, 0, 0, 2, 2, 0])
country = football['国家'].values
country
'''
array(['中国', '日本', '韩国', '伊朗', '沙特', '伊拉克', '卡塔尔', '阿联酋', '乌兹别克斯坦', '泰国',
'越南', '阿曼', '巴林', '朝鲜', '印尼'], dtype=object)
'''for循环打印输出分组后的球队
0 == kmeans.labels_
'''
array([ True, False, False, False, False, True, True, True, False,
True, True, True, False, False, True])
'''
country[0 == kmeans.labels_]
'''
array(['中国', '伊拉克', '卡塔尔', '阿联酋', '泰国', '越南', '阿曼', '印尼'], dtype=object)
'''
for i in range(3):
print(country[i == kmeans.labels_])
'''
['中国' '伊拉克' '卡塔尔' '阿联酋' '泰国' '越南' '阿曼' '印尼']
['日本' '韩国']
['伊朗' '沙特' '乌兹别克斯坦' '巴林' '朝鲜']
'''
3、K-Means图片颜色点分类
- from sklearn.datasets import load_sample_image
- load_sample_image()
from sklearn.datasets import load_sample_image
china = load_sample_image('china.jpg')
plt.imshow(china)
flower = load_sample_image('flower.jpg')
plt.imshow(flower)china
'''
array([[[174, 201, 231],
[174, 201, 231],
[174, 201, 231],
...,
[250, 251, 255],
[250, 251, 255],
[250, 251, 255]],
[[172, 199, 229],
[173, 200, 230],
[173, 200, 230],
...,
[251, 252, 255],
[251, 252, 255],
[251, 252, 255]],
[[174, 201, 231],
[174, 201, 231],
[174, 201, 231],
...,
[252, 253, 255],
[252, 253, 255],
[252, 253, 255]],
...,
[[ 88, 80, 7],
[147, 138, 69],
[122, 116, 38],
...,
[ 39, 42, 33],
[ 8, 14, 2],
[ 6, 12, 0]],
[[122, 112, 41],
[129, 120, 53],
[118, 112, 36],
...,
[ 9, 12, 3],
[ 9, 15, 3],
[ 16, 24, 9]],
[[116, 103, 35],
[104, 93, 31],
[108, 102, 28],
...,
[ 43, 49, 39],
[ 13, 21, 6],
[ 15, 24, 7]]], dtype=uint8)
'''
china.shape
# (427, 640, 3)
保留主要的颜色,使用聚类成64种
- kmeans = KMeans(64)
- kmeans.fit(data)
kmeans = KMeans(64)
# %time kmeans.fit(china.reshape(-1,3))
# 计算量较大,速度很慢随机获取1000个图片中的颜色, 进行训练
data = china.reshape(-1,3)
data.shape
# (273280, 3)
# pd.DataFrame(data).sample(1000)
from sklearn.utils import shuffle
# 先打乱顺序,然后取1000个
data2= data.copy()
data3 = shuffle(data2)[:1000]
data3
'''
array([[248, 249, 254],
[ 63, 80, 36],
[235, 243, 254],
...,
[ 15, 26, 9],
[101, 102, 94],
[ 94, 104, 67]], dtype=uint8)
'''
data3.shape
# (1000, 3)
使用KMeans进行聚类
kmeans = KMeans(64)
# 训练
kmeans.fit(data3)
#labels
labels = kmeans.labels_
labels
'''
array([40, 58, 37, 10, 36, 28, 5, 55, 40, 58, 48, 38, 4, 14, 47, 14, 1,
15, 29, 56, 49, 35, 19, 17, 14, 36, 47, 33, 49, 2, 62, 17, 40, 47,
40, 37, 40, 17, 17, 24, 57, 10, 28, 14, 55, 0, 14, 13, 34, 35, 3,
17, 36, 3, 58, 44, 17, 57, 35, 40, 14, 56, 17, 10, 30, 4, 6, 23,
31, 0, 43, 30, 36, 39, 35, 11, 55, 11, 11, 37, 40, 35, 48, 19, 17,
63, 16, 1, 47, 58, 5, 10, 36, 30, 63, 6, 0, 4, 24, 3, 41, 47,
3, 0, 46, 8, 31, 49, 38, 37, 36, 55, 27, 57, 6, 14, 0, 5, 50,
55, 4, 28, 23, 14, 49, 17, 5, 7, 52, 37, 24, 23, 49, 46, 9, 17,
39, 42, 14, 58, 0, 6, 37, 7, 14, 17, 19, 51, 14, 45, 5, 55, 10,
49, 0, 50, 13, 38, 17, 10, 49, 13, 44, 58, 6, 3, 45, 9, 0, 52,
40, 17, 58, 0, 14, 30, 63, 57, 35, 35, 0, 41, 11, 40, 10, 22, 50,
47, 47, 10, 17, 51, 32, 3, 37, 7, 38, 14, 63, 37, 40, 35, 40, 52,
0, 11, 28, 17, 54, 31, 37, 52, 63, 35, 14, 5, 9, 47, 10, 11, 17,
17, 5, 11, 49, 6, 2, 10, 46, 0, 55, 40, 10, 52, 37, 49, 14, 35,
30, 37, 52, 4, 9, 3, 52, 48, 24, 7, 25, 56, 13, 29, 12, 48, 49,
0, 48, 35, 35, 0, 49, 41, 44, 19, 5, 10, 20, 47, 32, 0, 41, 47,
39, 28, 34, 5, 26, 40, 17, 28, 58, 37, 8, 19, 42, 40, 37, 24, 31,
56, 37, 6, 42, 59, 29, 47, 37, 63, 58, 34, 37, 16, 29, 41, 17, 44,
47, 58, 51, 17, 3, 4, 0, 10, 44, 57, 14, 36, 4, 24, 30, 5, 37,
30, 34, 11, 8, 0, 17, 51, 7, 34, 37, 19, 6, 4, 24, 63, 50, 40,
2, 0, 37, 26, 36, 28, 34, 2, 39, 47, 16, 26, 32, 10, 2, 40, 6,
39, 8, 37, 17, 43, 11, 28, 41, 7, 13, 35, 38, 49, 50, 50, 4, 31,
53, 40, 43, 39, 53, 3, 48, 0, 37, 24, 62, 55, 6, 3, 28, 55, 41,
31, 27, 10, 46, 0, 14, 1, 40, 34, 0, 14, 20, 56, 63, 40, 11, 0,
2, 0, 33, 55, 3, 63, 37, 49, 10, 49, 35, 32, 35, 4, 46, 30, 14,
28, 17, 13, 37, 37, 35, 43, 13, 35, 60, 29, 60, 7, 63, 50, 10, 35,
24, 11, 55, 55, 11, 56, 16, 42, 24, 31, 17, 11, 63, 14, 16, 37, 29,
47, 43, 41, 35, 52, 37, 38, 58, 14, 63, 47, 3, 39, 6, 34, 41, 30,
51, 55, 46, 3, 10, 4, 5, 63, 14, 0, 5, 47, 40, 2, 47, 58, 17,
38, 33, 38, 34, 2, 49, 17, 37, 63, 35, 35, 63, 7, 45, 28, 60, 0,
51, 35, 14, 5, 48, 14, 40, 47, 52, 58, 35, 57, 56, 62, 40, 17, 5,
21, 0, 55, 1, 63, 56, 14, 28, 5, 28, 0, 2, 61, 33, 5, 38, 35,
17, 3, 51, 14, 17, 6, 56, 9, 0, 24, 55, 40, 44, 5, 37, 0, 10,
13, 8, 60, 5, 38, 38, 60, 28, 2, 4, 17, 40, 27, 55, 62, 7, 12,
7, 4, 51, 11, 25, 28, 5, 41, 49, 0, 50, 28, 49, 9, 5, 30, 51,
37, 6, 14, 51, 53, 0, 49, 14, 17, 20, 28, 63, 0, 22, 3, 10, 2,
35, 6, 24, 55, 40, 37, 5, 14, 40, 0, 5, 40, 47, 40, 39, 17, 0,
49, 11, 6, 33, 5, 63, 34, 31, 31, 49, 19, 41, 6, 11, 31, 37, 6,
40, 38, 27, 37, 49, 63, 21, 30, 17, 25, 33, 17, 55, 31, 51, 34, 6,
24, 51, 7, 18, 40, 40, 27, 28, 18, 48, 47, 28, 40, 1, 27, 0, 29,
14, 28, 5, 11, 10, 39, 17, 47, 55, 39, 3, 48, 17, 1, 49, 22, 14,
13, 56, 16, 29, 35, 33, 7, 34, 40, 34, 28, 0, 54, 56, 14, 37, 11,
6, 0, 63, 63, 11, 51, 3, 14, 20, 40, 2, 38, 14, 29, 48, 28, 21,
0, 11, 25, 19, 24, 34, 14, 40, 0, 35, 2, 6, 56, 55, 40, 11, 44,
55, 57, 2, 14, 58, 31, 50, 10, 63, 48, 40, 52, 34, 59, 5, 48, 17,
55, 39, 0, 10, 26, 34, 27, 47, 37, 10, 17, 5, 50, 37, 37, 49, 19,
5, 11, 6, 37, 10, 15, 19, 53, 26, 55, 17, 17, 48, 14, 14, 47, 14,
48, 49, 14, 11, 7, 24, 13, 63, 44, 10, 29, 41, 55, 28, 49, 31, 58,
11, 17, 22, 29, 2, 53, 14, 58, 38, 37, 40, 49, 63, 17, 61, 18, 31,
14, 37, 17, 6, 24, 26, 38, 5, 47, 37, 31, 3, 11, 32, 7, 51, 37,
63, 37, 40, 43, 37, 34, 55, 39, 14, 17, 28, 22, 46, 14, 14, 37, 63,
28, 9, 10, 14, 10, 37, 48, 0, 29, 37, 48, 53, 16, 44, 14, 55, 17,
55, 34, 3, 40, 40, 17, 9, 17, 11, 6, 0, 4, 3, 47, 33, 10, 45,
48, 30, 29, 56, 24, 9, 0, 0, 9, 28, 34, 37, 40, 0, 63, 6, 40,
38, 22, 22, 34, 35, 58, 11, 48, 11, 17, 37, 11, 6, 14, 4, 35, 0,
36, 28, 13, 37, 55, 14, 4, 50, 46, 0, 0, 49, 48, 14, 13, 37, 31,
48, 24, 0, 63, 14, 10, 51, 31, 40, 10, 11, 20, 10, 47, 31, 47, 8,
14, 52, 5, 4, 14, 18, 57, 63, 0, 50, 44, 47, 21, 56, 59, 54, 32,
17, 14, 5, 45, 11, 49, 6, 48, 63, 53, 45, 28, 26, 38])
'''
# 聚类中心
centers = kmeans.cluster_centers_
centers
'''
array([[241.42 , 246.04 , 253.34 ],
[ 66.33333333, 95.66666667, 95. ],
[ 49.06666667, 25. , 22.46666667],
[180.7 , 191.55 , 188.2 ],
[123.52941176, 111.64705882, 92.58823529],
[ 47.26666667, 48.93333333, 36.6 ],
[205.76923077, 226.88461538, 249.65384615],
[ 84.78571429, 74.64285714, 56.64285714],
[218.33333333, 175.33333333, 136.16666667],
[146.8 , 156.1 , 162.3 ],
[209.65625 , 209.34375 , 214.59375 ],
[ 14.06451613, 13.12903226, 6.96774194],
[218.5 , 119.5 , 106. ],
[107.41666667, 110.08333333, 45.75 ],
[186.38888889, 210.09259259, 236.55555556],
[209. , 95. , 33.5 ],
[111.28571429, 47.28571429, 28.14285714],
[220.40816327, 236.42857143, 252.53061224],
[157.5 , 128.75 , 106.75 ],
[149.5 , 142. , 130.8 ],
[248.6 , 169.4 , 105.8 ],
[167. , 154.5 , 85.25 ],
[ 33. , 68.85714286, 73. ],
[ 80. , 15.33333333, 4.66666667],
[ 86.38888889, 86.22222222, 32.27777778],
[237.25 , 199.75 , 172.5 ],
[102.57142857, 104. , 96.14285714],
[172.57142857, 161.71428571, 134.28571429],
[ 23.64285714, 27.14285714, 16.28571429],
[170.76923077, 183.46153846, 175.07692308],
[123.25 , 126.16666667, 113.91666667],
[ 57.77777778, 53.94444444, 48.5 ],
[170.83333333, 97.16666667, 81.5 ],
[119.25 , 74.625 , 42.75 ],
[193.4 , 203. , 205.35 ],
[200.06896552, 211.51724138, 225.72413793],
[137.66666667, 140.33333333, 81.11111111],
[231.72 , 242.08 , 253.46 ],
[ 99.64705882, 96.58823529, 65.64705882],
[219.25 , 223.58333333, 225.83333333],
[249.93181818, 250.47727273, 253.84090909],
[ 75.08333333, 79.66666667, 73.66666667],
[145.75 , 59.25 , 48.25 ],
[193.66666667, 146.83333333, 109.33333333],
[ 84.6 , 40.5 , 31.3 ],
[198.83333333, 126.16666667, 85.66666667],
[ 18.25 , 46.75 , 45.75 ],
[ 35.67857143, 36.35714286, 26.10714286],
[ 4.66666667, 3.33333333, 1.42857143],
[240.03571429, 239.89285714, 241.92857143],
[152.5 , 171.58333333, 181.5 ],
[ 65.86666667, 69.6 , 53.66666667],
[123.27272727, 119.54545455, 61.18181818],
[ 50.57142857, 46.28571429, 9.28571429],
[164. , 83.66666667, 57.66666667],
[230.10714286, 232.53571429, 237.71428571],
[ 40.42857143, 12.28571429, 11.78571429],
[131.875 , 152. , 139.5 ],
[ 67.47058824, 64.94117647, 23.35294118],
[104. , 102.33333333, 18.66666667],
[104.6 , 117.2 , 118.4 ],
[165.5 , 182.5 , 100.5 ],
[131.75 , 87.75 , 78.75 ],
[194.43333333, 218.43333333, 244.86666667]])
'''
centers.shape, labels.shape
# ((64, 3), (1000,))
# 预测
y_pred = kmeans.predict(data)
y_pred.shape
# (273280,)
y_pred
# array([14, 14, 14, ..., 5, 11, 11])上面已经对 27万个 像素值 预测出了结果,结果的范围是0~63,共64组
接下来,我们用64个聚类中心点,分布替换每一个分组的所有像素值
plt.imshow(china)
centers.shape
# (64, 3)
centers[y_pred].shape
# (273280, 3)
# 新图
new_china = centers[y_pred].reshape(427,640,3)
new_china
'''
array([[[186.38888889, 210.09259259, 236.55555556],
[186.38888889, 210.09259259, 236.55555556],
[186.38888889, 210.09259259, 236.55555556],
...,
[249.93181818, 250.47727273, 253.84090909],
[249.93181818, 250.47727273, 253.84090909],
[249.93181818, 250.47727273, 253.84090909]],
[[186.38888889, 210.09259259, 236.55555556],
[186.38888889, 210.09259259, 236.55555556],
[186.38888889, 210.09259259, 236.55555556],
...,
[249.93181818, 250.47727273, 253.84090909],
[249.93181818, 250.47727273, 253.84090909],
[249.93181818, 250.47727273, 253.84090909]],
[[186.38888889, 210.09259259, 236.55555556],
[186.38888889, 210.09259259, 236.55555556],
[186.38888889, 210.09259259, 236.55555556],
...,
[249.93181818, 250.47727273, 253.84090909],
[249.93181818, 250.47727273, 253.84090909],
[249.93181818, 250.47727273, 253.84090909]],
...,
[[ 86.38888889, 86.22222222, 32.27777778],
[137.66666667, 140.33333333, 81.11111111],
[107.41666667, 110.08333333, 45.75 ],
...,
[ 35.67857143, 36.35714286, 26.10714286],
[ 14.06451613, 13.12903226, 6.96774194],
[ 4.66666667, 3.33333333, 1.42857143]],
[[107.41666667, 110.08333333, 45.75 ],
[123.27272727, 119.54545455, 61.18181818],
[107.41666667, 110.08333333, 45.75 ],
...,
[ 14.06451613, 13.12903226, 6.96774194],
[ 14.06451613, 13.12903226, 6.96774194],
[ 23.64285714, 27.14285714, 16.28571429]],
[[107.41666667, 110.08333333, 45.75 ],
[104. , 102.33333333, 18.66666667],
[104. , 102.33333333, 18.66666667],
...,
[ 47.26666667, 48.93333333, 36.6 ],
[ 14.06451613, 13.12903226, 6.96774194],
[ 14.06451613, 13.12903226, 6.96774194]]])
'''
plt.imshow(new_china / 255)
DBSCAN聚类算法
导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.cluster import KMeans, DBSCAN生成数据make_blobs()
- from sklearn.datasets import make_blobs
from sklearn.datasets import make_blobs
data,target = make_blobs()
plt.scatter(data[:,0],data[:,1],c=target)使用DBSCAN
# eps:半径
# min_samples:形成组(簇)的最小样本数
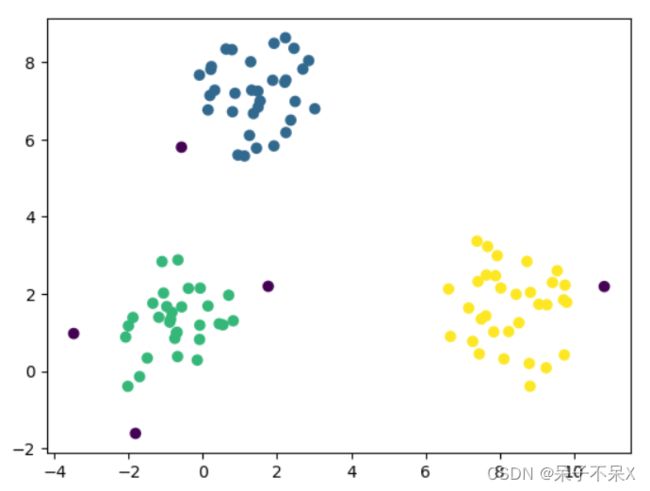
dbscan = DBSCAN(eps=1,min_samples=3)
dbscan.fit(data)
# 标签,分组结果
dbscan.labels_
# -1:离群点/噪声点
'''
array([ 0, 0, 1, -1, 0, 1, 2, 2, 1, 0, 2, 1, 2, 1, 0, 1, 2,
0, 0, 2, 0, 0, 2, 0, 2, 1, 2, 0, 0, 2, 1, 2, 2, 2,
2, 2, 1, 2, 1, 2, 2, -1, 0, 0, 0, 1, 0, 0, 1, 0, 2,
0, 0, 0, 2, 1, -1, 2, 1, -1, 1, 0, 0, 0, 0, 1, 2, 0,
2, 1, 2, 2, 1, 1, 1, 0, 0, 2, 1, 2, 1, 2, 1, 1, 1,
0, 2, 0, 1, 1, 0, 1, 2, 1, 0, 2, -1, 1, 0, 2],
dtype=int64)
'''
plt.scatter(data[:,0],data[:,1],c=dbscan.labels_)分别使用KMeans和DBSCAN算法
画圆
- from sklearn.datasets import make_circles
- 使用make_circles()
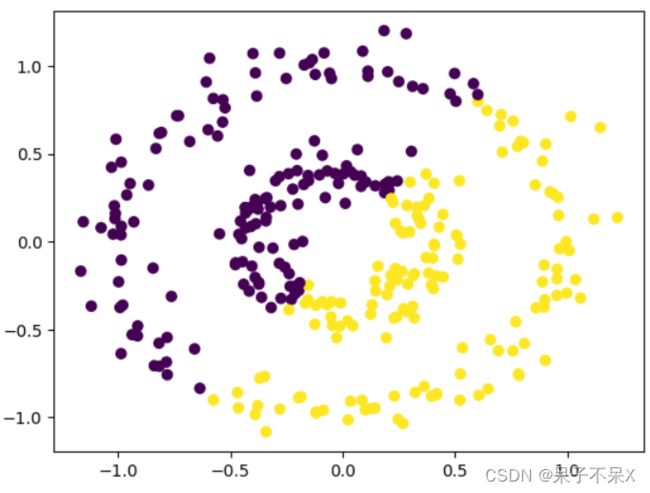
from sklearn.datasets import make_circles
# 画圆
data,target = make_circles(
n_samples=300, # 样本数
noise=0.09,# 噪声
factor=0.4,# 可理解为两堆点的离散程度,值小于 1
)
plt.figure(figsize=(6,6))
plt.scatter(data[:,0],data[:,1],c=target)
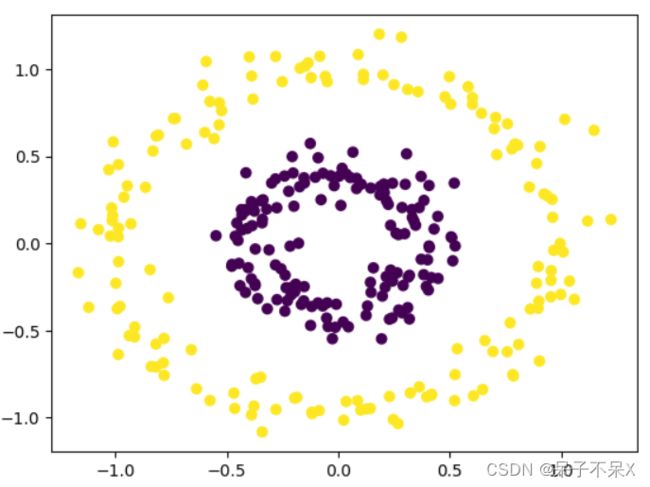
# 使用 DBSCAN
dbscan = DBSCAN(eps=0.2,min_samples=3)
dbscan.fit(data)
plt.scatter(data[:,0],data[:,1],c=dbscan.labels_)
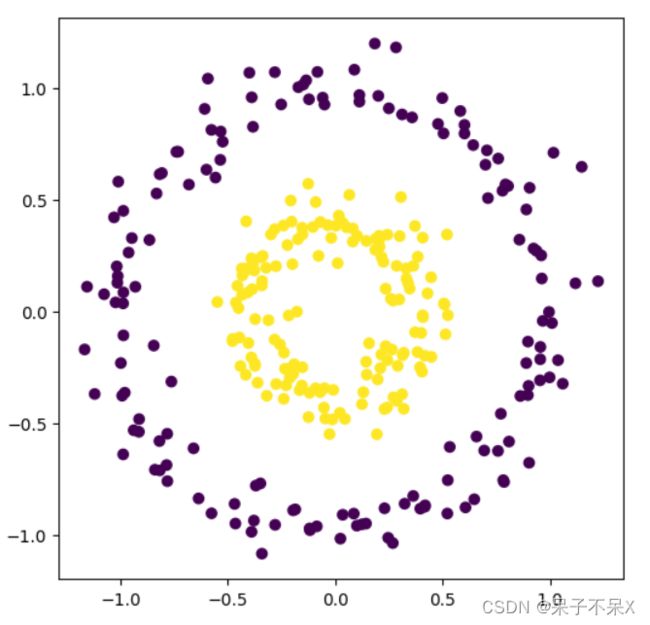
使用KMeans 查看效果区别
kmeans = KMeans(n_clusters=2)
kmeans.fit(data)
plt.scatter(data[:,0],data[:,1],c=kmeans.labels_)轮廓系数
聚类算法的评估指标,轮廓系数
聚类评估:轮廓系数(Silhouette Coefficient )
- 计算样本i到同簇其他样本的平均距离ai。ai 越小,说明样本i越应该被聚类到该簇。将ai 称为样本i的簇内不相似度。
- 计算样本i到其他某簇Cj 的所有样本的平均距离bij,称为样本i与簇Cj 的不相似度。定义为样本i的簇间不相似度:bi =min{bi1, bi2, ..., bik}
- si接近1,则说明样本i聚类合理
- si接近-1,则说明样本i更应该分类到另外的簇
- 若si 近似为0,则说明样本i在两个簇的边界上。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline加载数据
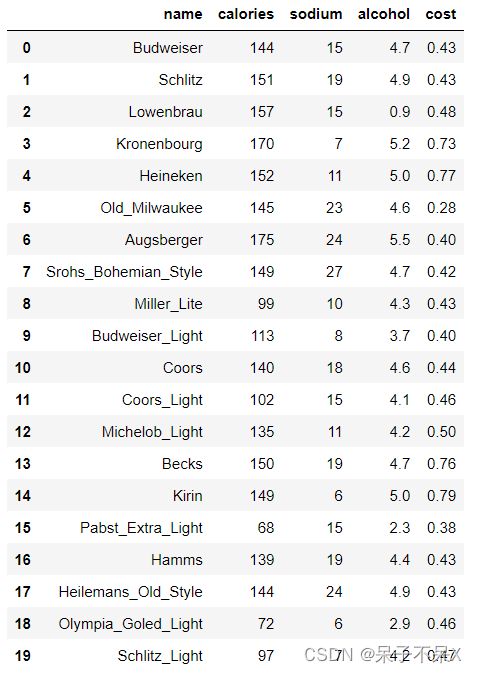
- beer.txt
beer = pd.read_table('../data/beer.txt',sep=' ')
beerdata = beer.iloc[:,1:].copy()导入KMeans
- from sklearn.cluster import KMeans, DBSCAN
from sklearn.cluster import KMeans, DBSCAN
kmeans = KMeans(n_clusters=4)
kmeans.fit(data)
kmeans.labels_
# array([0, 0, 0, 2, 0, 0, 2, 0, 1, 1, 0, 1, 0, 0, 0, 3, 0, 0, 3, 1])计算轮廓系数
- silhouette_samples: 每个样本的轮廓系数
- from sklearn.metrics import silhouette_samples
- 平均轮廓系数得分
- from sklearn.metrics import silhouette_score
from sklearn.metrics import silhouette_samples,silhouette_score
# silhouette_samples(data,kmeans.labels_)
'''
array([0.69616375, 0.59904896, 0.22209903, 0.33228274, 0.47164962,
0.6803127 , 0.41274592, 0.53937684, 0.73244266, 0.58828484,
0.70434972, 0.71134265, 0.52449913, 0.63186817, 0.45253349,
0.72050474, 0.6934216 , 0.66869429, 0.68369738, 0.64876323])
'''
silhouette_score(data,kmeans.labels_) # 平均轮廓系数
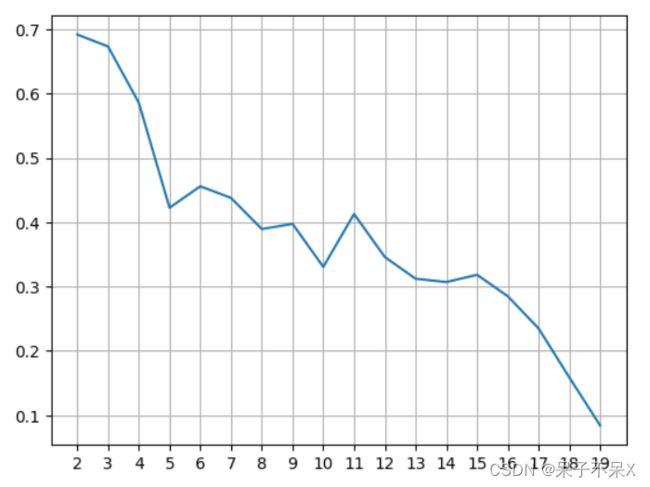
# 0.5857040721127795如何根据轮廓系数选择最合适的K
- 轮廓系数越大, K值越合适
# 提供不同的 K 值,分别计算轮廓系数
score_list = []
for k in range(2,20):
kmeans = KMeans(k)
kmeans.fit(data)
score = silhouette_score(data,kmeans.labels_)
# print(k,'得分',score)
score_list.append(score)
# 画图
plt.plot(range(2,20),score_list)
plt.xticks(range(2,20))
plt.grid()
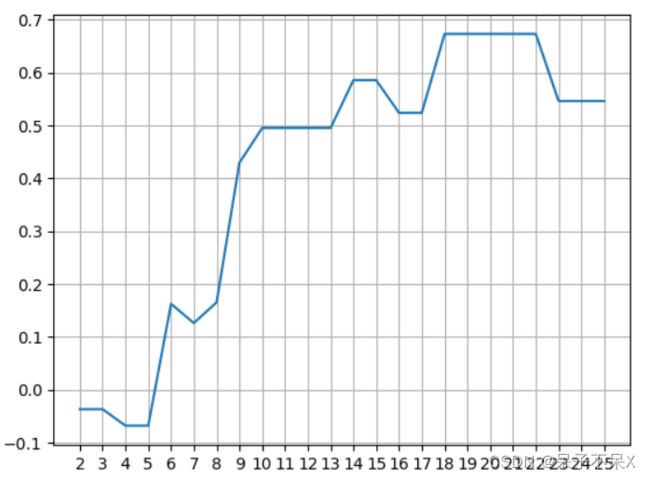
plt.show()DBSCAN使用轮廓系数
from sklearn.cluster import KMeans, DBSCAN
score_list = []
for eps in range(2,26):
dbscan = DBSCAN(eps=eps,min_samples=2)
dbscan.fit(data)
score = silhouette_score(data,dbscan.labels_)
score_list.append(score)
# 画图
plt.plot(range(2,26),score_list)
plt.xticks(range(2,26))
plt.grid()
plt.show()
# eps半径 = 18到22时轮廓系数最大