计算机图形学五:几何-Geometry
文章目录
- 几何(Geometry)
- 曲面(Curved Surface)
-
- 隐式曲面(Implicit Surface)
-
- 隐式曲面特点
- 代数曲面(Algebraic Surface)
- 构造固体几何(Constructive Solid Geometry)
- 符号距离函数(Signed Distance Function)
- 水平集(Level Set)
- 分型几何(Fractals)
- 显示曲面(Explicit Surface)
-
- 显示曲面特点
- 点云(Point Cloud)
- 多边形网格(Polygon Mesh)
- The Wavefront Object File(.obj)
- 曲线(Curve)
-
- 贝塞尔曲线(Bézier Curves)
- 贝塞尔曲面(Bézier Surfaces)
- 曲面细分(Mesh Subdivision)
-
- Loop细分(Loop Subdivision)
- Catmull-Clark细分(Catmull-Clark Subdivision)
- 曲面简化(Mesh Smplication)
几何(Geometry)
几何与计算机图形学密不可分,图形的表达、呈现等几乎都以几何形体的方式呈现。
例如水杯:

水滴:

建筑群:
几何的形状与多少决定了渲染的复杂程度,如何表示好各种各样的模型是几何部分的主要研究内容之一。俗话说点构线,线构面,面构体,而几何形体的最基本要素,就是曲线与曲面。
曲面(Curved Surface)
隐式曲面(Implicit Surface)
隐式曲面特点
所谓隐式曲面指的是并不会告诉你任何点的信息,只会告诉你该曲面上所有点满足的关系。来举个具体的隐式曲面的例子:
x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x2+y2+z2=1大部分人一眼就看出来这是一个3维球体的方程,一般地的我们会把隐式曲面的代数方程写作 f ( x , y , z ) = 0 f(x,y,z) = 0 f(x,y,z)=0,则该球体的隐式曲面方程表示为:
f ( x , y , z ) = x 2 + y 2 + z 2 − 1 f(x,y,z) = x^2 + y^2+z^2-1 f(x,y,z)=x2+y2+z2−1对于隐式方程来说因为没有给出任何点的信息,因此如何判断所给出的隐式方程描述的是一个怎样的形状十分困难,如下图这样一个例子:
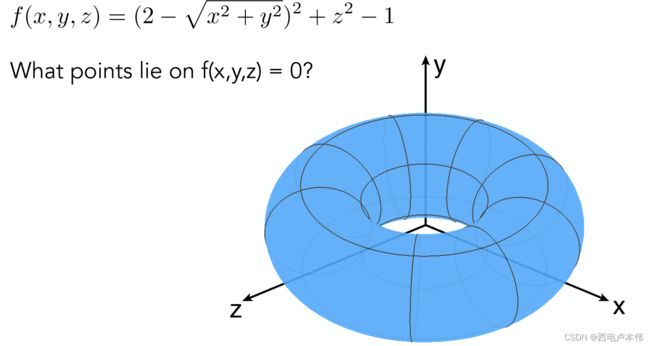
但是它也有好处:可以十分容易的判断出一点与曲面的关系,即我们可以将具体的点坐标代入方程,如果 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0,就说明该点是构成曲面的要素,如果 f ( x , y ) > 0 f(x,y)>0 f(x,y)>0,就说明该点在曲面外,相反的,如果 f ( x , y ) < 0 f(x,y)<0 f(x,y)<0,就说明该点在曲面内。

当然代数曲面只是隐式曲面的一种表现形式,接下来将会一一介绍隐式曲面的其他表现形式。
代数曲面(Algebraic Surface)
隐式曲面可以通过上述所介绍的代数表达式得到,可以得到许许多多不同的几何曲面:

但这种表达方式存在多种缺点,首先是只根据表达式大多数情况下根本无法确定所要表达的到底是什么模型,其次就是方程式大多只能表示规则的形状,如果是很复杂的形状的叠加又该怎么办呢?
构造固体几何(Constructive Solid Geometry)
Constructive Solid Geometry(CSG)指的是可以对各种不同的几何做布尔运算,如并,交,差:

通过这些操作可以得出各种更为复杂的几何:

通过CSG的方法可以一定程度上缓解隐式曲面难以表现复杂形体的困境。
符号距离函数(Signed Distance Function)
首先看这么一张图:

从左往右看,是两个球体慢慢混合(blend)至一个球体,可以从中间过程看出这种混合过程伴随这球体形体的变化,显得混合的十分自然真实,如何表达出这种曲面的变换呢?
符号距离函数(sign distance function),简称SDF,又可以称为定向距离函数(oriented distance function),在空间中的一个有限区域上确定一个点到区域边界的距离并同时对距离的符号进行定义:点在区域边界内部为正,外部为负,位于边界上时为0。
对,我们可以通过空间任意一点到各个几何物体表面的距离,对这些距离做各种各样的运算操作最后得到的一个最终的距离函数,举一个简单的例子:

对于这样一个二维平面,定义空间中每一个点的 S D F SDF SDF 为该点到阴影区域右边界的垂直距离,在阴影内部为负,外部为正,右边界即为形体表面,其上点 S D F SDF SDF 为0。因此对于 A 和 B 两种阴影来说的 S D F SDF SDF 分别如上图下半部分所示。有了 S D F ( A ) , S D F ( B ) SDF(A),SDF(B) SDF(A),SDF(B) 之后对这两个距离函数选择性的做一些运算得到最终的距离函数,这里采用最简单的 S D F = S D F ( A ) + S D F ( B ) SDF = SDF(A)+SDF(B) SDF=SDF(A)+SDF(B) 来表达混合这一变化,最终得到的 S D F SDF SDF 为零的点的集合即为混合之后曲面边界,对该例子来说,就是两道阴影之间中点的一条线:

即符号距离函数来表达隐式曲面的最基本思路是:根据 S D F SDF SDF 为0的点来描绘物体曲面。因此对于一开始的那个例子来说,只需合理定义空间中任意一个点的 S D F SDF SDF,再令 S D F SDF SDF 为0即可得到混合的效果了。
水平集(Level Set)
水平集的方法其实与 S D F SDF SDF 很像,也是找出函数值为0的地方作为曲线,但不像 S D F SDF SDF 会空间中的每一个点有一种严格的数学定义,而是对空间用一个个格子去近似一个函数(将距离存储在表格中),如下:

对该面内的每一个点利用已经定义好的格子值进行双线性插值(前一节纹理映射提到)就可以得到任意一点的函数值,找出所有值为0的点作为曲面。(类似于地理中的等高线??)
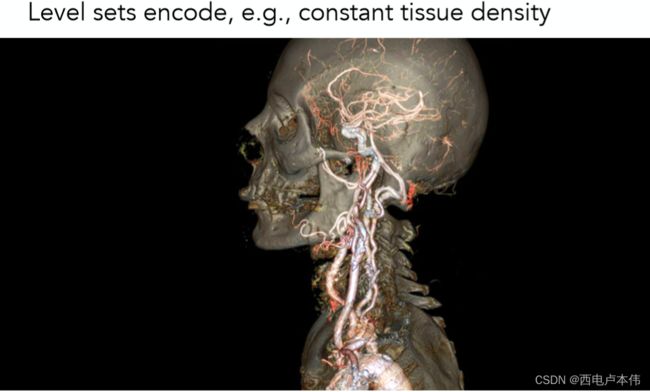
该方法的好处是对于 S D F SDF SDF,我们可以更加显示的区空间曲线的形状。该方法广泛的运用在医学成像和物理模拟之中,例如下图我们可以记录下人体组织表面的各个密度,根据组织密度相同的点进行连接绘制得到相应组织的大致形状:
分型几何(Fractals)
分型几何是指许许多多自相似的形体最终所组成的几何形状。
如雪花是一个六边形,放大之后会发现每一个边上又是一个六边形,再放大六边形边上的六边形边上又是六边形,就这样无限套娃,有点递归的意思。

综上,隐式曲面具有形式简单,轻易判断点与曲面关系等优点,但难以采样曲面点和模拟过于复杂的形状。
显示曲面(Explicit Surface)
显示曲面特点
对于显式曲面来说是与隐式曲面相对应的,所有曲面的点被直接给出,或者可以通过映射关系直接得到,如下图:

虽然没有直接给出点的数据 x , y , z x,y,z x,y,z,但是拥有 u , v u,v u,v 的取值范围以及从 $ (u,v)\rightarrow(x,y,z)$ 的映射关系,那么只需要将所有的 u , v u,v u,v 代入自然就可求得 x , y , z x,y,z x,y,z(类似于从texture到模型的映射)。例如:

我们可以很轻松的将所有的 u , v u,v u,v 代入自然就可求得 x , y , z x,y,z x,y,z,进而求得整个曲面。
区别隐式曲面与显示曲面的关键就在于是否可以直接表示出所有的点。隐式曲面难以采样曲面上的点,但是可以轻易判断点与曲面的关系,对于显式曲面来说恰恰相反,我们可以很轻易的采样到所有的点,但是给予你任意一点却很难判断它与曲面的关系。因此没有哪一种的几何表现方式是更好的,根据具体的环境条件来选择隐式还是显式才是合理的做法。
下面介绍几种显示曲面的表现形式:
点云(Point Cloud)
很多很多的点构成的曲面,直接有着所有点的信息,点多模型细节就多,点少模型细节就少。

多边形网格(Polygon Mesh)
最常用的曲面表现形式,简单来说通过定义各个多边形面的顶点以及顶点之间的连接关系就可以得到许许多多的三角形面或是四边形面,再通过这些面来近似表现出我们想要的模型效果。

The Wavefront Object File(.obj)
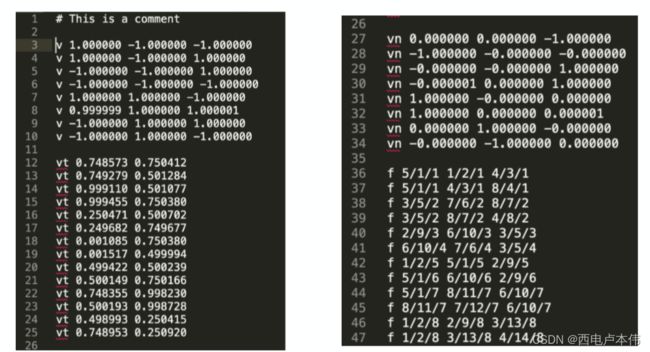
该形式就是利用文件存储几何的信息。例如一个立方体的模型数据例子,利用.obj文件才存储信息:
3-10行定义了立方体的8个顶点信息。
12-25行定义了这些顶点的纹理坐标信息(每个面4个点,共6个面所以最多有24种不同的纹理坐标信息,这里有一些纹理对于不同面上的点是公用的)。
27-34行定义了6个面的法线信息。
36-47行中, f f f 代表一个面,其中 x / x / x x/x/x x/x/x 的第一位表示是哪个顶点,第二位表示该顶点纹理坐标是第几个,第三位表示法线信息是第几个。 3个 x / x / x x/x/x x/x/x 表示3个顶点的信息构成一个三角形面。
曲线(Curve)
贝塞尔曲线(Bézier Curves)
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝塞尔曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。
贝塞尔曲线于1962,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发,以稳定数值的方法求出贝塞尔曲线。
首先看一下一条实际的贝塞尔曲线长什么样子:

其中 p 0 , p 1 , p 2 , p 3 p_0,p_1,p_2,p_3 p0,p1,p2,p3 为控制点,蓝色所表示曲线就是贝塞尔曲线了,可以从图中观察到,曲线会与初始与终止端点相切,并且经过起点 p 0 p_0 p0 与终点 p 3 p_3 p3。那么这样一条曲线究竟是怎么得到的呢?需要用到 Casteljau 算法。

首先从简单的3个控制点情形出发,示意如何画出曲线。(n个控制点得到的是n-1次曲线,如图中3个控制点便是2次贝塞尔曲线)
正如一开始所说,第一步选定一个时间参数 t ∈ [ 0 , 1 ] t\in[0,1] t∈[0,1],在 b 0 b 1 b_0b_1 b0b1 线段之上利用 t t t 值进行线性插值:

即 b 0 1 = b 0 + t ∗ ( b 1 − b 0 ) b_0^1 = b_0+t*(b_1-b_0) b01=b0+t∗(b1−b0),得到 b 0 1 b_0^1 b01 之后在 b 1 b 2 b_1b_2 b1b2 线段上重复做相同的线性插值得到点 b 1 1 b_1^1 b11:

通过给点参数 t t t 计算得到点 b 0 1 , b 1 1 b_0^1,b_1^1 b01,b11之后将两点连接,接下来如法炮制在 b 0 1 b 1 1 b_0^1b_1^1 b01b11 线段之上再进行一次线性插值:
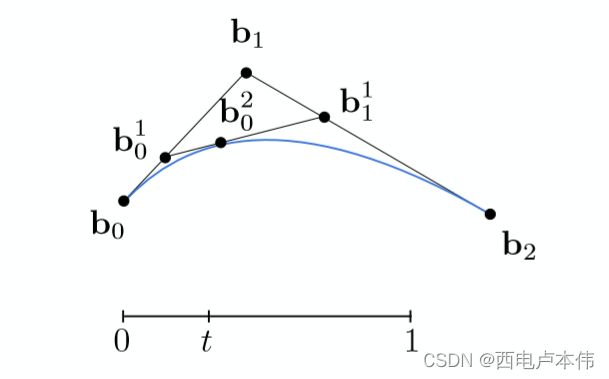
如此便成功获得了如图所示的3个控制点之下的2次贝塞尔曲线上的一点 b 0 2 b_0^2 b02了,那么对所有的 t ∈ [ 0 , 1 ] t\in[0,1] t∈[0,1] 都重复上述的过程,理论上就可以得到无数个位于贝塞尔曲线上的点,进而得到贝塞尔曲线了。通过这样一个简单的3个控制点的例子,相信很快就能理解贝塞尔曲线的原理,那么对于4个控制点,5个控制点,乃至任意控制点步骤都是类似的。其核心所在就是多次的线性插值,并在生成的新的顶点所连接构成的线段之上递归的执行这个过程,直到得到最后一个顶点
如下图这样一个4个控制顶点的例子,步骤完全类似:

当然这只是图形上的表示,如何定量表示呢?同样以一开始的3个控制点为例,利用二次插值的数学公式,将贝塞尔曲线方程展开看看:
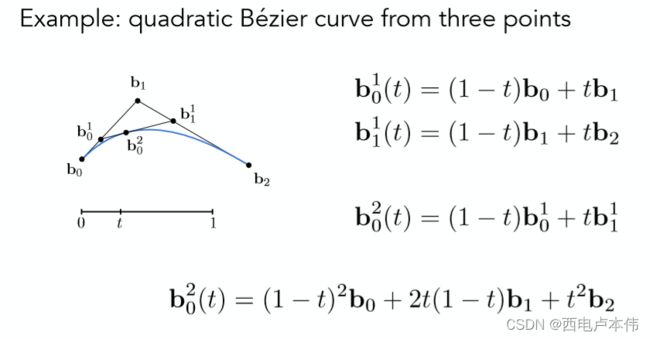
其实看到这就已经非常清楚了,最终得到的贝塞尔曲线方程恰好就是一个关于参数 t t t 的二次方程,如果细心观察的话,其实可以发现控制点的系数是非常有规律的,很像二项系数,因此可以总结规律得到一个任意控制点组成的贝塞尔曲线的方程如下:

对于这样一个特殊系数其实也有一个多项式与之对应,正是伯恩斯坦多项式(Bernstein polynomials),其定义如图中下方所示:
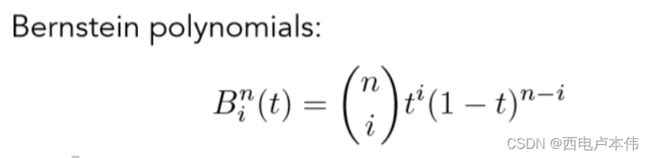
其实这就是多项式展开的那个系数,高中好像学过,我把它理解成这样:
B i n ( t ) = C n i t i ( 1 − t ) n − i B_i^n(t)=C_n^it^i(1-t)^{n-i} Bin(t)=Cniti(1−t)n−i其中 C n i C_n^i Cni 就是排列组合里面那个玩意儿。
贝塞尔曲线的定义以及数学表达都介绍了,最后对贝塞尔曲线的几点性质做一个概括:
- 必定经过起始与终止控制点
- 必定经与起始与终止线段相切
- 具有仿射变换性质,可以通过移动控制点移动整条曲线(简要来说,通过由控制点得到的贝塞尔曲线进行仿射变换与对控制点进行同样的仿射变换后得到的贝塞尔曲线是一样的)
- 凸包性质,曲线一定不会超出所有控制点构成的多边形范围
什么是凸包(convex hull)?想象墙上有许多图钉,我们需要用一根橡皮筋把这些图钉围住,于是我们开始会让橡皮筋尽可能的撑大,然后松手放开橡皮筋,它所形成的多边形即为凸包,如图中蓝色曲线所示:
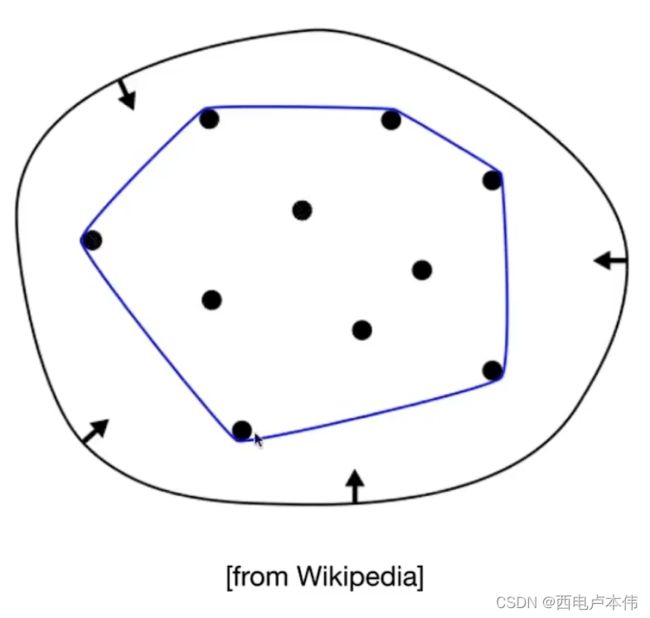
贝塞尔曲线是完美的吗?来看个有11个控制点的例子:
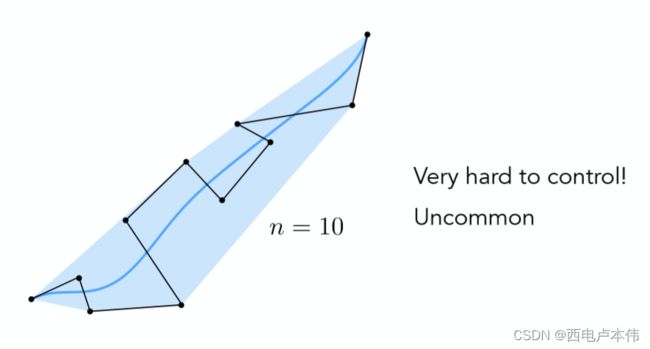
所得到的贝塞尔曲线是完全正确的,可总感觉怪怪的,在某些点感觉根本不受控制点的“控制”。这正是由于控制点众多,很难控制局部的贝塞尔曲线形状。为了解决该问题,有人提出了分段贝塞尔曲线,即将一条高次曲线分成多条低次曲线的拼接,其中用的最多的便是用很多的3次曲线(4个控制点)来拼接,如下图:
![]()
图中,①②③④点是第一段贝塞尔曲线的控制点,④⑤⑥⑦是第二段贝塞尔曲线的控制点,⑦⑧⑨⑩是第三段贝塞尔曲线的控制点,我们可以分段得到曲线之后连接。但这种表示方法也有很大的问题,如上图第二段与第三段曲线的连接点⑦处,曲线出现了非常大的偏转,如何在连接点处做到平滑的过度?
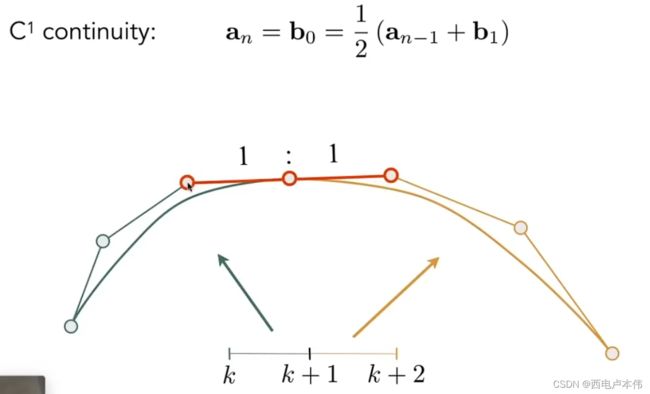
我们知道贝塞尔曲线的特点,必定经与起始与终止线段相切,如上图,第一段曲线的终点斜率同线段③④的斜率,而第二段曲线的起点斜率同线段④⑤的斜率,如果这两个线段的尾部和头部的斜率一样是否就能达到平滑的额效果呢,答案是肯定的。我们要做的是确保③⑤两个点在同一条直线上且③④长度等于④⑤长度。
最后要介绍一下贝塞尔曲线的连续性:
C 0 C^0 C0 连续性:第一段曲线的终点为第二段曲线的起点。
C 1 C^1 C1连续性:就是上述说到的平滑过渡。
贝塞尔曲线测试demo 挺好玩的,可以自己动手试试。
贝塞尔曲面(Bézier Surfaces)
其实在理解了贝塞尔曲线之后,贝塞尔曲面的原理也是十分容易理解的了,无非是一个从2维到3维的过渡。
如果说对于曲线来说只有一个参数 t ∈ [ 0 , 1 ] t\in[0,1] t∈[0,1] 那么对于一个面来说,就应该有两个参数,分别设 $ u\in[0,1] , , ,v\in[0,1]$,具体过程如下图所示:

举一个 4 ∗ 4 = 16 4*4 = 16 4∗4=16个控制点的例子,其水平面位置如图中16个黑点所示(并未表示出高度,防止图形太乱),将这16个点分成4列,图中红色圈中的为一列的具体例子。
第1步:在每列4个控制点之下利用第一个参数 u u u 运用计算贝塞尔曲线的方法得到空中的四条灰色贝塞尔曲线,同时可以得到同一个 u u u 下所示的4个蓝色点。
第2步:在得到4个蓝色顶点之后,在这四个蓝色顶点的基础之下利用第二个参数 v v v 便可以成功得出贝塞尔曲面上的正确一点
第3步:遍历所有的 u , v u,v u,v 值就可以成功得到一个贝塞尔曲面
曲面细分(Mesh Subdivision)
曲面细分是指将一个模型的面合理的分成更多小的面,从而提升模型精度,提高渲染效果,大白话就是将大三角形分成很多个小三角形。
 如何做呢?
如何做呢?
Loop细分(Loop Subdivision)
Loop细分(Loop是发明人的姓氏,不是循环的意思…)是一种专门针对三角形面的细分方法,其核心步骤:
生成更多的三角形跟点
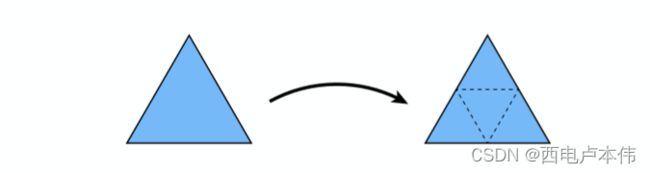
如图所示在连接每条边的中点生成一个新的三角形,原来的三角形就会被分割成4个三角形。
调整这些三角形或顶点的位置
图形的细分必然会导致位置的改变,如何合理更改位置使得模型更加美观是细分的第二步。我们将所有的顶点分为两类,一类是新生成的顶点,一类是老的原来就有的顶点,对于新生成的顶点做如下处理:

这里新的顶点就是白色的那个顶点,其位置为周围4个顶点的权重之和(具体推到属于数学领域,不做深究),各顶点权重如图所示,其余边上的新顶点处理类似。
对于旧的顶点,做如下处理:
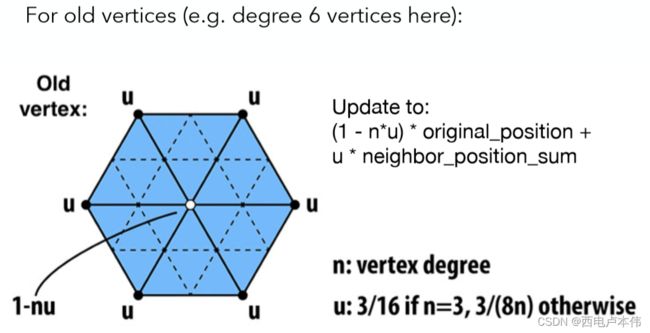
其实旧每个顶点的处理也十分类似,这里以图中一个白色旧顶点为例,也是其自身以及邻接顶点的权重和,但权重的设置与该旧顶点度数有关。其中 n n n 表示点的度数,学过数据结构的应该都知道度这个概念,就是与点相连的边的个数, u u u 跟新节点表示方法一样为权重。
Catmull-Clark细分(Catmull-Clark Subdivision)
Loop细分只能处理三角形面的细分,那么对于不仅仅只有三角形面该怎么办呢?这也就有了Catmull-Clark细分。
首先做一些定义:
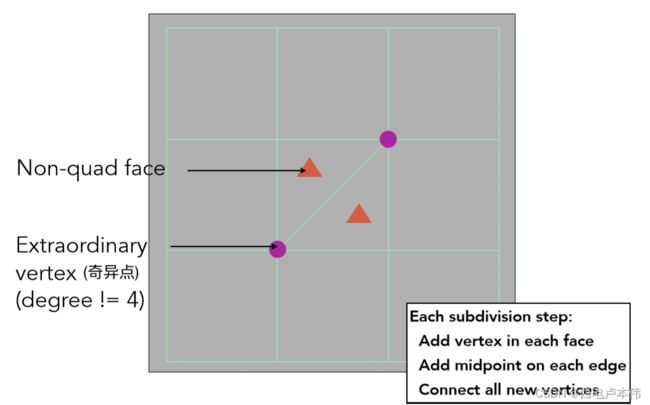
1. 对于所有不是四边形的面,称之为Non-quad face
2. 所有度不为4的顶点称之为奇异点,标记出来
3. 每次细分步骤如图中所示,在每个面中都添加一个点,在每条边的中点也都添加一个点,面上的新顶点连接所有边上的新顶点,进行四边形的细分。之后在每个Non-quad face中随便找一个点连接
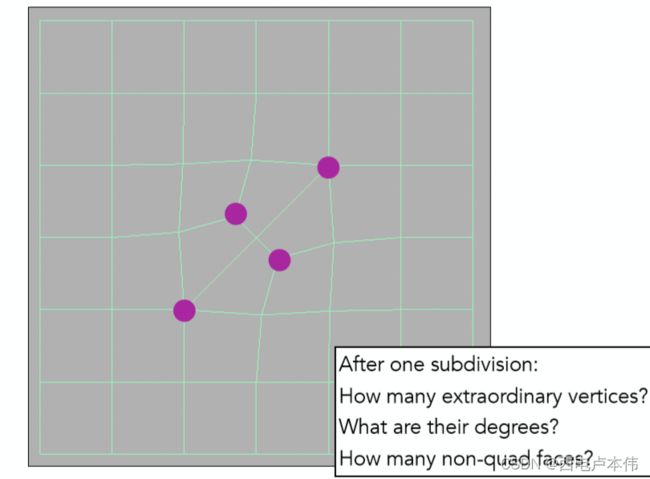
考虑右下角几个问题,其实也是一些Catmull-Clark细分的特点:
1. 有几个非四边形面,就会多出几个奇异点,所以现在一共有2+2 = 4个
2. 新多出来的奇异点的度数与原来所在面的边数相等,如这里就是3度
3. 第一次细分之后所有面都会变成四边形,且往后奇异点数目不再增加
这里给出一个再一次细分的结果:

可以看到奇异点依然是4个,不再改变。
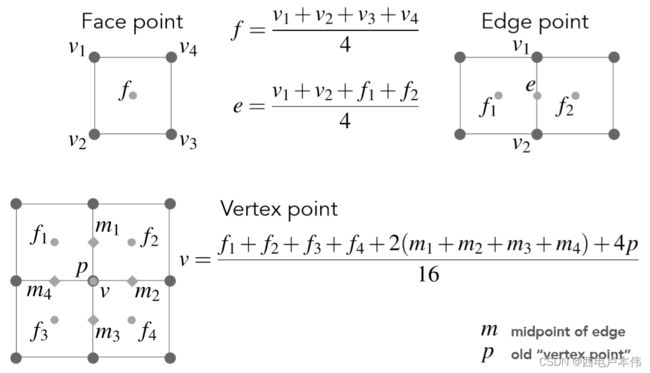
以上我们明白了如何增加新顶点,与Loop细分类似,同样需要去调整各类顶点的位置,这里将所有的顶点分为三类,对于各类顶点位置调整如下图所示:
下图是两种细分方法的效果对比:

曲面简化(Mesh Smplication)
为了得到更好的光滑模型,我们需要进行曲面细分。那为什么要曲面简化呢,那样不是让模型精度降低了吗。没错,要的就是模型精度降低的效果。

一方面,降低模型精度可以提高性能;另一方面,在某些情况下,我们根本就没有必要呈现那么完美的模型,例如:

在距离足够远的情况下,我们根本看不出来30000个三角形与3000个三角形的区别。换句话说,我们只需要在摄像机离模型十分近的情况下才需要展示精度高的模型,其他情况下适当降低精度可以大大提高计算机性能。
换个角度,这是否与纹理映射中Mipmap差不多呢?在某个像素点离摄像机十分远,这个点就会对应texture中十分大的一片区域,对应mipmap,我们并不需要用 Level 等级低的贴图去渲染。这个也类似,离摄像机十分远进行“模糊”是十分有必要的。
如何做呢?曲面简化所利用的一个方法叫做边坍缩(Edge collapse),如下图所示就是将一条边的两个顶点合成为一个顶点。但随之而来的问题就是,曲面简化需要尽量保持原本模型的shape,如何坍缩一条边,或者说坍缩哪一条边能够使得原模型样貌被改变的程度最小,这就是曲面简化的关键所在。
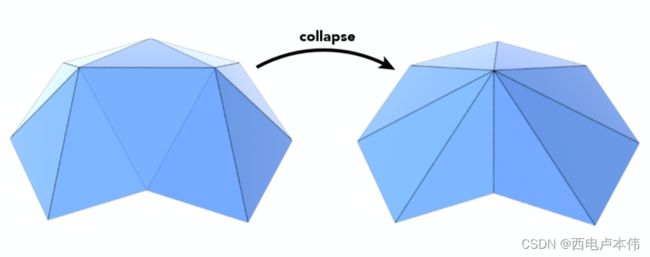
为此引入一个度量,即二次误差度量(Quadric Error Metrics)。
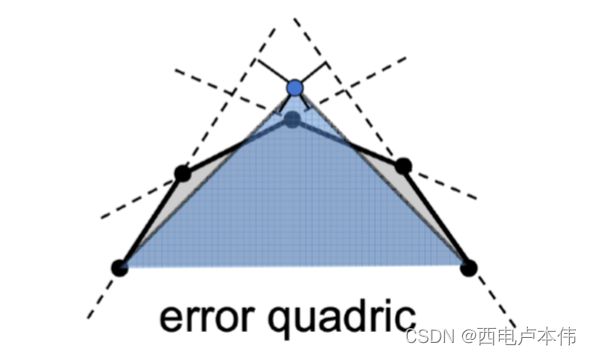
即坍缩之后蓝色新顶点所在的位置与原来各个平面的垂直距离之和。如果能够使得这个误差最小那么对整个模型样貌修改一定程度上也会较小。那么其实到这整个曲面简化的算法流程已经比较清晰了:
1. 为模型每条边赋值,其值为坍缩这条边之后,代替两个老顶点的新顶点所能得到的最小二次误差度量
2. 选取权值最小的边做坍缩,新顶点位置为原来计算得出使得二次误差最小的位置
3. 坍缩完之后,与之相连其他的边的位置会改动,更新这些边的权值
4. 重复上述步骤,直到到达终止条件


