第三届Python数据分析职业技能比赛A题

Hello World!

大家好！这里是一名练习时长两年半的大数据专业练习生，这一篇也是第一篇blog，来的实在是晚了些。平时没有记录的习惯，自然少了些分享的欲望。对于这次学校在期末举办的水友赛，由于种种原因没有呈交最后的论文，以至于在 “清灰” 时对这个文件夹里面的，几乎快无法辨认的代码感到非常惊讶。

回望那段被八篇结课论文追到美国人作息的生活，依然硬挤出来这份不那么完美的作品，相较于放假后我狂刷b站不理会老贾头的潇洒，着实显得可贵。

于是！我决定赶紧动一动我这刚勤劳一会就会僵硬滴小手，把完整的赛题、思路、代码放上来，供大家娱乐。

搜到这篇的小朋友们要继续加油哦 别怕,有我在~(气泡音

赛题

竞赛背景

心血管疾病 (CVD) 是全球第一大死因，估计每年夺走 $1790$万人的生命，占全球所有死亡人数的 $31\%$。五分之四的心血管疾病死亡是由心脏病发作和中风引起的，其中三分之一的死亡过早发生在 $70$ 岁以下的人群中。心力衰竭是由 CVD 引起的常见事件，该数据集包含 $11$ 个可用于分析可能的心脏病的特征。患有心血管疾病或处于高心血管风险（由于存在一种或多种风险因素，如高血压、糖尿病、高脂血症或已确诊的疾病）的人需要早期检测和管理。

字段说明

字段	解释
Age	患者年龄
性别	患者的性别[M：男，F：女]
ChestPainType	胸痛类型 [TA：典型心绞痛，ATA：非典型心绞痛，NAP：非心绞痛，ASY：无症状]
RestingBP	静息血压 [mm Hg]
Cholesterol	血清胆固醇 [mg/dl]
FastingBS	空腹血糖 [1：如果 FastingBS > 120 mg/dl，0：其它]
RestingECG	静息心电图结果 [正常：正常，ST：有 ST-T 波异常（T 波倒置和/或 ST 抬高或压低 > 0.05 mV），LVH：根据埃斯蒂斯标准显示可能或明确的左心室肥大]
MaxHR	达到的最大心率 [60 到 202 之间的数值]
ExerciseAngina	运动诱发的心绞痛 [Y：是，N：否]
Oldpeak	oldpeak = ST [在抑郁症中测量的数值]
ST_Slope	运动 ST 段的坡度[Up：向上倾斜，Flat：平坦，Down：向下倾斜]
HeartDisease	输出类[1：心脏病，0：正常]

考核目标

1. 数据的预处理;
2. 数据的可视化;
3. 分析可能导致心脏病的原因，并提出合理建议。

任务

根据所给的数据集“A 题.csv”提取码qwer， 完成以下任务：

任务一 数据预处理

1. 将 CSV 文件的数据先按照 Age 进行排序，然后取出前100 条数据，并命名为“task1_1.csv”保存在结果文件夹中；
2. 针对取出的前 100 条数据，统计出每个年龄的HeartDisease 为 1 的条数；
3. 统计出患有心脏病的人群中，各类型 ChestPainType 所占的比例，并写成百分比的格式以及四舍五入保留两位小数

任务二 数据可视化

1. 采用合适的可视化方法展示 HeartDisease 与 Age 之间的关系
2. 采用合适的可视化方法展示对于 HeartDisease 取不同值，RestingBP 和 Cholesterol 的
   大小关系
3. 采用合适的可视化方法展示 Sex 和 Cholesterol 对 HeartDisease 人数的影响

任务三 数据分析

1. 选取适当的方法分析哪些指标的异常会导致心脏病
2. 针对可能导致心脏病的指标，提出预防心脏病的合理建议

任务一思路

老三样，首先是一些基本的文件操作。

数据集共计12个变量，918个观测。为了方便用图形、表格展示处理结果，统计缺失值空值，绘制数据柱状图如下：

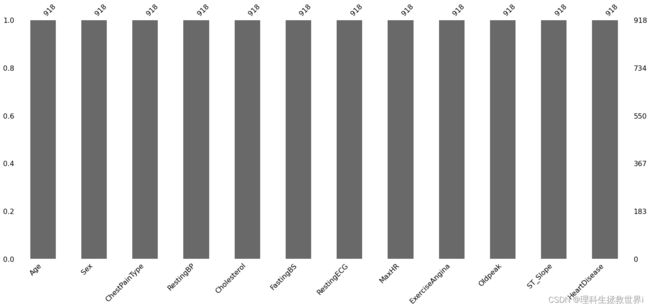
可以看出数据完整；根据字段说明寻找异常值这一步同样没有操作空间。注意到大多数变量为字符型变量，如果在这里就直接数值化交一套描述性统计分析只能说是比较幽默的。所以属于是一整个明牌的状态给到，上代码 :

import pandas as pd
df = pd.read_csv('A题.csv')
#1.1
df.sort_values(by='Age').head(100).to_csv('./result/task1_1.csv',encoding='utf_8_sig',index=False)
#1.2
data = pd.read_csv('./result/task1_1.csv')
data1_2 = data.loc[data['HeartDisease']==1]
data1_2.shape[0]#前100条HeartDisease为1的条数
data_group = data1_2.groupby('Age').agg({'HeartDisease':'sum'}) 
#1.3
data1_3=df.loc[df['HeartDisease']==1]
data1_3.shape[0]
nums = data1_3.groupby('ChestPainType').size()/data1_3.shape[0]
nums.map(lambda x: format(x, '.2%'))

熟悉pandas模块处理起来速度不输Excel的超级透视表。你忘了groupby语句也没有关系，只要思想不滑坡，这里安利一个超超级好用的pandas语句生成工具:D-Tale ，请使用jupyter nootbook以获得更佳的交互体验。

为了更好的展示结果，分别对1.2、1.3绘制条形图、环形图如下：

1.2

该样本中以38岁心脏病患者最多…

1.3

由于python自带的matplotlib模块画图稳定且一般…pyecharts提供了echarts图表接口，丰富的模板示例。需要注意0.版本和1.版本的pyecharts代码风格完全不一致，以python3.8为例，此处使用的就是pyecharts1.9.0版本。

pip install pyecharts==1.9.0

其中输入的数据的类型非常严格，以条形图x轴为例，必须由列表传入数据，且列表元素类型必须为字符串。

不同的图表携带的信息不相同，不同颜色所代表的信息也不同。比如环形图就较饼图有更好展示比例的效果；红色相较蓝色更显得?危险。因此对于任务二来说选取合适的图表很重要。

任务二思路

2.1

展示两个变量间的关系，散点图无疑是最好的选择。但对于 HeartDisease二值变量来说，散点往往会连成线。所以，此处使用红色表示HeartDisease=1，使用蓝色表示HeartDisease=0，重点研究患病人群，绘制堆叠条形图如下：

好起来了，有点中心极限定理那味了吧。

2.2

然后2.2就有点那个法网恢恢但是咱们另辟蹊径逃之夭夭，咱也进行了一个头脑风暴，既然，二维已经不能满足需求，那就是一个论文中不常见也不推荐的3D散点图给到，毕竟这一个图可以进行三个维度的产出，理论上携带的信息会更多 (可以编的更多) :

切记一切以论文输出为重点，选择自己熟悉，好说明的图形放在论文里，这里同样可以以HeartDisease为维数，绘制成两张散点图进行分析。切忌本末倒置。

2.3

最单纯，咱想看Sex和Cholesterol对HeartDisease人数的影响，趋势嘛，画多折线图：

这…是啥也看不出来，反倒是奇怪的血清胆固醇含量(Cholesterol)增加了。别怕 有我在~ 这个时候反而走了一条弯路：注意到不同性别是否患病四个样本的规模并不一致，如果画在同一张图，数据量较少，不存在的血清胆固醇含量一律用None值替代的话，pyecharts可能就会画出原本并不存在的折线(平滑过渡效果的弊端)，从而影响分析结果。以HeartDisease区分，当即绘制大聪明双条形图如下：

坏了，效果稍显一丢，但同样劝退吹水(震)…

这件事告诉我们无论如何画图效果都不好的情况下，请一定要找个中数据的原因。不要拘泥于字段说明，哪怕他什么都没说，时至今日也没有血清胆固醇为0，还活着的人！！！ 但是作为一个平时对心脏病毫无研究的无辜大学生，就算去除了异常值，x轴的长度同样是令人费解的，以医学上的分段(高中低)来展示Cholesterol 对 HeartDisease 人数这个方面的影响，图形精简，同时会损失一部分信息…所以就需要尽可能的发挥大家的想象力啦~

任务三思路

3.1

题目有意思的是要选取合适的方法，好嘛，文字游戏。单纯建立模型去写个人感觉并不好彩，所以3.1依然先走可视化的路线：
来啊 一发变量关系图甩过去：

似乎并不能发现什么很明显的关系…

接下来使用sklearn中LabelEncoder()，将标签变量数值化，并绘制各变量的密度曲线+直方图(这一步是做着玩的，可以更清楚的看到各个变量的分布情况)比如：

为了研究哪些指标的异常会导致心脏病，首先研究哪些指标和心脏病有关。针对心脏病患者，绘制不同变量下的折线图，通过患者人数判断何处为指标异常点，举栗：

心脏病患者在抑郁症中测量的各个数值(Oldpeak)人数如图，可以看出-0.6到0.1之间的患者数量最多。

心脏病患者运动 ST 段的各坡度(ST_Slope)人数如图，绝大多数人平时选择1，即平坦的路段进行运动，可以作为该项指标的异常…

3.2

为了减少后续小作文的压力，给建模方面一定的人文关怀，还是决定上个模型。这里选择了一个较为曲折、效果最差的老朋友：主成分！因为数据变量太多，变量可能存在一定的相关性，欲使其线性组合进行说明。

首先画一个相关系数热力图：

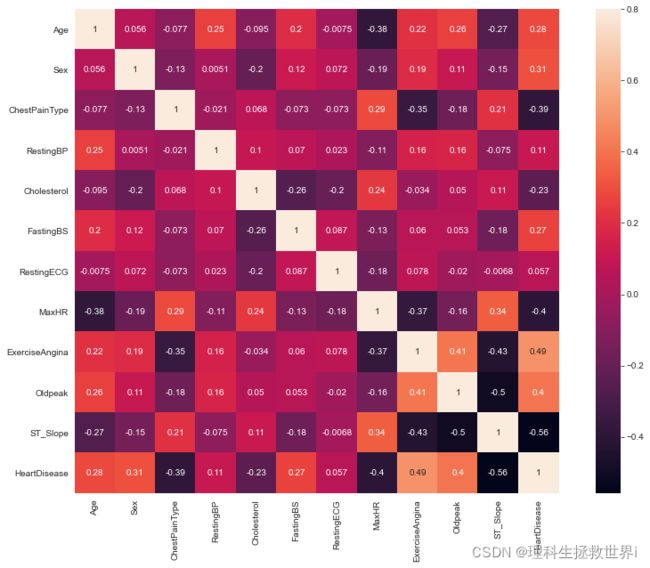
很好，变量间的相关性并不高。但我们不知道为什么还是想用主成分，ok，不忘初心，手写一个基于方差阵提取主成分走起：

##基于方差阵的主成分分析
#对数据进行标准化和归一化
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
ss = StandardScaler()
mm = MinMaxScaler()
data = ss.fit_transform(data.iloc[:,0:11])#数据
data = mm.fit_transform(data)
##正向化处理 默认数值越大越有可能患病
data1 = np.matrix(data)#11个特征
meanvals = np.mean(data1,axis=0)#计算每一列均值
meanremoved=data1-meanvals#归一化 减去均值
covmat = np.cov(meanremoved.T)#计算协方差矩阵 T转置 每一行代表一个变量（属性）
eigvals,eigvects=np.linalg.eig(np.mat(covmat))#计算矩阵特征值 特征向量
eigvects_lis = list(zip(eigvals,eigvects))
sortarray=np.sort(eigvals) #对特征值按照从小到大排序
sortarray=sortarray[-1::-1] #特征值从大到小排序  

arraysum=sum(eigvals) #数据集的方差和 

arrayshare = []#排序后特征值的方差贡献率  
for i in sortarray:
    arrayshare.append(i/arraysum)
 
percentage = 0.90#最小累计方差贡献率
tempsum=0
k=0
for i in sortarray:
    tempsum+=i
    k+=1
    if tempsum>=arraysum*percentage:
        break
print('大到小排序的特征值：',sortarray)
print('各个特征值的贡献率:',arrayshare)
print('累计贡献率超过0.85的特征个数:',k)#此处k为6，即85%的信息可由这6个特征表示

eigvalind = sortarray[:k:1]#获取7个特征值
redeigvects = np.zeros(shape=(7,11))#8
for key,i in enumerate(eigvalind):
    for j in eigvects_lis:
        if i==j[0]:
            redeigvects[key] = np.array(j[1]) 

print('特征值：',eigvalind)
print('特征值对应的特征向量：',redeigvects)
print('综合评价模型权重：',arrayshare[0:k])#综合评价模型

不出所料，吹水的同学还是得继续扛米，6个主成分的解释向来也是个想象力环节，至于综合评价模型也需要根据主成分的系数，也就是贡献率进一步说明…emm 这向来不是我的活，或许以后更新算法内容时再进一步说明， 此处便不做赘述。

总结

算是一个新手一般友好的题，数据量上并没有要求，着重可视化和论文能力。至于标签变量的处理相对有难度。不要局限于已有的模型，总归是有合适的，为什么不能是树状模型呢？

最后 大家可以去b站关注一下嘉然今天吃什么吗？