时间序列模型算法 - ARIMA （一）

1.时间序列模型概述

时间序列是研究数据随时间变化而变化的一种算法。是一种预测性分析算法。它的基本出发点就是事物发展都有连续性，按照它本身固有的规律进行。

时间序列的常用算法包括：

有这几个那如何选择模型呢

首先我们要知道时间序列就是按照时间顺序排列，随时间变化的随机过程，也就是说有对应的均值、方差、协方差等。
时间序列可以解决在只有时间（序列项）而没有其他可控变量下对未来数据的预测问题，常用于经济预测、股市预测、天气预测等。

如果随机过程随着时间变化，则此过程是非平稳的，相反，如果随机过程的特征不随时间变化，则此过程为平稳的

• 如果导致非平稳的原因确定：ES、MA、AR、ARMA
• 如果是平稳序列：ARIMA

1.1 时间序列的不同分类

时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序列的方法构成数据分析的一个重要领域，即时间序列分析。

时间序列根据研究的依据不同，可有不同的分类。

1. 按研究对象的多少划分，有一元时间序列和多元时间序列。
2. 按时间的连续性将时间序列分为离散时间序列和连续时间序列两种。
3. 按序列的统计特性划分，有平稳时间序列和非平稳时间序列。

如果一个时间序列的概率分布与时间t无关，则称该序列为严格的（狭义）平稳时间序列。

如果序列的一、二阶矩存在，而且对任意时刻t满足：

（1）均值为常数

（2）协方差为时间间隔 T 的函数。则称为宽平稳（广义）时间序列。以后研究的时间序列主要是宽平稳时间序列。

4. 按时间序列的分布规律划分，有高斯型时间序列和非高斯型时间序列。

1.2 确定性时间序列分析方法概述

一个时间序列可以分解为以下四部分：

（1）长期趋势变动。它指时间序列朝一定方向持续上升或下降，或停留在某一水平上，它反映了客观事物的主要变化趋势。

（2）季节变动。

（3）循环变动。通常指周期为一年以上，由非季节因素引起的波形相似的波动。

（4）不规则变动。通常为突然变动和随机变动。

1.3 三种时间序列模型

通常用$T_t$ 表示长期趋势项，$S_t$ 表示季节变动趋势项，$C_t$ 表示循环变动趋势项，$R_t$ 表示随机干扰项。常见的确定性时间序列模型有以下类型：

（1）加法模型

$y_t=T_t+S_t+C_t+R_t$

（2）乘法模型

$y_t=T_t\ast S_t\ast C_t\ast R_t$

（3）混合模型

$y_t=T_t\ast S_t+R_t$

$y_t=S_t+T_t\ast C_t\ast R_t$

其中 $y_t$ 是观测目标的观测记录，$E(R_t)=0$， $E(R_t^2)={\sigma }^2$。

2.指标平滑ES

2.1 一次指数平滑法

线性回归算法中，每个经验点的权重是一致的，即很早以前的经验数据也可能对预测数据有较大的影响。很多实际场景中，未来一段时间的趋势可能和在最近一段时间的趋势关系更加紧密。比如小明去年数学考试成绩一直不及格，今年连续多次考试90多分，预测小明下一次数学考试的成绩，情理上90多分的可能性更高。采用传统的线性回归算法，预测结果可能是70多分。

指数平滑法原则认为，时间越靠过去的经验数据对趋势的影响越小。我们假定时间t的观测值为y(t)，时间t的预测值为S(t)，则时间t+1的预测值S(t+1)为
$$S_{t+1}=a{y}_t+(1-a)S_t$$
a的取值范围在(0,1)，a越大，最近时间点的观测值对预测值的影响越大

另外还有二次指数平滑、三次指数平滑，就不介绍，懒得写

3.ACF与PACF

首先来说ACF与PACF是用来确定模型AR(p,)、MA(q,)、ARMA(p,q)、ARIMA(p,l,q)，中p、q。方法如下：

• 截尾：落在置信区间（95%的点都符合该规则）

如何用PACF图和ACF图来确定p、q值
通常我们确定了模型后，看模型的数据的阶数和2倍标准差范围。

这里先解释一下 阶数就是历史观测项，比如当前时间t数据为$x_t$阶数为7，表示$x_{t-7}$。

开始可以对照上面的表进行分析

acf、pacf图如下图

可以看到acf图中q到7阶段时，后续的值逐渐倾向于0的，是符合拖尾的，在pacf图中p到1阶段时，后续的值逐渐倾向于0的。所以模型为AR(1)，

假设选择模型为ARMA

其acf、pacf图如下图

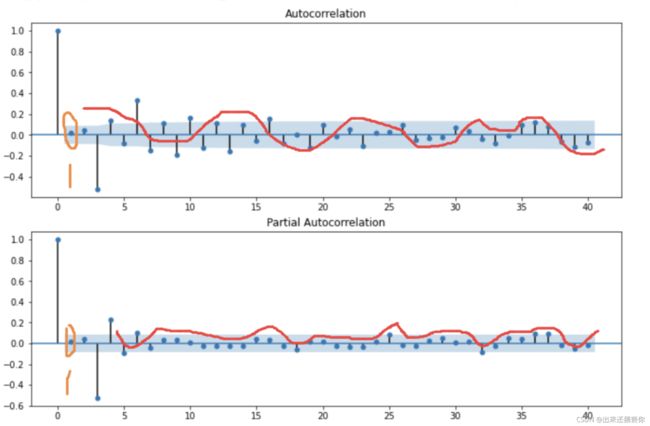
ACF和PACF都呈现衰减趋于零，在1阶位置就开始基本落在2倍标准差范围，所以是ARMA(1,1)模型

4.AR

AR是线性时间序列分析模型，通过自身当前数据与历史之前的数据之间的相关关系(自相关)来建立回归方程，
在时间序列中，当前观测值可以通过历史的观测值，结合相关性获得，公式如下：

$$Y_t=c+{\Phi }_1{Y}_{t-1}+{\Phi }_2{Y}_{t-2}+......+{\Phi }_p{Y}_{t-p}+{\xi }_t$$

公式中${\xi }_t$为噪声，$Y_{t-1}$,$Y_{t-2}$是历史观测项，$p$是历史观测值

5.MA

过将一段时间序列中白噪声序列进行加权和，可以得到移动平均方程。
在时间序列中，当前观测值是由历史的误差的线性组合成的，这些误差互相独立分布且服从正态分布。公式如下：
$$Y_t=c+{\xi }_t+{\theta }_1{\xi }_{t-1}+{\theta }_2{\xi }_{t-2}+......+{\theta }_q{\xi }_{t-q}$$

6.ARMA

自回归移动平均模型是与自回归和移动平均模型两部分组成。
ARMA(p,q)模型全称为自回归移动平均模型，公式如下：
$$Y_t=c+{\Phi }_1{Y}_{t-1}+{\Phi }_2{Y}_{t-2}+......+{\Phi }_p{Y}_{t-p}+{\xi }_t+{\theta }_1{\xi }_{t-1}+{\theta }_2{\xi }_{t-2}+......+{\theta }_q{\xi }_{t-q}$$

7.ARIMA

ARIMA(p,d,q)模型全称为差分自回归移动平均模型
(Autoregressive Integrated Moving Average Model,简记ARIMA).
自回归(AR),差分(I),移动平均（MA）
趋势参数：

• p：趋势自回归阶数。
• d：趋势差分阶数。
• q：趋势移动平均阶数。

ARIMA与ARMA模型公式都是一样的，区别在于，ARIMA公式中的Y变成差分算子(即Y是经过原始Y值差分计算了一次的新值)，保证了数据 的稳定性。

7.1 差分

差分（difference）又名差分函数或差分运算，差分的结果反映了离散量之间的一种变化，是研究离散数学的一种工具。它将原函数f(x) 映射到f(x+a)-f(x+b) 。差分运算，相应于微分运算，是微积分中重要的一个概念。总而言之，差分对应离散，微分对应连续。差分又分为前向差分、向后差分及中心差分三种。

通常情况下我们用到的是前向差分公式如下：

$$x_k=x_0+kh,(k=0,1,...,n)$$
$$△f(x_k)=f(x_{k+1})-f(x_k)$$

差分的阶

称为阶的差分，即前向阶差分 ，如果数学运用根据数学归纳法，有其中，为二项式系数。特别的，有前向差分有时候也称作数列的二项式变换

以物理学中来理解，一个汽车位移与时间的问题。

一阶导数表示速度，二阶差分表示速度的导数加速度。同样的，在时间序列模型中，一阶差分表示相邻时间的数据的变化情况，二阶差分就表示这种变化的变化强弱。

8. ARIMA实践

8.1 读取数据

这里的数据集AirPassengers.csv，百度都搜到得

import numpy as np
import pandas as pd
from datetime import datetime
import matplotlib.pylab as plt
data=pd.read_csv('AirPassengers.csv',encoding='utf-8')
data.head(5)

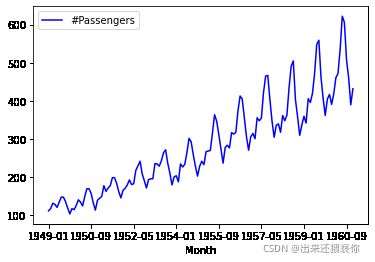
8.2 画图，观察数据是否非平稳

def draw_ts(timeSeries):
    f = plt.figure(facecolor='white')
    timeSeries.plot(color='blue')
    plt.legend()
    plt.show()
draw_ts(data)

从图中看，序列是非平稳时间序列。

8.3 差分，观察数据

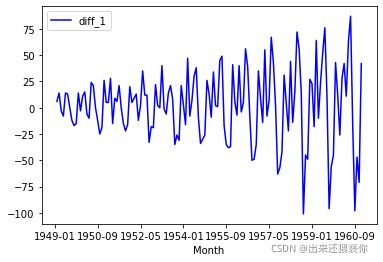
一阶差分

data['diff_1']=data.diff()
draw_ts(data['diff_1'])

二阶差分，我们通常最多就做到二阶差分就行

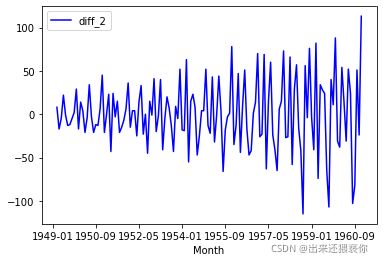
data['diff_2']=data['diff_1'].diff()
draw_ts(data['diff_2'])

大致可以看图，差分为平稳时间序列

8.4 单位根检验，确定数据为平稳时间序列

单位根检验背后的直觉是它确定趋势定义时间序列的强度。

有许多单位根测试，Augmented Dickey-Fuller可能是更广泛使用的之一。它使用自回归模型并优化跨多个不同滞后值的信息标准。

测试的零假设是时间序列可以用单位根表示，它不是静止的（具有一些时间依赖的结构）。替代假设（拒绝零假设）是时间序列是静止的。

• 空假设（H0）：如果未被拒绝，则表明时间序列具有单位根，这意味着它是非平稳的。它有一些时间依赖的结构。
• 替代假设（H1）：零假设被拒绝;
  它表明时间序列没有单位根，这意味着它是静止的。它没有时间依赖的结构。

我们使用测试中的p值来解释这个结果。在下面的代码反馈结果也会出现p。低于阈值的p值（例如5％或1％）表明我们拒绝零假设（静止），否则高于阈值的p值表明我们未能拒绝零假设（非静止）。

• p值> 0.05：无法拒绝原假设（H0），数据具有单位根并且是非平稳的。
• p值<=0.05：拒绝原假设（H0），数据没有单位根并且是静止的。

我们先用原数据进行检验看看。

def testStationarity(ts):
    dftest = adfuller(ts)
    # 对上述函数求得的值进行语义描述
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
    for key,value in dftest[4].items():
        dfoutput['Critical Value (%s)'%key] = value
    return dfoutput
testStationarity(data)

上图我们只需关注p值，其余的参数解释如下：

• Test Statistic：ADF检验的结果
• p-value：p值
• Lags Used：滞后数量
• Number of Observations Used：用于ADF回归和临界值计算的数量
• Critical Value：临界值1%、5%、10%

下面我们用1阶差分来检验

diff_1=data.diff()
diff_1 = diff_1.dropna()
testStationarity(diff_1)

从结果来看还无法拒绝原假设（原假设为是平稳时间序列），这时候我们通常对原数据先进行对数处理，再进行一次差分。

del data['diff_1']
del data['diff_2']
ts_log = np.log(data)
draw_ts(ts_log)

logdiff_1=ts_log.diff(12)
logdiff_1 = logdiff_1.dropna()
logdiff_2=logdiff_1.diff(1)
logdiff_2=logdiff_2.dropna()
testStationarity(logdiff_2)

p值小于0.05，拒绝原假设（原假设为是平稳时间序列），故数据为平稳时间序列

8.5 Q检验，检验是否数据具有相关性

检验当前时刻t到滞后时刻k(Lags Used)，$y_t$与y_{t-k}的相关性。
由上小节得到的滞后值为12.

from statsmodels.stats.diagnostic import acorr_ljungbox
acorr=acorr_ljungbox(logdiff_2,lags=12)
acorr

这里acorr[0]为这12个时刻的统计值，acorr[1]，为t时刻的统计值与滞后的12时刻的相关性。
从结果可以看出，p值较小，拒绝原假设（没有相关性），故数据有序列相关性

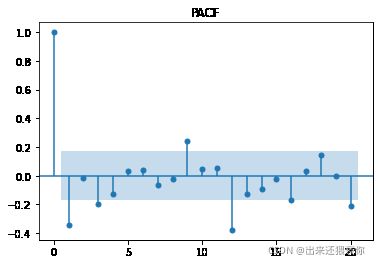
8.6 确定AR和MA，画ACF、PACF判断

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
pacf = plot_pacf(logdiff_2, lags=20)
plt.title('PACF')
pacf.show()

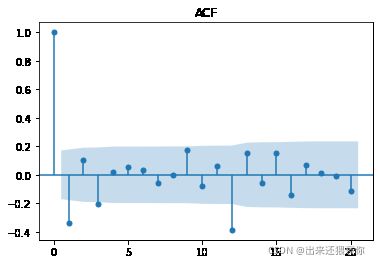
acf = plot_acf(logdiff_2, lags=20)
plt.title('ACF')
acf.show()

从图可得 p=1，q=1

8.7 使用AIC、BIC最小准则确定p、q

import statsmodels.tsa.stattools as st
model = st.arma_order_select_ic(logdiff_2, max_ar=5, max_ma=5, ic=['aic', 'bic', 'hqic'])
model.bic_min_order 

返回（2，3）

8.8 拟合ARIMA或者ARMA模型

使用差分后的数据

from statsmodels.tsa.arima_model import ARMA
model_arma = ARMA(logdiff_2, order = model.bic_min_order)
result_arma = model_arma.fit(disp = -1, method = 'css')

使用原始数据

from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(data, order=(1,1,1))
result = model.fit()

8.9 检验模型效果：残差检验

残差检验，对已经训练好的模型，对模型的残差，进行可视化，
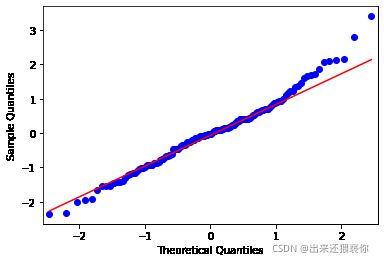
对残差进行可视化，判断残差是否符合正态分布

• 若为正态分布则恭喜你，模型建立完毕
• 若不为正态分布，则说明残差中还有有用信息，需要你优化模型啦

resid = result.resid
from statsmodels.graphics.api import qqplot
qqplot(resid, line='q', fit=True)
plt.show()

8.10 预测

pred = result.predict(start=1, end =len(data) + 10 ) # 从训练集第0个开始预测(start=1表示从第0个开始)，预测完整个训练集后，还需要向后预测10个
print(len(pred))
print(pred[-10:]) # 有负数，表明是一阶差分之后的
# 此时可以画出预测的曲线和data_diff进行比较

8.11 将预测的平稳值还原为非平稳序列

result_fina = np.array(pred[0:-10]) + (np.array(data.shift(1)))
result_fina

# 如果还取了对数，进行如下操作
# result_log_rev = np.exp(result_fina)
# result_log_rev.dropna(inplace=True)