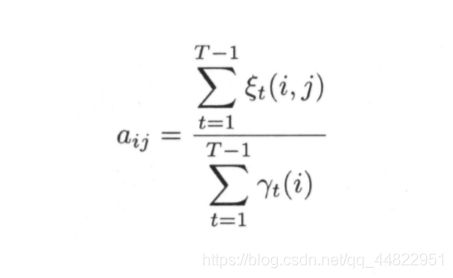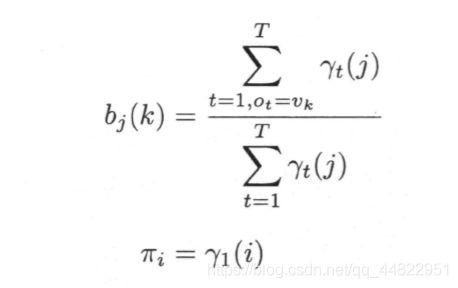统计学习方法笔记-隐马尔可夫模型（内含Python代码实现)
一 马尔可夫模型
我们通过一个具体的例子来介绍一下什么是马尔可夫模型
我们假设天气有3种情况，阴天，雨天，晴天，它们之间的转换关系如下:
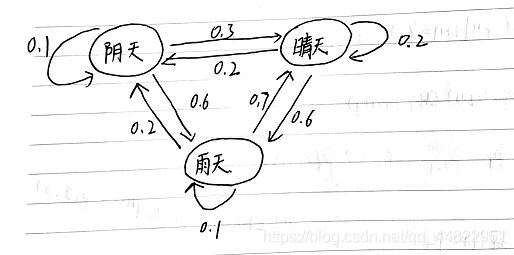(稍微解释一下这个图，我们可以这样认为，已知第一天是阴天，那第二天是阴天的概率是0.1， 第二天是晴天的概率是0.3，第二天是雨天的概率是0.6)
每一个状态转换到另一个状态或者自身的状态都有一定的概率。
马尔可夫模型就是用来表述上述问题的一个模型。
有这样一个状态链，第一天是阴天，第二天是晴天，第三天是雨天。 这样一个状态链就是马尔可夫链。
在上述例子中，如果我们并不知道今天天气属于什么状况，我们只知道今明后三天的水藻的干燥湿润状态，因为水藻的状态与天气有关，我们用水藻状态来推测出这三天的天气，就需要用到隐马尔科夫模型。
下面我们将介绍一下隐马尔可夫模型
二 隐马尔可夫模型
隐马尔可夫模型定义
隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列， 再由各个状态生成一个观测从而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列，称为状态序列 ;每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列。序列的每一个位置又可以看作是一个时刻。
隐马尔可夫模型的组成
(这一块看的比较懵没关系，下面会结合例子解释哦)
设 Q是所有可能的状态集合 Q ={q1,q2,…qN} V是所有可能的观测的集合 V={v1,v2,…vM}
N是可能的状态数，M是可能的观测数
I 是长度为T的状态序列 I={i1,i2,…iT}
O 是状态序列对应的观测序列 O={o1,o2,…oT}
隐马尔可夫模型由以下三部分组成
1 初始状态概率向量 π
π=（πi)
其中 πi=P(i1 = qi) 表示在时刻 t=1 处于状态qi的概率
2 状态转移概率矩阵 A
A=[aij] N*N
其中aij = P( it+1 = qj | it = qi) 表示在t时刻处于状态qi 的情况下在t+1时刻转移到状态qj 的概率。
3 观测概率矩阵 B
B = [ bj(k) ] N*M
bj(k) = P(ot = vk| it = qj) 表示在时刻 t 处于状态qj 的条件下生成观测vk 的概率。
隐马尔可夫模型一般表示为
我们来看一个具体的例子体会一下这些符号都是什么意思
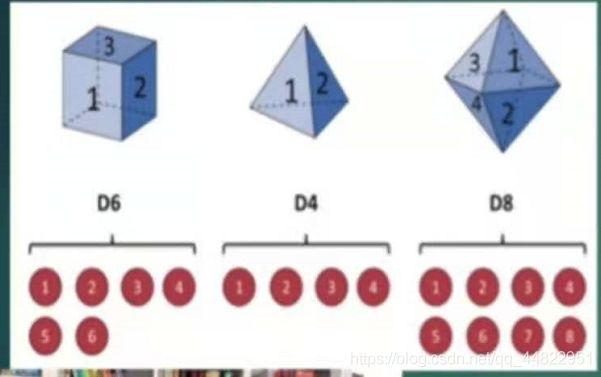
我们有三种骰子 分别是六面体骰子（它的值为1，2，3，4，5，6） 四面体骰子(它的值为1，2，3，4) 八面体骰子 (它的值为1，2，3，4，5，6，7，8) 把这三种骰子放到一个盒子中 有放回的去抽一个骰子，拿到这个骰子之后，抛起这个骰子记录它的数字。重复这个动作多次，得到一个数字序列。
假设我们做了10次这个动作 得到的序列为 1，6，3，5，2，7，3，5，2，4
假设状态转换图是这样的
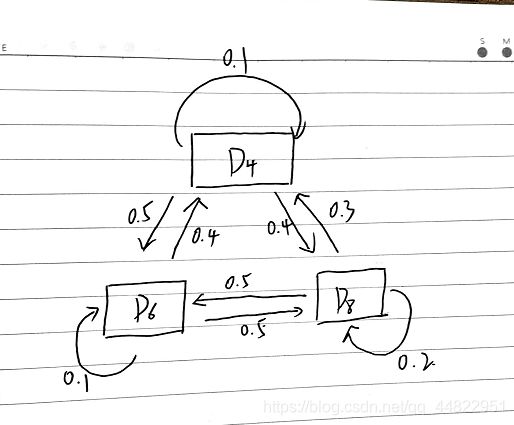(解释一下: 假如某一次的骰子是D4 那下一次抽到的骰子是D4的概率是0.1 ，下一次抽到的骰子是D8的概率是 0.4 下一次抽到的骰子是D6 的概率是0.5.）
题目介绍完了，我们来分析一下
在本例中，我们的状态就是不同种类的骰子
所以 Q={D4,D6,D8} N=3
我们的观测集合就是骰子上的数字可能的情况
V={1,2,3,4,5,6,7,8} M=8
我们的观测序列是 多次掷骰子得到的一个数字序列 1，6，3，5，2，7，3，5，2，4
初始时刻 我们从盒子里选择一个骰子，因为是随机选择，抽到每一个骰子的概率都是 1/3.
则初始状态向量 π =（1/3，1/3，1/3）
状态转移概率矩阵 A (根据上方给出的状态转换图得到)
观测概率矩阵 B (在某一状态下，生成某一观测的概率)
隐马尔可夫模型的两个假设
齐次马尔可夫性假设，即假设隐藏的马尔可夫链在任意时刻 t 的状态只依赖于其前一时刻的状态
观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态
隐马尔可夫模型有三个需要解决的问题分别是概率计算问题，学习问题，预测问题。在下文将一 一 介绍。
三 概率计算问题
概率计算问题指的是给定一个隐马尔可夫模型 λ =（A,B,π) ,和观测序列O = (o1， o2， … ， oT), 在模型 λ 下观测序列O 出现的概率P(OIλ)。
直接计算法
这是一种理论上可行，但是由于计算量太大，导致计算上不可行的方法，了解即可。
前向算法
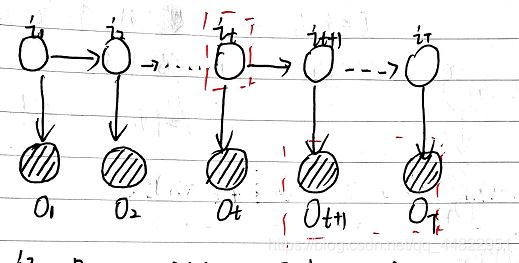
先介绍一个概念: 前向概率
给定隐马尔可夫模型 λ，定义到时刻 t 部分观测序列为 o1， o2， … ， ot 且状态为 qi 的概率为前向概率，记作 αt(i) = P(o1,o2,…,ot, it=qi| λ)
前向算法可以递推地求得前向概率αt(i) 从而得到观测序列概率 P(OIλ)。
观测序列概率的前向算法如下:
前向算法的一些推导
前向算法计算例子
后向算法
后向概率
给定隐马尔可夫模型 λ，定义在时刻 t 状态为 qi 的条件下，从 t+1 到 T 的部分观测序列为 Ot+1， Ot+2， … ， OT的概率为后向概率，记作βt(i) = P(Ot+1, Ot+2 ,…,OT| it = qi， λ)
观测序列概率的后向算法
后向算法相关推导
利用前向概率和后向概率的定义可以将观测序列概率 P(OIλ) 统一写成
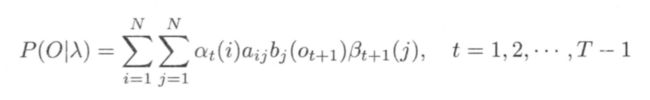我们可以根据前向概率和后向概率来表示一些概率和期望值的计算。
根据以上则
在观测O下状态 i 出现的期望值:
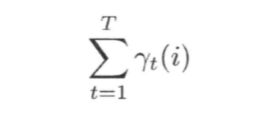在观测 O 下由状态 i 转移的期望值:
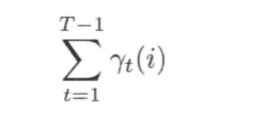在观测O下由状态 i 转移到状态 j 的期望值:
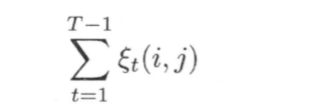
四 隐马尔可夫模型的学习问题
假设给定训练数据只包含 S 个长度为 T 的观测序列 {O1，O2，…， Os} 而没有对应的状态序列，隐马尔可夫模型的学习问题的目标是学习隐马尔可夫模型 λ = (A， B， π )的参数。我们将观测序列数据看作观测数据 O，状态序列数据看作不可观测的隐数据 I，那么隐马尔可夫模型事实上是一个含有隐变量的概率模型.
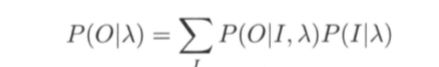它的参数学习可以由 EM 算法实现，该算法命名为Baum-Welch.
下面给出用EM算法求解隐马尔可夫模型参数的详细推导
参数估计为
五 隐马尔可夫模型的预测问题
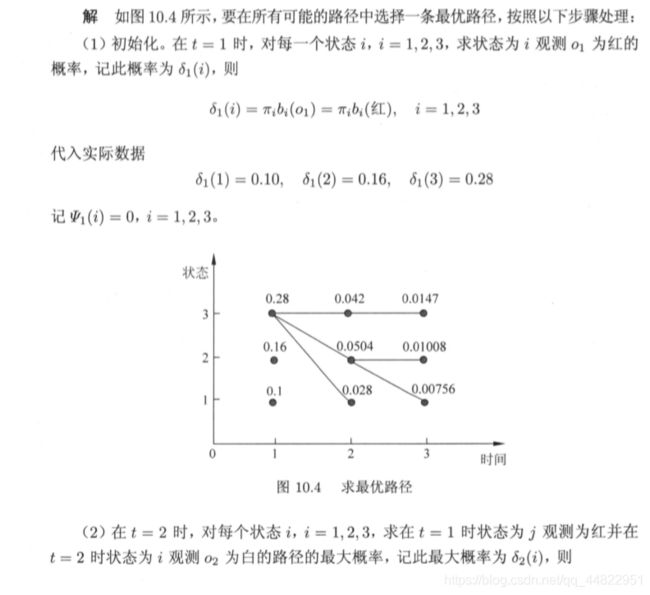
隐马尔可夫模型的预测问题，也称为解码问题。已知模型 λ = (A， B， π ) 和观测序列O=(o1,o2,…oT),求对给定观测序列条件概率P(I |O) 最大的状态序列I=(i1,i2,…iT). 即给定观测序列，求最有可能的对应的状态序列。
我们用的方法是维特比算法，下面介绍一下维特比算法。
维特比算法是一个基于动态规划思想的方法，它把求解状态序列看作寻找一条最优路径。
维特比算法是这样的
维特比算法示例
该示例代码实现如下
class Viterbi:
def __init__(self,o,A,B,PI,index):
self.o=o
self.A=A
self.B=B
self.index = index
self.N=self.A.shape[0] #状态集合有多少元素
self.M = len(self.index) # 观测集合有多少元素
self.T =len(self.o) #观测序列一共有多少值
self.PI=PI # 初始状态概率
self.delte=[[0]*self.N]*self.T
self.I=[] #得到的状态序列是
self.keci=[[0]*self.N]*self.T
def cal_delte(self):
# 在书中时刻t的取值是 1到 T 但是写代码数组是从0 开始的 方便起见 我们讲t也从0开始
o1=self.o[0]#第一个观测变量是
o1_index=self.index[o1] #第一个观测变量的下标是
for i in range(self.N):
self.delte[0][i] = self.PI[i]*self.B[i][o1_index]
for t in range(1,self.T):#从时刻t=1 开始 到T-1
ot=self.o[t]
ot_index=self.index[ot]
for i in range(self.N):
max=0
maxj=0
for j in range(self.N):
a = self.delte[t-1][j] *self.A[j][i]*self.B[i][ot_index]
if a>max:
max=a
maxj=j
self.delte[t][i]= max
self.keci[t][i]=maxj
def cal_max_path(self):
max=0
maxi=0
path=[]
for i in range(self.N):
a=self.delte[self.T-1][i]
if a>max:
max=a
maxi=i
path.append(maxi+1)
for t in range(self.T-1,0,-1):
maxi=self.keci[t][maxi]
path.append(maxi+1)
for i in range(len(path)-1,-1,-1):
self.I.append(path[i])
print(self.I)
A=np.array([[0.5,0.2,0.3],
[0.3,0.5,0.2],
[0.2,0.3,0.5]])
B=np.array([[0.5,0.5],
[0.4,0.6],
[0.7,0.3]])
PI=np.array([[0.2],
[0.4],
[0.4]])
o=['红','白','红']
index={'红':0,'白':1}
hmm=Viterbi(o,A,B,PI,index)
hmm.cal_delte()
hmm.cal_max_path()
六 隐马尔可夫模型代码实现
class HMM:
def __init__(self,o,status,observe,n):
self.o=o #观测数据
self.status= status #状态集合
self.observe=observe# 观测集合
self.N = len(self.status) # 状态集合有多少元素
self.M = len(observe) # 观测集合有多少元素
self.A = [[1 / self.N] * self.N] * self.N
self.B = [[1/self.M]*self.M]* self.N
self.T = len(self.o) # 观测序列一共有多少值
self.PI = [1/self.N]*self.N # 初始状态概率 N个状态 每个状态的概率是1/N
self.delte = [[0] * self.N] * self.T
self.I = [] # 得到的状态序列是
self.psi = [[0] * self.N] * self.T
self.a=self.cal_a()
self.b=self.cal_b()
self.n=n
def cal_a(self):
#计算前向概率
o1=self.o[0]
o1_index=self.observe[o1]
a=[[0]*self.N]*self.T
for i in range(self.N):
a[0][i]=self.PI[i]*self.B[i][o1_index]
for t in range(1, self.T): # 从时刻t=1 开始 到T-1
ot=self.o[t]
ot_index = self.observe[ot]
for i in range(self.N):
sum=0
for j in range(self.N):
sum += a[t-1][j]*self.A[j][i]
a[t][i]=sum*self.B[i][ot_index]
return a
def cal_b(self):
#计算后向概率
b = [[0] * self.N] * self.T
for i in range(self.N):
b[self.T-1][i] = 1
for t in range(self.T-2,-1,-1):
ot_add_1 = self.o[t+1]
ot_ot_add_1_index = self.observe[ot_add_1]
for i in range(self.N):
sum=0
for j in range(self.N):
sum+=self.A[i][j]*self.B[j][ot_ot_add_1_index]*b[t+1][j]
b[t][i]=sum
return b
def cal_gamma(self, t, i):
# 计算李航《统计学习方法》 p202 公式10.24
sum = 0
for j in range(self.N):
sum += self.a[t][j] * self.b[t][j]
# print(self.a)
# print(self.b)
return self.a[t][i] * self.b[t][i] / sum
def cal_xi(self, t, i1, j1):
# 计算李航《统计学习方法》 p203 公式10.26
sum = 0
ot_add_1 = self.o[t + 1]
ot_ot_add_1_index = self.observe[ot_add_1]
for i in range(self.N):
for j in range(self.N):
sum += self.a[t][i] * self.A[i][j] * self.B[j][ot_ot_add_1_index] * self.b[t + 1][j]
p = self.a[t][i1] * self.A[i1][j1] * self.B[j1][ot_ot_add_1_index] * self.b[t + 1][j1]
return p / sum
def update_A(self):
for i in range(self.N):
for j in range(self.N):
sum1=0
sum2=0
for t in range(self.T - 1):
sum1+=self.cal_xi(t,i,j)
sum2+=self.cal_gamma(t,i)
self.A[i][j]=sum1/sum2
def update_B(self):
for j in range(self.N):
for k in range(self.M):
sum1=0
sum2=0
for t in range(self.T):
ot=self.o[t]
ot_index=self.observe[ot]
if ot_index == k:
sum1+=self.cal_gamma(t,j)
sum2+=self.cal_gamma(t,j)
self.B[j][k]=sum1/sum2
def update_pi(self):
for i in range(self.N):
self.PI[i]=self.cal_gamma(0,i)
def fit(self):
for i in range(self.n):
print(i)
self.update_A()
self.update_B()
self.update_pi()
self.a = self.cal_a()
self.b = self.cal_b()
def cal_delte(self):
# 在书中时刻t的取值是 1到 T 但是写代码数组是从0 开始的 方便起见 我们讲t也从0开始
o1=self.o[0]#第一个观测变量是
o1_index=self.observe[o1] #第一个观测变量的下标是
for i in range(self.N):
self.delte[0][i] = self.PI[i]*self.B[i][o1_index]
for t in range(1,self.T):#从时刻t=1 开始 到T-1
ot=self.o[t]
ot_index=self.observe[ot]
for i in range(self.N):
max=0
maxj=0
for j in range(self.N):
a = self.delte[t-1][j] *self.A[j][i]*self.B[i][ot_index]
if a>max:
max=a
maxj=j
self.delte[t][i]= max
self.psi[t][i]=maxj
def cal_max_path(self):
max=0
maxi=0
path=[]
for i in range(self.N):
a=self.delte[self.T-1][i]
if a>max:
max=a
maxi=i
path.append(maxi+1)
for t in range(self.T-1,0,-1):
maxi=self.psi[t][maxi]
path.append(maxi+1)
for i in range(len(path)-1,-1,-1):
self.I.append(path[i])
print(self.I)
o=['红','白','红']
observe={'红':0,'白':1}
status=[1,2,3]
hmm=HMM(o,status,observe,200)
hmm.fit()
hmm.cal_delte()
hmm.cal_max_path()
参考
李航《统计学习方法》
b站视频 机器学习-白板推导系列(十四)-隐马尔可夫模型HMM