菜菜的sklearn-01决策树完整版
菜菜的sklearn-01决策树完整版
文章目录
- 菜菜的sklearn-01决策树完整版
- 一、决策树工作原理
-
- 模块sklearn.tree
- sklearn的基本建模流程
- 二、DecisionTreeClassifier--分类树
-
- 2.1 重要参数
-
- 2.1.1 criterion 不纯度参数
-
- 使用实例来理解不纯度
- 2.1.2 random_state & splitter
-
- 补充graphviz生成的tree.dot怎么变成graphviz以及中文乱码问题:
- 2.1.3 剪枝参数
-
- 2.1.3.1 max_depth --限制树的最大深度
- 2.1.3.2 min_samples_leaf --限制节点后的子节点
- 2.1.3.3 max_features & min_impurity_decrease --限制特征个数
- 2.1.4 使用超参数的学习曲线和网格搜索技术确认最优剪枝参数
-
- 2.1.4.1 超参数学习曲线
- 2.1.4.2 网格搜索技术
- 2.2 重要属性和接口
- 三、DecisionTreeRegressor--回归树
-
- 3.1 重要参数、属性和接口
-
- 3.1.1 criterion--回归树衡量分枝质量的指标
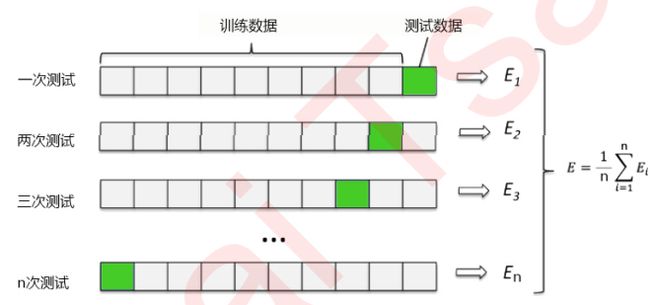
- 3.1.2 交叉验证
- 3.2 用回归树拟合正弦曲线实例
-
- 3.2.1 一维回归的图像绘制
- 3.2.2 kaggle泰坦尼克号幸存者的预测
- 3.3 网格搜索技术
- 3.3 网格搜索技术
本文章是基于bilibili菜菜的机器学习完成的,文字内容可能不全,主要是代码全以及代码讲解。方便我自己看!
一、决策树工作原理
决策树(Decision Tree)是一种非参数的有监督学习方法,它能够从一系列有特征和标签的数据中总结出决策规 则,并用树状图的结构来呈现这些规则,以解决分类和回归问题。
决策树算法的核心是要解决两个问题:
- 如何从数据表中找出最佳节点和最佳分枝?
- 如何让决策树停止生长,防止过拟合?
几乎所有决策树有关的模型调整方法,都围绕这两个问题展开。
模块sklearn.tree
sklearn中决策树的类都在”tree“这个模块之下。这个模块总共包含五个类:
| tree.DecisionTreeClassifier | 分类树 |
|---|---|
| tree.DecisionTreeRegressor | 回归树 |
| tree.export_graphviz | 将生成的决策树导出为DOT格式,画图专用 |
| tree.ExtraTreeClassifier | 高随机版本的分类树 |
| tree.ExtraTreeRegressor | 高随机版本的回归树 |
本篇主要会用到前两个模块:分类树和回归树!
sklearn的基本建模流程
对应代码:
from sklearn import tree
clf = tree.DecisionTreeClassifier() #实例化
clf = clf.fit(x_train,y_train) #用训练集训练数据模型
result = clf.score(x_test,y_test) #导入测试集,从接口中调用需要的信息
二、DecisionTreeClassifier–分类树
class sklearn.tree.DecisionTreeClassifier (criterion=’gini’, splitter=’best’, max_depth=None,
min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None,
random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None,
class_weight=None, presort=False)
2.1 重要参数
2.1.1 criterion 不纯度参数
为了要将表格转化为一棵树,决策树需要找出最佳节点和最佳的分枝方法,对分类树来说,衡量这个“最佳”的指标 叫做不纯度。
-
通常来说,不纯度越低,决策树对训练集的拟合越好。
-
现在使用的决策树算法在分枝方法上的核心大多是围绕在对某个不纯度相关指标的最优化上。
-
不纯度基于节点来计算,树中的每个节点都会有一个不纯度,并且子节点的不纯度一定是低于父节点的,也就是说在同一棵决策树上,叶子节点的不纯度一定是最低的。
-
LeTAX
-
Criterion这个参数正是用来决定不纯度的计算方法的。sklearn提供了两种选择:
-
criterion = “entropy”–使用信息熵(Entropy)
-
criterion = “gini”–使用基尼系数(Gini Impurity)
E n t r o p y ( t ) = − ∑ i = 0 c − 1 p ( i ∣ t ) l o g 2 p ( i ∣ t ) Entropy(t) = -\sum_{i=0}^{c-1}p(i|t)log_2p(i|t) Entropy(t)=−i=0∑c−1p(i∣t)log2p(i∣t)G i n i t = 1 − ∑ i = 0 c − 1 p ( i ∣ t ) 2 Ginit = 1-\sum_{i=0}^{c-1}p(i|t)^2 Ginit=1−i=0∑c−1p(i∣t)2
其中, p ( i ∣ t ) = p ( i t ) p ( t ) 代表 i 在 t 之下的条件概率 其中,p(i|t)=\frac{p(it)}{p(t)}代表i在t之下的条件概率 其中,p(i∣t)=p(t)p(it)代表i在t之下的条件概率
其中t代表给定的节点,i代表标签的任意分类, p ( i ∣ t ) p(i|t) p(i∣t)代表标签分类i在节点t上所占的比例。注意,当使用信息熵 时,sklearn实际计算的是基于信息熵的信息增益(Information Gain),即父节点的信息熵和子节点的信息熵之差。
-
| 参数 | criterion |
|---|---|
| 如何影响模型 | 确定不纯度的计算方法,帮忙找出最佳节点和最佳分枝,不纯度越低,决策树对训练集 的拟合越好 |
| 可能的输入有哪些? | 不填默认基尼系数,填写gini使用基尼系数,填写entropy使用信息增益 |
怎样选取参数?
- 通常就使用基尼系数
- 数据维度很大,噪音很大时使用基尼系数
- 维度低,数据比较清晰的时候,信息熵和基尼系数没区别
- 决策树的拟合程度不够的时候,使用信息熵
- 两个都试试,不好就换另外一个
使用实例来理解不纯度
-
导入算法和库
from sklearn import tree #导入红酒模块 from sklearn.datasets import load_wine #导入训练测试集 from sklearn.model_selection import train_test_split探索数据
#给数据集命名为红酒 wine = load_wine() wine # 看到这个是个字典
如果wine是一张表应该长这样:
import pandas as pd
pd.concat([pd.DataFrame(wine.data),pd.DataFrame(wine.target)],axis = 1)
#这个就是特征的名字
wine.feature_names
['alcohol',
'malic_acid',
'ash',
'alcalinity_of_ash',
'magnesium',
'total_phenols',
'flavanoids',
'nonflavanoid_phenols',
'proanthocyanins',
'color_intensity',
'hue',
'od280/od315_of_diluted_wines',
'proline']
#这个是标签的名字
wine.target_names
array([‘class_0’, ‘class_1’, ‘class_2’], dtype=‘ 分出训练集和测试集 发现训练集124行,13个标签 原本的标签178行,13个标签 建立模型 score=0.9444444444444444 使用export_graphviz画一个树看看 通过上一条我们可以看出来,虽然我们给了决策树很多特征,但是他绘制这个表只选取了其中几个使用。所以我们可以得出:有些特征他是不那么重要的 下面我们来看一下每个特征的重要性: 这样观察不是很好看,所以采用下面这个函数: 所以我们把这些0.0的去掉对决策树也毫无影响 从上面我们对这个树的模型进行多次运行发现score经常不同,那么我们如何获得score最高的一次数据呢? 下面引入:random_state & splitter 只需要给上面的加一个out_file=“./tree.dot”,然后你的代码所在的文件夹内就会生成一个tree.dot文件。 但是此时在进行中文处理,打开这个tree.dot文件: 把这俩位置改成“SimHei”: 此时再win+R打开cmd,cd到dot文件所在文件夹,输入命令语句。 此时在你的tree.dot所在目录下就会生成了tree.png文件了 在不加限制的情况下,一棵决策树会生长到衡量不纯度的指标最优,或者没有更多的特征可用为止。**这样的决策 往往会过拟合,这就是说,它会在训练集上表现很好,在测试集上却表现糟糕。**我们收集的样本数据不可能和整体的状况完全一致,因此当一棵决策树对训练数据有了过于优秀的解释性,它找出的规则必然包含了训练样本中的噪声,并使它对未知数据的拟合程度不足。 sklearn中由很多不同的剪枝策略(max_depth–是用的最广泛的剪枝策略了) 我们的树对训练集的拟合程度如何? 1.0 (哈哈 过拟合了 为了让决策树有更好的泛化性,我们要对决策树进行剪枝。剪枝策略对决策树的影响巨大,正确的剪枝策略是优化决策树算法的核心。 超过设定深度的树枝全部剪掉。在高维度低样本量时非常有效。决策树多生长一层,对样本量的需求会增加一倍,所 以限制树深度能够有效地限制过拟合。在集成算法中也非常实用。实际使用时,建议从=3开始尝试,看看拟合的效 果再决定是否增加设定深度。 设置一下深度为3,也就是有4层: 此时发现: 看看决策树图像: 限制一下max_depth = 3,min_samples_leaf = 20: 此时发现: 看看决策树图像: 超参数的学习曲线,是一条以超参数的取值为横坐标,模型的度量指标为纵坐标的曲 线,它是用来衡量不同超参数取值下模型的表现的线。在我们建好的决策树里,我们的模型度量指标就是score。 发现: 结论: sklearn中许多算法的接口都是相似的,比如说我们之前已经用到的fit和score,几乎对每个算法都可以使用。除了 这两个接口之外,决策树最常用的接口还有apply和predict。 apply:apply中输入测试集返回每个测试样本所在的叶子节点的索引。 array([18, 28, 28, 28, 28, 8, 25, 18, 18, 28, 28, 26, 6, 15, 28, 15, 28, predict:predict输入测试集返回每个测试样本的标签。 array([1, 0, 0, 0, 0, 2, 1, 1, 1, 0, 0, 0, 1, 2, 0, 2, 0, 1, 0, 2, 1, 1, 在这里不得不提的是,所有接口中要求输入X_train和X_test的部分,输入的特征矩阵必须至少是一个二维矩阵。 sklearn不接受任何一维矩阵作为特征矩阵被输入。如果你的数据的确只有一个特征,那必须用reshape(-1,1)来给 矩阵增维;如果你的数据只有一个特征和一个样本,使用reshape(1,-1)来给你的数据增维。 至此,我们已经学完了分类树DecisionTreeClassifier和用决策树绘图(export_graphviz)的所有基础。我们讲解了决策树的基本流程,分类树的八个参数,一个属性,四个接口,以及绘图所用的代码。 八个参数:Criterion,两个随机性相关的参数(random_state,splitter),五个剪枝参数(max_depth, min_samples_split,min_samples_leaf,max_feature,min_impurity_decrease) 一个属性:feature_importances_ 四个接口:fit,score,apply,predict 有了这些知识,基本上分类树的使用大家都能够掌握了,接下来再到实例中去磨练就好。 几乎所有参数,属性及接口都和分类树一模一样。需要注意的是,在回归树种,没有标签分布是否均衡的问题,因 此没有class_weight这样的参数。 支持的标准有三种: 输入**“mse”**使用均方误差mean squared error(MSE),父节点和叶子节点之间的均方误差的差额将被用来作为 特征选择的标准,这种方法通过使用叶子节点的均值来最小化L2损失。 输入**“friedman_mse”**使用费尔德曼均方误差,这种指标使用弗里德曼针对潜在分枝中的问题改进后的均方误差。 输入**“mae”**使用绝对平均误差MAE(mean absolute error),这种指标使用叶节点的中值来最小化L1损失 属性中最重要的依然是feature_importances_。 在回归树中,MSE不只是我们的分枝质量衡量指标,也是我们最常用的衡 量回归树回归质量的指标,当我们在使用交叉验证,或者其他方式获取回归树的结果时,我们往往选择均方误差作 为我们的评估(在分类树中这个指标是score代表的预测准确率)。在回归中,我们追求的是,MSE越小越好。 然而,回归树的接口score返回的是R平方,并不是MSE。R平方被定义如下: u = ∑ i = 1 N ( f i − y i ) 2 u = \sum_{i=1}^{N}(f_i-y_i)^2 u=i=1∑N(fi−yi)2 v = ∑ i = 1 N ( y i − y ^ ) 2 v = \sum_{i=1}^N(y_i-\hat{y})^2 v=i=1∑N(yi−y^)2 其中u是残差平方和(MSE * N),v是总平方和,N是样本数量,i是每一个数据样本,fi是模型回归出的数值,yi 是样本点i实际的数值标签。y帽是真实数值标签的平均数。R平方可以为正为负(如果模型的残差平方和远远大于 模型的总平方和,模型非常糟糕,R平方就会为负),而均方误差永远为正。 值得一提的是,虽然均方误差永远为正,但是sklearn当中使用均方误差作为评判标准时,却是计算”负均方误 差“(neg_mean_squared_error)。这是因为sklearn在计算模型评估指标的时候,会考虑指标本身的性质,均 方误差本身是一种误差,所以被sklearn划分为模型的一种损失(loss),因此在sklearn当中,都以负数表示。真正的均方误差MSE的数值,其实就是neg_mean_squared_error去掉负号的数字。 接口依然是apply, fit, predict, score最核心。 交叉验证是用来观察模型的稳定性的一种方法,我们将数据划分为n份,依次使用其中一份作为测试集,其他n-1份 作为训练集,多次计算模型的精确性来评估模型的平均准确程度。训练集和测试集的划分会干扰模型的结果,因此 用交叉验证n次的结果求出的平均值,是对模型效果的一个更好的度量。 接下来我们到二维平面上来观察决策树是怎样拟合一条曲线的。我们用回归树来拟合正弦曲线,并添加一些噪声来观察回归树的表现。 导入需要的库 创建一条 代码解释: 实例化&训练模型 做两个是为了观察不同深度下的回归树的效果对比 测试集导入模型,预测结果 (4, 1) 绘制图像 结论: 可见,回归树学习了近似正弦曲线的局部线性回归。我们可以看到,如果树的最大深度(由max_depth参数控制) 设置得太高,则决策树学习得太精细,它从训练数据中学了很多细节,包括噪声得呈现,从而使模型偏离真实的正弦曲线,形成过拟合。 富文本语言 导入需要的库 导入数据集,探索数据 发现数据集是一个891行*12列的表格 使用head()和info()探索数据: 显示前100行,一般是默认5 info():显示每一列详细信息的: 对数据预处理 step1:筛选特征 删除缺失值过多的列和观察判断来说和预测的y没有关系的列 然后现在再观察一下我们的data: 确实少了三列。 step2:处理缺失值 对缺失值进行列填补 有些数值型变量可以使用平均值进行填补,比如年龄 有些特征值只有一两个值缺省,那直接把这两行删掉就行。 step3:把Sex和Embarked转化为数字 此时观察可知,基本所有数据都已填满。**但是因为决策树无法处理文字,**所以我们需要把Sex和Embarked转化为数字: array([‘S’, ‘C’, ‘Q’], dtype=object) [‘S’, ‘C’, ‘Q’] 0 上面相当于 上面的这种方式是非常好的把标签转化为数字的一种方式,前提是: 另一种转换方法:但是只能应用到二分类 至此,我们的数据预处理已经完成! 提取标签和特征矩阵,分测试集和训练集 因为特征和标签是分开导入的,所以我们使用iloc来进行导入 下面开始训练! 但是发现经过了train_test_split训练以后,我们发现训练集的索引变乱了,必须得把他变有序,不然后面训练很难进行下去。 通过Xtrain.index我们发现他的标签确实都变乱了。 通过*range(Xtrain.shape[0])*改变! 我的是0.700374531835206,每个人的都不一样。不一样的原因是因为最开始训练分数据集和训练集的时候*(train_test_split(x,y,test_size=0.3)*这个是随机分的,所以每个人的随机数都不一样就会导致最终的测试分数也不一样。 不过这个分数太低了实在是,所以我们使用交叉验证来提高一下分数! 0.6536389172625128 哈哈,这说明我们之前随机分配的训练集和测试集还是挑的高的分的,所以就导致取平均后跟别的平摊以后更低了。 在不同max_depth下观察模型的拟合状况 *print(max(te))*输出的是最高的测试集分数我们由草参数学习曲线可以发现是在max_depth=6时取得的 为什么要画两条曲线? 网格搜索技术:能够帮助我们同时调整多个参数的技术。是枚举技术 因为他是枚举技术,把参数一个个试过去,所以计算量非常大,十分耗时间。所以我们在进行网格搜索的时候,必须先预定一个参数范围,可不能让参数范围从正无穷到负无穷,电脑该爆炸了。 此时我们使用的例子还是上面的泰坦尼克号的幸存者预测数据: 下面开始进行网格搜索,速度挺慢的得需要几分钟: 此时我们通过best_params_可以观察到最好的参数组合是: 此时我们通过best_score_可以观察到最好的分数是: 于训练集说明我们的模型欠拟合,所以我们就把模型多修正到能拟合到训练集上 网格搜索技术:能够帮助我们同时调整多个参数的技术。是枚举技术 因为他是枚举技术,把参数一个个试过去,所以计算量非常大,十分耗时间。所以我们在进行网格搜索的时候,必须先预定一个参数范围,可不能让参数范围从正无穷到负无穷,电脑该爆炸了。 此时我们使用的例子还是上面的泰坦尼克号的幸存者预测数据: 下面开始进行网格搜索,速度挺慢的得需要几分钟: 结果: 此时我们通过best_params_可以观察到最好的参数组合是: 此时我们通过best_score_可以观察到最好的分数是: 但是这并不一定是决策树的最好的参数组合。因为有的时候我们的参数给的太多了,而网格搜索并不会舍弃我们的参数,会导致网格搜索的时候每个参数他都用上。然后反而会导致我们的分数下降。
Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size = 0.3)
Xtrain.shape
wine.data.shape
# 实例化一下
clf = tree.DecisionTreeClassifier(criterion = "entropy")
#训练一下
clf = clf.fit(Xtrain, Ytrain)
#测试一下
score = clf.score(Xtest, Ytest)
score
feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类','花青素','颜色强度','色调','od280/od315稀释葡萄酒','脯氨酸']
import graphviz
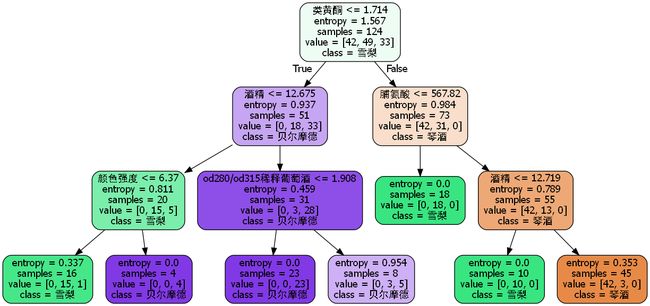
dot_data = tree.export_graphviz(clf
,feature_names = feature_name
,class_names = ["琴酒","雪梨","贝尔摩德"]
,filled = True# 用颜色表示不同分类
,rounded = True# 不加就变成方的啦,一般都用圆角
)
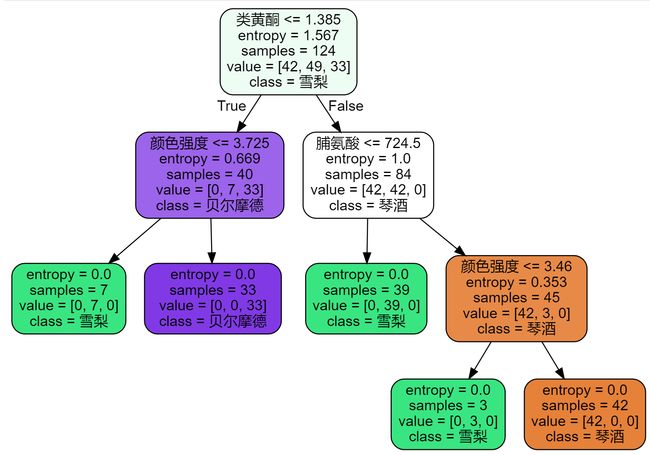
graph = graphviz.Source(dot_data)
graph
clf.feature_importances_
[*zip(feature_name,clf.feature_importances_)]
2.1.2 random_state & splitter
clf = tree.DecisionTreeClassifier(criterion = "entropy"
,random_state = 30
,splitter = "random"
)
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest)
score
feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类','花青素','颜色强度','色调','od280/od315稀释葡萄酒','脯氨酸']
import graphviz
dot_data = tree.export_graphviz(clf
,feature_names = feature_name
,class_names = ["琴酒","雪梨","贝尔摩德"]
,filled = True# 用颜色表示不同分类
,rounded = True# 不加就变成方的啦,一般都用圆角
)
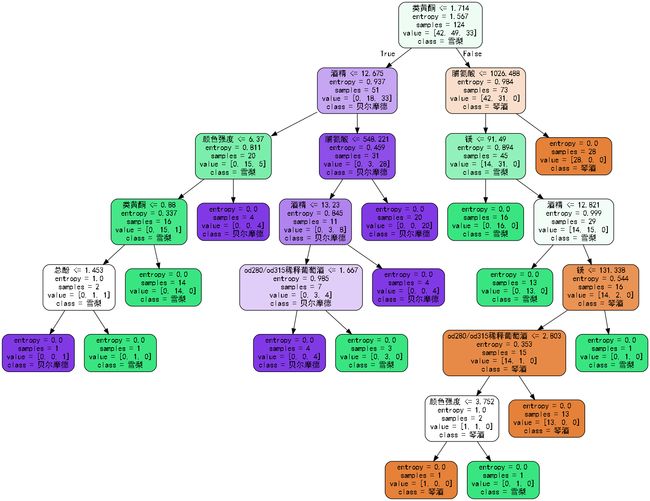
graph = graphviz.Source(dot_data)
graph
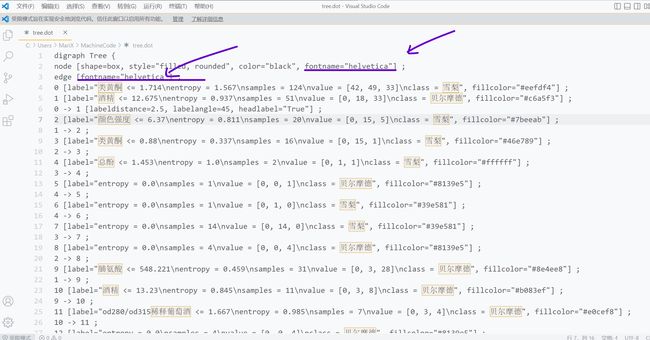
补充graphviz生成的tree.dot怎么变成graphviz以及中文乱码问题:
dot_data = tree.export_graphviz(clf
,feature_names = feature_name
,class_names = ["琴酒","雪梨","贝尔摩德"]
,filled = True# 用颜色表示不同分类
,rounded = True# 不加就变成方的啦,一般都用圆角
,out_file="./tree.dot"
)
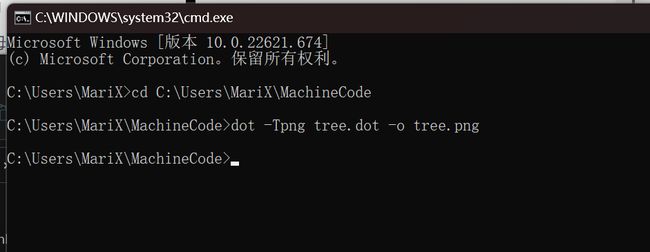
dot -Tpng tree.dot -o tree.png
# -T的意思是生成的文件是png格式的
# -o指定生成的文件名
# tree.dot为dot形式名称,tree.png为图片png形式名称
2.1.3 剪枝参数
score_train = clf.score(Xtrain,Ytrain)
score_train
2.1.3.1 max_depth --限制树的最大深度
clf = tree.DecisionTreeClassifier(criterion = "entropy"
,random_state = 30
,max_depth = 3
,splitter = "random"
)
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest)
print("score=",score)
score_train = clf.score(Xtrain,Ytrain)
print("score_train=",score_train)
feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类','花青素','颜色强度','色调','od280/od315稀释葡萄酒','脯氨酸']
import graphviz
dot_data = tree.export_graphviz(clf
,feature_names = feature_name
,class_names = ["琴酒","雪梨","贝尔摩德"]
,filled = True# 用颜色表示不同分类
,rounded = True# 不加就变成方的啦,一般都用圆角
)
graph = graphviz.Source(dot_data)
graph
2.1.3.2 min_samples_leaf --限制节点后的子节点
clf = tree.DecisionTreeClassifier(criterion = "entropy"
,random_state = 30
,max_depth = 3
,min_samples_leaf = 20
,splitter = "random"
)
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest)
print("score=",score)
score_train = clf.score(Xtrain,Ytrain)
print("score_train=",score_train)
feature_name = ['酒精','苹果酸','灰','灰的碱性','镁','总酚','类黄酮','非黄烷类酚类','花青素','颜色强度','色调','od280/od315稀释葡萄酒','脯氨酸']
import graphviz
dot_data = tree.export_graphviz(clf
,feature_names = feature_name
,class_names = ["琴酒","雪梨","贝尔摩德"]
,filled = True# 用颜色表示不同分类
,rounded = True# 不加就变成方的啦,一般都用圆角
)
graph = graphviz.Source(dot_data)
graph
2.1.3.3 max_features & min_impurity_decrease --限制特征个数
2.1.4 使用超参数的学习曲线和网格搜索技术确认最优剪枝参数
2.1.4.1 超参数学习曲线
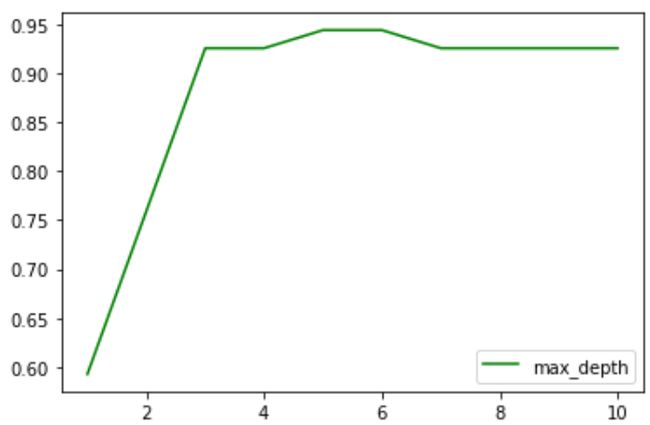
import matplotlib.pyplot as plt
test = []
for i in range(10):
clf = tree.DecisionTreeClassifier(criterion = "entropy"
,random_state = 30
,max_depth = i+1
,splitter = "random"
)
clf = clf.fit(Xtrain, Ytrain)
score = clf.score(Xtest, Ytest)
test.append(score)
plt.plot(range(1,11),test,color = "green",label = "max_depth")
plt.legend()
plt.show()
2.1.4.2 网格搜索技术
2.2 重要属性和接口
clf.apply(Xtest)
20, 28, 14, 20, 20, 18, 28, 28, 18, 20, 6, 15, 7, 18, 18, 5, 20,
15, 26, 15, 20, 26, 15, 15, 20, 7, 28, 28, 15, 15, 15, 18, 7, 15,
18, 18, 7], dtype=int64)clf.predict(Xtest)
1, 0, 0, 1, 1, 1, 2, 1, 1, 1, 2, 1, 2, 0, 2, 1, 0, 2, 2, 1, 1, 0,
0, 2, 2, 2, 1, 1, 2, 1, 1, 1])
三、DecisionTreeRegressor–回归树
class sklearn.tree.DecisionTreeRegressor (criterion=’mse’, splitter=’best’, max_depth=None,
min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None,
random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, presort=False)
3.1 重要参数、属性和接口
3.1.1 criterion–回归树衡量分枝质量的指标
M S E = 1 N ∑ i = 1 N ( f i − y i ) 2 MSE = \frac{1}{N}\sum_{i=1}^N(f_i-y_i)^2 MSE=N1i=1∑N(fi−yi)2
其中N是样本数量,i是每一个数据样本,fi是模型回归出的数值,yi是样本点i实际的数值标签。所以MSE的本质, 其实是样本真实数据与回归结果的差异。
R 2 = 1 − u v R^2=1-\frac{u}{v} R2=1−vu3.1.2 交叉验证
3.2 用回归树拟合正弦曲线实例
3.2.1 一维回归的图像绘制
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
rng = np.random.RandomState(1)
X = np.sort(5*rng.rand(80,1),axis=0)
Y = np.sin(X).ravel()
#添加干扰点:
Y[::5] = Y[::5] + 3*(0.5 - rng.rand(16))
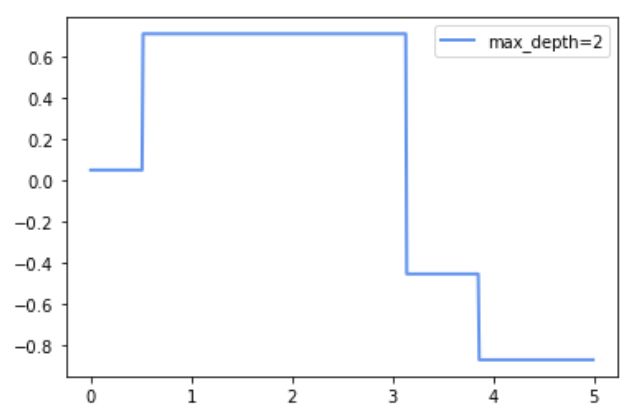
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X,Y)
regr_2.fit(X,Y)
X_test = np.arange(0.0,5.0,0.01)[:,np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
# np.arrange(开始点,结束点,步长) 生成有序数组的函数
l = np.array([1,2,3,4])
l[:,np.newaxis].shape
plt.figure()
plt.scatter(X,Y,s=20,edgecolor="black",c="darkorange", label="data")
plt.legend()
plt.show()
plt.plot(X_test,y_1,color="cornflowerblue",label="max_depth=2",linewidth=2)
plt.legend()
plt.show()
plt.plot(X_test,y_2,color="yellowgreen",label="max_depth=2",linewidth=2)
plt.legend()
plt.show()
plt.scatter(X,Y,s=20,edgecolor="black",c="darkorange", label="data")
plt.plot(X_test,y_1,color="cornflowerblue",label="max_depth=2",linewidth=2)
plt.plot(X_test,y_2,color="yellowgreen",label="max_depth=2",linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
3.2.2 kaggle泰坦尼克号幸存者的预测
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
data = pd.read_csv(r"C:\Users\MariX\MachineCode\data.csv")
data
data.head(100)
data.info()
data.drop(["Cabin","Name","Ticket"],inplace=True,axis=1)
# inplace=True,是删除完以后覆盖原表。默认False;
# axis=1是对列进行操作
data
data["Age"] = data["Age"].fillna(data["Age"].mean())
data.info()
data = data.dropna(axis = 0)
# dropna是删掉所有有缺失值的数据
# axis = 0是删掉一行,默认0,=1时删除一列
data.info()
data["Embarked"].unique()
# unique()可以去掉重复取值,看看总共有几种取值方式
# 可以看出这是一个数组,我们把它变成一个列表
data["Embarked"].unique().tolist()
# 给labels加上标签
labels = data["Embarked"].unique().tolist()
data["Embarked"] = data["Embarked"].apply(lambda x: labels.index(x))
labels.index("S")
“S” -->labels.index(“S”)
data
# 这句话是把Sex里面本来显示True和False的都变成显示1和0
(data["Sex"] == "male").astype(int)
data["Sex"] = (data["Sex"] == "male").astype(int)
# 不过上面的方法快删除了,用这种loc方法
# loc是文字索引,不过他是标签索引只能用表头。使用数字索引就用iloc
data.loc[:,"Sex"] = (data["Sex"] == "male").astype(int)
data.head()
x = data.iloc[:,data.columns != "Survived"]
x = x.iloc[:,x.columns != "PassengerId"]
x
# 这是布尔索引
# 可以发现x中没有Survived这一列了
y = data.iloc[:,data.columns == "Survived"]
y
# 取出标签为Survived这一列
Xtrain,Xtest,Ytrain,Ytest = train_test_split(x,y,test_size=0.3)
Xtrain
# 发现索引变乱
Xtrain.index
Int64Index([403, 45, 658, 652, 604, 367, 457, 156, 683, 262,
...
679, 562, 889, 209, 137, 228, 862, 688, 493, 389],
dtype='int64', length=622)
Xtrain.index = range(Xtrain.shape[0])
Xtrain#变回来了
# 其他几个也这样:
for i in [Xtrain,Xtest,Ytrain,Ytest]:
i.index = range(i.shape[0])
Ytrain
clf = DecisionTreeClassifier(random_state = 25)
clf = clf.fit(Xtrain,Ytrain)
score = clf.score(Xtest,Ytest)
score
clf = DecisionTreeClassifier(random_state=25)
score = cross_val_score(clf,x,y,cv=10).mean()
score
tr = []
te = []
for i in range(10):
clf = DecisionTreeClassifier(random_state=25
,max_depth=i+1
,criterion = "entropy"
)
clf = clf.fit(Xtrain,Ytrain)
score_tr = clf.score(Xtrain,Ytrain)
score_te = cross_val_score(clf,x,y,cv=10).mean()
tr.append(score_tr)
te.append(score_te)
print(max(te))
plt.plot(range(1,11),tr,color="red",label="train")
plt.plot(range(1,11),te,color="blue",label="test")
plt.xticks(range(1,11))# 不写他就不会全显示出来
plt.legend()
plt.show()
3.3 网格搜索技术
import numpy as np
gini_thresholds = np.linspace(0,0.5,20)
parameters = {'splitter':('best','random')
,'criterion':("gini","entropy")
,"max_depth":[*range(1,10)]
,'min_samples_leaf':[*range(0,50,5)]
,'min_impurity_decrease':[*np.linspace(0,0.5,20)]
}
clf = DecisionTreeClassifier(random_state=25)
GS = GridSearchCV(clf, parameters, cv=10)
GS.fit(Xtrain,Ytrain)
GS.best_params_
GS.best_score_
4. 如果训练集曲线远高于测试集,那说明我们的模型就是过拟合的,在训练集上表现得很好,但是在测试集中却表现得很糟糕。所以我们需要剪枝。3.3 网格搜索技术
import numpy as np
gini_thresholds = np.linspace(0,0.5,20)
parameters = {'splitter':('best','random')
,'criterion':("gini","entropy")
,"max_depth":[*range(1,10)]
,'min_samples_leaf':[*range(0,50,5)]
,'min_impurity_decrease':[*np.linspace(0,0.5,20)]
}
clf = DecisionTreeClassifier(random_state=25)
GS = GridSearchCV(clf, parameters, cv=10)
GS.fit(Xtrain,Ytrain)
GridSearchCV(cv=10, estimator=DecisionTreeClassifier(random_state=25),
param_grid={‘criterion’: (‘gini’, ‘entropy’),
‘max_depth’: [1, 2, 3, 4, 5, 6, 7, 8, 9],
‘min_impurity_decrease’: [0.0, 0.02631578947368421,
0.05263157894736842,
0.07894736842105263,
0.10526315789473684,
0.13157894736842105,
0.15789473684210525,
0.18421052631578946,
0.21052631578947367,
0.23684210526315788,
0.2631578947368421,
0.2894736842105263,
0.3157894736842105,
0.3421052631578947,
0.3684210526315789,
0.39473684210526316,
0.42105263157894735,
0.4473684210526315,
0.47368421052631576, 0.5],
‘min_samples_leaf’: [0, 5, 10, 15, 20, 25, 30, 35, 40,
45],
‘splitter’: (‘best’, ‘random’)})GS.best_params_
{‘criterion’: ‘gini’,
‘max_depth’: 5,
‘min_impurity_decrease’: 0.0,
‘min_samples_leaf’: 15,
‘splitter’: ‘random’}GS.best_score_
0.7138760880696365