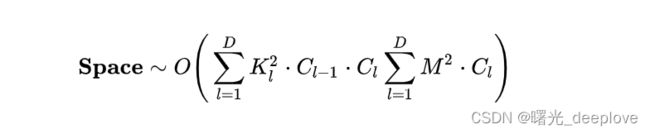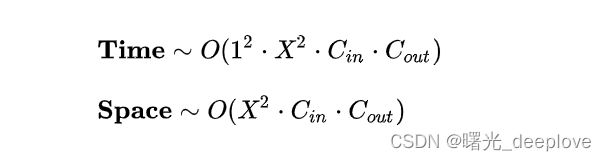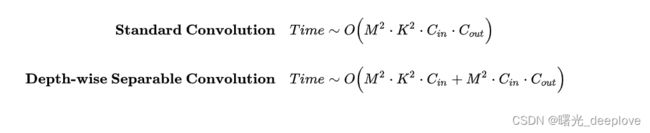深度学习模型参数量/计算量和推理速度计算(二)
本文学习记录卷积神经网络的复杂度分析。
转载自:卷积神经网络的复杂度分析 - 知乎
卷积神经网络的复杂度分析
在梳理CNN经典模型的过程中,我理解到其实经典模型演进中的很多创新点都与改善模型计算复杂度紧密相关,因此今天就让我们对卷积神经网络的复杂度分析简单总结一下。
本文主要关注的是针对模型本身的复杂度分析(其实并不是很复杂啦~)。如果想要进一步评估模型在计算平台上的理论计算性能,则需要了解 Roofline Model 的相关理论,欢迎阅读本文的进阶版: Roofline Model与深度学习模型的性能分析。
一、时间复杂度(FLOPs)
即模型的运算次数,可用FLOPs衡量,也就是浮点运算次数(Float-point Operations)。
1.1 单个卷积层的时间复杂度
M:每个卷积核输出特征图(Feature Map)的边长
K:每个卷积核(Kernel)的边长
Cin :上一层的输出通道数,本层的输入通道数
Cout: 本卷积层具有的卷积核个数,也即输出通道数
每个卷积层的时间复杂度由:输出特征图面积![]() 、卷积核面积
、卷积核面积![]() 、输入
、输入![]() 和输出通道数
和输出通道数![]()
完全决定(具体计算也考参考另一篇文章的FLOPs计算)。
其中,输出特征图尺寸(计算方法参考:链接)本身又由:输入矩阵尺寸X、卷积核尺寸K、Padding、Stride这四个参数所决定,表示如下:
![]()
注1:为了简化表达式中的变量个数,这里统一假设卷积操作的输入和卷积核本身的形状均是正方形的。
注2:严格来讲每层应该还包含1个Bias参数,这里为了简洁就省略了。
这里给出:
在计算机视觉论文中,常常将一个'乘-加'组合视为一次浮点运算,英文表述为'Multi-Add',运算量正好是上面的算法减半,此时的运算量(考虑bias)为:
因此就有了:
其中上面的H*W就是![]() ,是卷积后的输出特征图的尺寸。
,是卷积后的输出特征图的尺寸。
从FLOPs的计算公式也可以看到,其只与输出特征图面积![]() 、卷积核面积
、卷积核面积![]() 、输入
、输入![]() 和输出通道数
和输出通道数![]() 有关!!!
有关!!!
1.2 卷积神经网络整体的时间复杂度
示例:用 Numpy 手动简单实现二维卷积
from calendar import c
import numpy as np
import cv2
"""
假设 Stride = 1, Padding = 0, img 和 kernel 都是 np.ndarray.
卷积计算公式:Wnew = {(W - F + 2 * P) / S} + 1
"""
def conv2d(pic, k):
height, width, in_channels = pic.shape
kernel_height, kernel_width, kernel_in_channels, kernel_out_channels = k.shape
print("kernel_height is {}, kernel_width is {}, kernel_in_channels is {}, \
kernel_out_channels is {}".format(kernel_height, kernel_width,
kernel_in_channels,
kernel_out_channels))
out_height = height - kernel_height + 1 # 经过卷积计算公式
out_width = width - kernel_width + 1 # 经过卷积计算公式
feature_maps = np.zeros(shape=(out_height, out_width,
kernel_out_channels)) #创建(初始化)全0的特征输出图
for oc in range(kernel_out_channels):
for h in range(out_height):
for w in range(out_width):
for ic in range(
kernel_in_channels): #kernel_in_channels即为上一层特征输出时的通道
# patch就是取卷积核大小的roi区域,用于与卷积核进行计算(对应元素相乘再相加)
# patch的shape:(10 ,3),取ic通道后就从3通道变成了单通道的图
patch = pic[
h:h + kernel_height, w:w + kernel_width,
ic] #切片 + 索引,取第ic个通道,高宽大小分别为:h至h + kernel_height,w至w + kernel_width
t = k[:, :, ic,
oc] #t的shape:(10 ,3);kernel的shape:(10, 3, 3, 3),也是取索引后变成了单通道的
feature_maps[h, w, oc] += np.sum(patch * k[:, :, ic, oc])
#print(111)
return feature_maps
if __name__ == "__main__":
img = cv2.imread("2.png")
kernel = np.random.randn(3, 3, 3, 3) #卷积核shape:[b, h, w, c]
f = conv2d(img, kernel)
print(f)二、空间复杂度
空间复杂度也叫访存量,严格来讲包含两部分:总参数量 + 各层输出特征图。
1)参数量:模型所有带参数的层的权重参数总量(即模型体积,下式第一个求和表达式)
2)特征图:模型在实时运行过程中每层所计算出的输出特征图大小(下式第二个求和表达式)
3)总参数量只与卷积核的尺寸K、通道数C、层数D相关,而与输入数据的大小无关。
4)输出特征图的空间占用比较容易,就是其空间尺寸![]() 和通道数C的连乘。
和通道数C的连乘。
注:实际上有些层(例如ReLU)其实是可以通过原位运算完成的,此时就不用统计输出特征图这一项了。
三、复杂度对模型的影响
1)时间复杂度决定了模型的训练/预测时间。如果复杂度过高,则会导致模型训练和预测耗费大量时间,既无法快速的验证想法和改善模型,也无法做到快速的预测。
2)空间复杂度决定了模型的参数数量。由于维度诅咒的限制,模型的参数越多,训练模型所需的数据量就越大,而现实生活中的数据集通常不会太大,这会导致模型的训练更容易过拟合。
3)当我们需要裁剪模型时,由于卷积核的空间尺寸通常已经很小(3x3),而网络的深度又与模型的表征能力紧密相关,不宜过多削减,因此模型裁剪通常最先下手的地方就是通道数。
四、Inception系列模型是如何优化复杂度的
通过五个小例子说明模型的演进过程中是如何优化复杂度的。
4.1 InceptionV1中的1x1卷积降维同时优化时间复杂度和空间复杂度
(1)InceptionV1借鉴了Network in Network的思想,在一个Inception Module中构造了四个并行的不同尺寸的卷积/池化模块(上图左),有效的提升了网络的宽度。但是这么做也造成了网络的时间和空间复杂度的激增。对策就是添加1x1卷积(上图右红色模块)将输入通道数先降到一个较低的值,再进行真正的卷积。
(2)以InceptionV1论文中的(3b)模块为例,输入尺寸为28x28x256,1x1卷积核128个,3x3卷积核192个,5x5卷积核96个,卷积核一律采用Same Padding确保输出不改变尺寸。
(3)在3x3卷积分支上加入64个1x1卷积前后的时间复杂度对比如下式:
Before: ![]()
After:![]()
(4)同理,在5x5卷积分支上加入64个1x1卷积前后的时间复杂度对比如下式:
Before: ![]()
After:![]()
从上面可见:使用1x1卷积降维可以降低时间复杂度3倍以上。该层完整的运算量可以在论文中查到为300M,即![]() 。
。
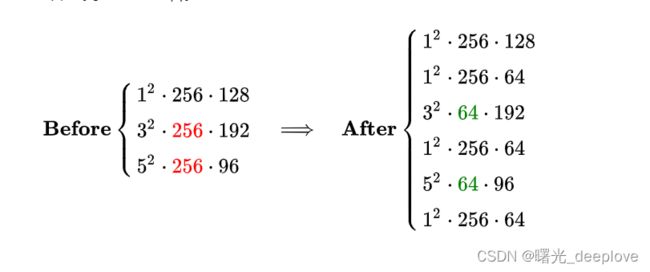
另一方面空间复杂度上,我们同样可以简单分析一下这一层参数量(空间复杂度)在使用1x1卷积前后的变化。可以看到由于1x1卷积的添加,3x3和5x5卷积核的参数量得以降低4倍,因此本层的参数量(计算方法参考我自己的文章:yolo学习之骨干网络推导)从1000k降低到300k左右。
4.2 InceptionV1中使用GAP代替Flatten
全连接层可以视为一种特殊的卷积层,其卷积核尺寸K与输入矩阵尺寸X一模一样。每个卷积核的输出特征图是一个标量点,即M=1(M表示卷积后的特征图)。时间复杂度和空间复杂度分析如下:
可见,与真正的卷积层不同,全连接层的空间复杂度与输入数据的尺寸密切相关。因此如果输入图像尺寸越大,模型的体积也就会越大,这显然是不可接受的。例如早期的VGG系列模型,其 90% 的参数都耗费在全连接层上。
InceptionV1 中使用的全局平均池化 GAP 改善了这个问题。由于每个卷积核输出的特征图在经过全局平均池化后都会直接精炼成一个标量点,因此全连接层的复杂度不再与输入图像尺寸有关,运算量和参数数量都得以大规模削减。复杂度分析如下:
参考:神经网络改进方案:全局平均池化替代全连接层_深度瞎学的博客-CSDN博客_全局平均池化代替全连接层
4.3 InceptionV2中使用两个3x3卷积级联替代5x5卷积分支
感受野不变
(1)根据上面提到的二维卷积输入输出尺寸关系公式,可知:对于同一个输入尺寸,单个5x5 卷积的输出与两个 3x3卷积级联输出的尺寸完全一样,即感受野相同。
(2)同样根据上面提到的复杂度分析公式,可知:这种替换能够非常有效的降低时间和空间复杂度。我们可以把辛辛苦苦省出来的这些复杂度用来提升模型的深度和宽度,使得我们的模型能够在复杂度不变的前提下,具有更大的容量,爽爽的。
(3)同样以InceptionV1里的(3b)模块为例,替换前后的5x5卷积分支复杂度如下:
4.4 InceptionV3中使用Nx1与1XN卷积级联替代NxN卷积
1)InceptionV3 中提出了卷积的 Factorization(卷积操作的分解步骤),在确保感受野不变的前提下进一步简化
2)复杂度的改善同理可得,不再赘述。
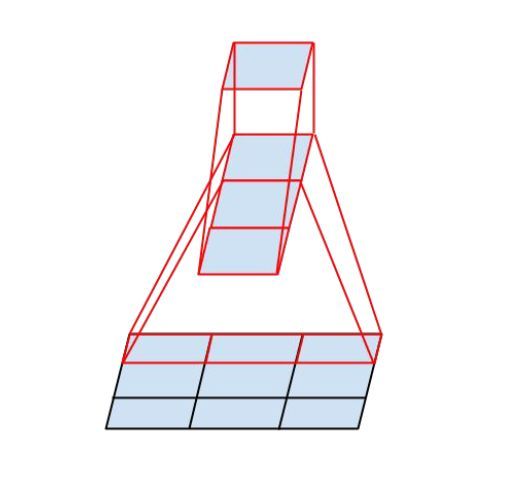
4.5 Xception中使用Depth-wise Separable Convolution
Depth-wise Separable Convolution:深度可分离卷积
1)我们之前讨论的都是标准卷积运算,每个卷积核都对输入的所有的通道进行卷积。
2)Xception模型挑战了这个思维定势,它让每个卷积核只负责输入的某一个通道,这就是所谓的 深度可分离卷积。
注:原始标准的卷积是每个卷积核都去卷积各通道:
3)从输入通道的视角看,标准卷积中每个输入通道都会被所有卷积蹂躏一遍,而Xception中每个输入通道都只会被对应的一个卷积核扫描,降低了模型的冗余度。
4)标准卷积与深度可分离卷积的时间复杂度对比:可以看到本质上是把连乘转化为相加。
五、总结
通过上面的推导和经典模型的案例分析,我们可以清楚的看到其实很多创新点都是围绕模型复杂度的优化展开的,其基本逻辑就是乘变加。模型的优化换来了更少的运算次数和更少的参数数量,一方面促使我们能够构建更轻更快的模型(例如MobileNet),一方面促使我们能够构建更深更宽的网络(例如Xception)。
注:本文主要关注的是针对模型本身的复杂度分析。如果想要进一步评估模型在计算平台上的理论计算性能,则需要了解 Roofline Model 的相关理论,欢迎阅读本文的进阶版: Roofline Model与深度学习模型的性能分析。
update补充:
Q1:请问能不能解释一下Depth-wise Separable Convolution的时间复杂度?M*M*Cin*Cout是1x1卷积的时间复杂度,输出的是Cout个feature map,再用Cout个3x3的卷积核分别对输出的feature map做卷积,时间复杂度不应该是M*M*3*3*Cout吗,为什么时间复杂度公式里是Cin?谢谢啦。
A1:Depthwise Separable 是一个 Depthwise conv 加一个 Pointwise conv,其中 Depthwise 是 M*M*K*K*Cin,Pointwise 是 M*M*Cin*Cout。
Q2:写的很好!令我对网络的细节有了更多的认识!有一个问题,与Miracle的类似。您所使用的复杂度的公式暗示了卷积核是2维(K*K)的,所以一个卷积核的参数是w1,w2,...,wK^2, 一共K^2个,又因为输出通道数=卷积核的个数,所以卷积层整体的参数数量是$K^2 \times 总体通道数$。 所以我认为您的空间复杂度不需要再乘以$C_(l-1)$ 了。
A2:由于输入特征图总是三维的,因此单个卷积核也是三维的,尺寸为 K*K*Cin,卷积层也就是四维的,尺寸为 K*K*Cin*Cout。
Q3:Gap 按照全局池化考虑 是不是时间复杂度应该是 M*M*C_in*C_out? M表示gap的输入特征图边长
A3:应该是的。GAP其实就是每个M*M*C_in 全部求和再求平均,一共进行Cout次。
Q4:楼主你好,非常精彩的讲解,有一个问题如下:
关于空间复杂度,每一层的输入与输出数据(feature map)为何都没有考虑?每一层的feature map也是同样要占用大量空间的吧?
考虑到feature map大小与输入大小和卷积大小相关,因此
与输入数据的大小无关。
这句似乎就不太对了?
A4:感谢你的提醒!看来我之前对于模型的空间复杂度理解的还不够深入。模型的空间复杂度确实应该考察两个维度,一个是模型的参数数量(也就是文中提到的模型存储在硬盘上的体积),另一个则是我之前忽视掉的模型的访存量(模型在运行时实际发生的内存交换,等于模型的参数量与每层输出特征图的内存占用之和)。后者会影响模型在计算平台上的实际运行速度。
Q5:
(1)请问空间复杂度为什么要乘以输入channel数量,应该只需要乘以输出channel数量吧,还望指点
A5:因为每个卷积核所具有的通道数一定等于输入数据的通道数,所以每个卷积核的参数数量就应该是W * H * C,然后再乘以卷积核的数量,就是这一层整体的参数数量了。
(2) 卷积的实现是每个卷积核都依次和输入通道相乘,最后相加得到结果。所以参数数量应该不用乘以输入通道,因为此时卷积核参数是共享的,一共几个卷积核就乘以几就行,你说呢?
A5:标准卷积中,假设输入有三个通道,那么每个卷积核也会有三个通道,卷积时需要计算三个通道的点积之和。你说的是Xception的情况,每个卷积核只有一个通道,只负责和输入的一个通道卷积。我理解“参数共享”并不是指不同通道共享参数,而是指输入图片同一通道上的不同像素会遇到相同的权重。是相对于全链接这种一个萝卜一个坑的权重而言的。
把这个可视化动图推荐给你 Convolution demo
Q6:你好,使用深度可分离卷积的模型会比常规卷积更深,更多的中间feature map,空间复杂度反而更大,这在内存占用和gpu利用率上会更高,这样的话怎么还被称为轻量级网络呢?会不会出现,一个设备上本来可以同时跑4个模型,使用了深度可分离卷积后只能跑三个?
A6:这个需要定量分析,比如把mobilenet的dw/pw都换成标准卷积,在层数、输入尺寸都基本一致的情况下在不同平台上测。dw卷积其实就是以降低计算强度为代价来降低计算量,使得模型在单位访存字节数下所做的计算量下降,从而让低算力设备从算力受限状态向访存受限状态移动,对于原本算力就很强的平台而言并没有显著的益处。