机器人手眼标定详解
手眼标定详解
研究现状
所谓手眼标定是统一视觉系统和机器人的坐标系,从而可以使视觉系统所确定的物体位姿可以转换到机器人坐标系下,由机械臂完成对物体的作业。
最常见的手眼系统包括Eye-to-Hand和Eye-in-Hand两种。在Eye-to-Hand手眼系统中,摄像机与机器人基座的位置是相对固定的,手眼关系式求解摄像机坐标系与机器人基座坐标系之间的转换关系。在Eye-in-Hand手眼系统中,摄像机由于固定在机械臂末端,手眼关系求解的是摄像机坐标系与机械臂末端坐标系之间的转换关系。在机器人处于不同的位置和姿态的情况下,获取“眼”相对于标定物的关系。然后结合机器人的位姿(可以从机器人控制器上读出),就能建立标定方程 A X = X B AX=XB AX=XB,求解方程就能得到手眼关系矩阵。 在求解标定方程 A X = X B AX=XB AX=XB时,由于方程求解的非线性和不稳定,如何求得一个误差小而且有意义的解是手眼标定的重要问题。关于如何求解的问题,就有了许多不同的手眼标定方法。 对手眼换矩阵的求解主要有两类方法。
一类方法利用旋转矩阵的性质把非线性化的问题线性化。这类方法均包含两个阶段:首先通过线性化的方法求解手眼变换矩阵的旋转部分,然后将旋转部分的求解结果代入手眼方程,求解手眼矩降的平移部分,这类方法可以推导出简单且求解方便的线性求解方程,但是由于是分两步束解,旋转矩阵参数的估计误差会传递到平移向量中,因此对观测数据中的噪声敏感。这类方法可以得出唯一解的充分条件是至少有两次机械臂运动的旋转轴是非平行的。这类方法中Shui的方法是通过两次移动机械臂来计算手眼变换矩阵。Tsai将问题分解成两部分,即将旋转平移矩阵分解成旋转和平移两部分进行求解,先求解旋转矩阵,再将旋转矩阵代入求解平移向量。在后来的研究中lee给出了简化求解方程的方法,Strobl对此问题做了优化。Daniilidis采用对偶四元数来表示空间的运动。Chou和Kamel提出的方法基于奇异值分解SVD。对于在线手眼标定,Andreff提出的方法给出了一种新的手眼关系的线性化方程,以实现数学上的高效计算,满足在线标定对实时性的需求。
另一类是采用优化的方法求解非线性问题。这类方法需要束解复杂的非线性优化问题,通常计算量相对较大,求解耗时,不能满足在线实时计算的需求。而且非线性优化的结果依赖于初值的选择,选择不当的初值,会陷入局部最优,无法得到全局最优解。在这类方法中,zhuang将机器人手眼系统与机器人执行器作为一个整体进行建模,并应用非线性优化的方法求解旋转矩阵和平移向量,以最小化手眼变换矩阵误差的Frobenius范数作为优化目标。wei提出了一种方法,这种方法无需借助标定工具,且可以同时完成手眼标定和摄像机标定。Ilonen采用了标记点定位的方法,但需要已知摄像机内参。
通过调研,决定使用Chou和Kamel方法,该方法能实现所需功能,且实现过程相对简洁,方便程序实现和维护。
问题描述
问题描述:本题目中的手眼系统为Eye-to-Hand。在eye to hand手眼系统中 ,采集了机器人N组位姿下, 末端坐标系{tool}在基坐标系{base}下位置及姿态T_b_t, 标定板坐标系{cal}在相机坐标系{cam}下的位置及姿态T_c_cal。求基坐标系的到相机坐标系齐次坐标变换 b a s H c a m ^{bas}H_{cam} basHcam。
求解说明
任意运动中,机器人末端到标定板的位姿关系 t o o l H c a l ^{tool}H_{cal} toolHcal保持不变,基坐标系到相机坐标系的位姿关系保持不变 b a s e H c a m ^{base}H_{cam} baseHcam,则有
t o o l H c a l = t o o l H b a s e i ∗ b a s e H c a m i ∗ c a m H c a l i = t o o l H b a s e j ∗ b a s e H c a m j ∗ c a m H c a l j , i ≠ j ^{tool}H_{cal}=^{tool}H_{base}^i*^{base}H_{cam}^i*^{cam}H_{cal}^i=^{tool}H_{base}^j*^{base}H_{cam}^j*^{cam}H_{cal}^j,i\neq j toolHcal=toolHbasei∗baseHcami∗camHcali=toolHbasej∗baseHcamj∗camHcalj,i=j
其中 i i i, j j j分别表示第 i i i , j j j次运动。由于 b a s e H c a m i = b a s e H c a m j ^{base}H_{cam}^i=^{base}H_{cam}^j baseHcami=baseHcamj,且始终不变,上式整理可得
( t o o l H b a s e j ) − 1 ∗ t o o l H b a s e i ∗ b a s e H c a m = b a s e H c a m ∗ c a m H c a l j ∗ ( c a m H c a l i ) − 1 , i ≠ j (^{tool}H_{base}^j)^{-1}*^{tool}H_{base}^i*^{base}H_{cam}=^{base}H_{cam}*^{cam}H_{cal}^j*(^{cam}H_{cal}^i)^{-1},i\neq j (toolHbasej)−1∗toolHbasei∗baseHcam=baseHcam∗camHcalj∗(camHcali)−1,i=j
因此有
A X = X B AX=XB AX=XB
A = t o o l H b a s e i ∗ ( t o o l H b a s e j ) − 1 , B = c a m H c a l j ∗ ( c a m H c a l i ) − 1 , X = b a s e H c a m A=^{tool}H_{base}^i*(^{tool}H_{base}^j)^{-1}, \\ B=^{cam}H_{cal}^j*(^{cam}H_{cal}^i)^{-1}, \\ X=^{base}H_{cam} A=toolHbasei∗(toolHbasej)−1,B=camHcalj∗(camHcali)−1,X=baseHcam
因此问题变为求解关于X的矩阵方程AX=XB。
求解AX=XB
求解AX=XB该问题使用Chou和Kamel方法提出的方法[1,2]。旋转部分使用四元数表示
R A R X = R X R B ⇔ q A ∗ q X = q X ∗ q B R_AR_X=R_XR_B\Leftrightarrow q_A*q_X=q_X*q_B RARX=RXRB⇔qA∗qX=qX∗qB
使用四元数乘法表示旋转变换,重新构造线性系统
q A ∗ q X − q X ∗ q B = q A ∗ q X − q B ‾ ∗ q X = ( q A − q B ‾ ) ∗ q X q_A*q_X-q_X*q_B=q_A*q_X-\overline{q_B}*q_X=(q_A-\overline{q_B})*q_X qA∗qX−qX∗qB=qA∗qX−qB∗qX=(qA−qB)∗qX
因此有
q X ∗ q B = ( x 0 − x T X ( x 0 I + S k ( x ) ) b ) ( b 0 b ) q_X*q_B=\left(\begin{matrix} x_0 & -\mathbf{x}^T \\ \mathbf{X} & ( x_0\mathbf{I}+\text{S} k(\mathbf{x}) )\mathbf{b} \end{matrix}\right) \left(\begin{matrix} b0\\ \mathbf{b} \end{matrix}\right) \\ qX∗qB=(x0X−xT(x0I+Sk(x))b)(b0b)
= ( x 0 b 0 − x T b X b 0 + ( x 0 I + S k ( x ) ) b ) =\left(\begin{matrix} x_0b_0 -\mathbf{x}^T\mathbf{b} \\ \mathbf{X}b_0 + ( x_0\mathbf{I}+\text{S} k(\mathbf{x}) )\mathbf{b} \end{matrix}\right)\\ =(x0b0−xTbXb0+(x0I+Sk(x))b)
= ( b 0 x 0 − b T x b x 0 + ( b 0 I − S k ( b ) ) x ) =\left(\begin{matrix} b_0x_0 -\mathbf{b}^T\mathbf{x} \\ \mathbf{b}x_0 + ( b_0\mathbf{I}-\text{S} k(\mathbf{b}) )\mathbf{x} \end{matrix}\right)\\ =(b0x0−bTxbx0+(b0I−Sk(b))x)
= ( b 0 − b T b ( b 0 I − S k ( b ) ) ) ( x 0 x ) = q B ‾ ∗ q X =\left(\begin{matrix} b_0 & -\mathbf{b}^T \\ \mathbf{b} & ( b_0\mathbf{I}-\text{S} k(\mathbf{b})) \end{matrix}\right) \left(\begin{matrix} x_0\\ \mathbf{x} \end{matrix}\right)\\ =\overline{q_B}*q_X =(b0b−bT(b0I−Sk(b)))(x0x)=qB∗qX
然后使用奇异值分解求解线性方程组,SVD分解实现参考第三版《Numerical Recipes》。
构建A,B矩阵时,任意两个不同位置姿矩阵,可以构造一个方程,因此输入数据的数量n与可构建方程数m的关系可以通过排列组合确定 m = C n 2 = n ( n − 1 ) / 2 m=C^2_n=n(n-1)/2 m=Cn2=n(n−1)/2。可根据此关系及标定系统能处理的最大矩阵维数,设计标定功能需要考虑系统能处理的最大输入数据量。
假设系统处理的最大矩阵维数为l,则有
l = 4 ∗ m = 4 ∗ C n 2 l=4*m=4*C^2_n l=4∗m=4∗Cn2
可得
n = ( 2 + ( 4 + 8 l ) ) / 4 n=(2+\sqrt{(4+8l)})/4 n=(2+(4+8l))/4
若输入数据量过大,可以考虑另一种方法构造A,B矩阵,使用相邻的两个位姿构建A,B矩阵。则方程数 m = n − 1 m=n-1 m=n−1,A,B矩阵的较大的维数是 4 ∗ m = 4 n − 4 4*m=4n-4 4∗m=4n−4。
仿真验证
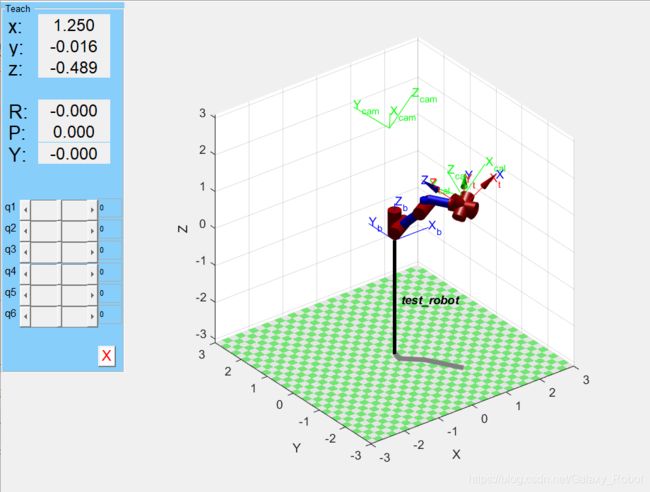
进行C++算法开发前,首先使用matlab可以较快实现,验证选定方法及推导过程的正确性。使用matlab建立随意建立一个机器人,设定好相机坐标系和标定板坐标系。然后采集不同位姿下,机器人末端在基坐标的位姿T_b_t,标定板坐标系在相机坐标系下的位姿T_c_cal。主程序如下,完整程序还包括solve_hand_eye_equation()子程序,该子程序是Chou和Kamel的方法的实现。除此外还有tsai, shiu, park, park, lu8, liang等人的方法对应的子程序tsai(), shiu(), park(), park(), lu8(), liang(),可以到这里下载【下载链接】。
%%
%eye to hand 手眼标定验证程序,以仿真验证代替物理机器验证。
%libing,2020.4.23
%%
%建立机器人模型,获得试验数据,%验证算法理论的正确性,再用于验证C++程序的正确性。
clc
clear
clc;
close('all');
%随意建立一个机器人
PM_PI=3.1415926;
deg=PM_PI/180;
% theta d a alpha sigma
ML1 = Link([ 0, 0.4967, 0, 0, 0], 'modified');
ML2 = Link([ 0, -0.18804, 0.2, 3*PM_PI/2, 0], 'modified');
ML3 = Link([ 0, 0.17248, 0.79876, 0 , 0], 'modified');
ML4 = Link([ 0, 0.98557, 0.25126, 3*PM_PI/2, 0], 'modified');
ML5 = Link([ 0, 0, 0, PM_PI/2 , 0], 'modified');
ML6 = Link([ 0, 0, 0, PM_PI/2 , 0], 'modified');
robot = SerialLink([ML1 ML2 ML3 ML4 ML5 ML6],'name','test\_robot');
robot.teach(); %可以自由拖动的关节角度
hold on;
%基坐标系
H_base=transl(0,0,0);
trplot(H_base,'frame','b','color','b');
hold on;
%axis([-2,2,-2,2,-1,3]);
%末端坐标系
T_b_t=zeros(4,4);
theta=[0,0,0,0,0,0];
T_b_t(:,1:4)=robot.fkine(theta);
fig_tool=trplot(T_b_t,'frame','t','color','b');
%设置相机坐标系(随意设置,与标定结果对比)
H_b_c=zeros(4,4);
t=transl(1,1.5,2);
H_b_c=t*trotx(15)*troty(30)*trotz(45);
fprintf("设置相机位姿为\n");
disp(H_b_c);
trplot(H_b_c,'frame','cam','color','g');
%设置机器人末端坐标系到标定板坐标系的变换(随意设置)
H_t_cal=zeros(4,4);
t=transl(0.1,0.2,0.1);
H_t_cal=t*trotx(15)*troty(30)*trotz(45);
T_b_cal=T_b_t*H_t_cal;
fig_cal=trplot(T_b_cal,'frame','cal','color','g');
%采集手眼标定所需的数据数据(10个位姿)
fp1=fopen('testq_T_b_t.txt','w');
fp2=fopen('testq_T_c_cal.txt','w');
for i=1:10
J1=-6*i*deg;
J2=-4.5*i*deg;
J3=-4.5*i*deg;
J4=3.0*i*deg;
J5=4.5*i*deg;
J6=3.0*i*deg;
theta=[J1,J2,J3,J4,J5,J6];
%采集手眼标定数据数据
T_b_t(:,4*i-3:4*i)=robot.fkine(theta); %基座坐标系到机器人末端坐标系的变换
T_b_cal=T_b_t(:,4*i-3:4*i)*H_t_cal;
%由T_b_cal=T_b_c*T_c_cal导出T_c_cal
T_c_cal(:,4*i-3:4*i)=inv(H_b_c)*T_b_cal;%相机坐标系到标定板坐标系的变换
q1(1:3)= T_b_t(1:3,4*i);%写入,用于C++程序测试
q1(4:7)=rot2q(T_b_t(1:3,4*i-3:4*i-1));
q2(1:3)= T_c_cal(1:3,4*i);%写入,用于C++程序测试
q2(4:7)=rot2q(T_c_cal(1:3,4*i-3:4*i-1));
fprintf(fp1,'%.6f %.6f %.6f %.6f %.6f %.6f %.6f\n',...
q1(1),q1(2),q1(3),q1(4),q1(5),q1(6),q1(7));
fprintf(fp2,'%.6f %.6f %.6f %.6f %.6f %.6f %.6f\n',...
q2(1),q2(2),q2(3),q2(4),q2(5),q2(6),q2(7));
pause(0.2);
delete(fig_tool);
delete(fig_cal);
fig_tool=trplot(T_b_t(:,4*i-3:4*i),'frame','t','color','r');%绘制末端坐标系
fig_cal=trplot(T_b_cal,'frame','cal','color','g');%绘制标定板坐标系
robot.plot(theta);
end
fclose(fp1);
fclose(fp2);
%利用采集的数据构造方程的系数矩阵A,B
H_b_t=T_b_t;
H_c_cal=T_c_cal;
[m,n]=size(H_b_t);
m=n/4;
fp1=fopen('testA.txt','w');
fp2=fopen('testB.txt','w');
n=1;
for i=1:m-1
j=i+1;
A(:,4*i-3:4*i)=H_b_t(:,4*j-3:4*j)*inv(H_b_t(:,4*i-3:4*i));
B(:,4*i-3:4*i)=H_c_cal(:,4*j-3:4*j)*inv(H_c_cal(:,4*i-3:4*i));
testA(4*i-3:4*i,:)=A(:,4*i-3:4*i);%用于C++程序测试
testB(4*i-3:4*i,:)=B(:,4*i-3:4*i);%用于C++程序测试
for k=1:4
fprintf(fp1,'%.6f %.6f %.6f %.6f\n',...
testA(4*i-4+k,1),testA(4*i-4+k,2),...
testA(4*i-4+k,3),testA(4*i-4+k,4));
fprintf(fp2,'%.6f %.6f %.6f %.6f\n',...
testB(4*i-4+k,1),testB(4*i-4+k,2),...
testB(4*i-4+k,3),testB(4*i-4+k,4));
end
end
fclose(fp1);
fclose(fp2);
%求AX=XB解方程
fprintf("标定结果\n");
X1=solve_hand_eye_equation(A,B);
%文献的其他方法
X2=tsai(A,B)
X3=shiu(A,B)
X4=park(A,B)
X5=lu8(A,B)
X6=liang(A,B)
matlab设置相机坐标系的相对于基坐标系位姿为
H_b_c=zeros(4,4);
t=transl(1,1.5,2);
H_b_c=t*trotx(15)*troty(30)*trotz(45);
计算得到对应的位姿为如下,这将与算法计算的结果进行对比。
H_b_c =
0.6124 -0.6124 0.5000 1.0000
0.7745 0.5915 -0.2241 1.5000
-0.1585 0.5245 0.8365 2.0000
0 0 0 1.0000
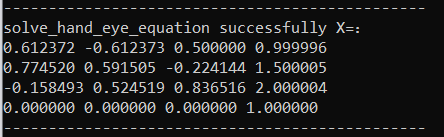
采集10组位姿数据,测试算法。计算结果如下,与设置的数据一致,验证了算法的正确性。
设置相机位姿为
0.6124 -0.6124 0.5000 1.0000
0.7745 0.5915 -0.2241 1.5000
-0.1585 0.5245 0.8365 2.0000
0 0 0 1.0000
标定结果
X2 =
0.6124 -0.6124 0.5000 1.0000
0.7745 0.5915 -0.2241 1.5000
-0.1585 0.5245 0.8365 2.0000
0 0 0 1.0000
X3 =
0.6124 -0.6124 0.5000 1.0000
0.7745 0.5915 -0.2241 1.5000
-0.1585 0.5245 0.8365 2.0000
0 0 0 1.0000
X4 =
0.6124 -0.6124 0.5000 1.0000
0.7745 0.5915 -0.2241 1.5000
-0.1585 0.5245 0.8365 2.0000
0 0 0 1.0000
X5 =
0.6124 -0.6124 0.5000 1.0000
0.7745 0.5915 -0.2241 1.5000
-0.1585 0.5245 0.8365 2.0000
0 0 0 1.0000
X6 =
0.6124 -0.6124 0.5000 1.0000
0.7745 0.5915 -0.2241 1.5000
-0.1585 0.5245 0.8365 2.0000
0 0 0 1.0000
同时采集T_b_t,T_c_cal,testA,testB的数据,用于C++程序调试和验证。
matlab程序参见solve_hand_eye_equation.m,test_robot.m。
C++程序开发
首先实现公用接口solve_hand_eye_equation(),求解AX=XB,该接口与机器人无关,作为一个通用函数。
使用matlab采集testA,testB的数据验证。运行该功能的测试用例函数test_solve_hand_eye_equation(),结果如下
其次构造一个robot类,仅包含手眼标定功能,获取相机坐标系功能,以及相机坐标系参数。
class robot {
public:
robot() = default;//默认构造函数
robot(const robot& newRobot);//复制构造函数,方便创建新机器人
int hand_eye_calibarate(int num, double T_b_t[][7], double T_c_cal[][7]);
void get_hand_eye_param(double T[4][4]);
private:
double H_b_c[4][4] = { {0} };//基坐标系到相机固定坐标系的齐次变换
//double DHparam[6][5];机器人DH参数
protected:
};
最后实现手眼标定接口,接口主要实现把输入数据的四元数形式转换为旋转矩阵,构造A,B矩阵,最后调用solve_hand_eye_equation()求解方程AX=XB。运行该功能的测试用例函数hand_eye_calibarate() 结果如下,与matlab仿真验证的结果一致(使用matlab机器人模型采集的数据),算法验证完成。
T_b_t:
1.389353 -0.161673 -0.374760 -0.000012 -0.039367 -0.052134 0.997864
1.495724 -0.333834 -0.238036 -0.000190 -0.079298 -0.102923 0.991523
1.562537 -0.524060 -0.080913 -0.000948 -0.120277 -0.151058 0.981180
1.585289 -0.722849 0.093874 -0.002944 -0.162627 -0.195301 0.967161
1.561916 -0.919740 0.283137 -0.007023 -0.206449 -0.234523 0.949910
1.492980 -1.103947 0.483300 -0.014154 -0.251564 -0.267729 0.929966
1.381702 -1.265028 0.690486 -0.025352 -0.297486 -0.294087 0.907949
1.233814 -1.393543 0.900604 -0.041587 -0.343405 -0.312952 0.884537
1.057254 -1.481657 1.109443 -0.063695 -0.388197 -0.323880 0.860435
0.861714 -1.523652 1.312769 -0.092296 -0.430459 -0.326641 0.836356
T_c_cal:
-0.474389 -2.366986 -1.315044 -0.022235 -0.050624 -0.034793 0.997864
-0.569053 -2.470300 -1.093639 -0.045221 -0.100774 -0.068418 0.991523
-0.707189 -2.547185 -0.871851 -0.069796 -0.149797 -0.099877 0.981180
-0.883184 -2.590179 -0.657082 -0.096807 -0.196832 -0.128393 0.967161
-1.088846 -2.593220 -0.456094 -0.127029 -0.240827 -0.153420 0.949910
-1.313870 -2.552169 -0.274656 -0.161076 -0.280563 -0.174650 0.929966
-1.546457 -2.465225 -0.117259 -0.199323 -0.314694 -0.192005 0.907949
-1.774056 -2.333193 0.013063 -0.241839 -0.341809 -0.205610 0.884537
-1.984178 -2.159575 0.114821 -0.288338 -0.360497 -0.215766 0.860435
-2.165222 -1.950474 0.188031 -0.338148 -0.369429 -0.222904 0.836356
------------------标定前Tcam:----------------
0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.000000 0.000000
------------------标定后Tcam:----------------
0.612370 -0.612373 0.500003 0.999996
0.774521 0.591504 -0.224143 1.499992
-0.158495 0.524521 0.836515 1.999987
0.000000 0.000000 0.000000 1.000000
小结
(1)不管是eye-to-hand系统,还是eye-in-hand系统,问题的关键都是转化为求解方程AX=XB。
(2)本文的所述方法不适用于scara机器人,这类方法可以得出唯一解的充分条件是至少有两次机械臂运动的旋转轴是非平行的。
(3)这里的仿真数据没有加入噪声,所以各种方法的计算结果都是一样的。实际应用中各种方法的结果应该是有一定差异的。
参考资料
[1]Shah, R. D. Eastman, T. Hong, An Overview of Robot-Sensor Calibration Methods for Evaluation of Perception Systems, Performance Metrics for Intelligent Systems, (2012).
[2]J. C. K. Chou, M. Kamel Finding the Position and Orientation of a Sensor on a Robot Manipulator Using Quaternions. In The International Journal of Robotics Research, 10(3): 240-254, 1991.
[3]R. Tsai, R. Lenz A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration. In IEEE Transactions on Robotics and Automation, 5(3):345-358, 1989.
[4]程玉立. 面向工业应用的机器人手眼标定与物体定位[D].浙江大学,2016.
[5]张云珠. 工业机器人手眼标定技术研究[D].哈尔滨工程大学,2010.
r on a Robot Manipulator Using Quaternions. In The International Journal of Robotics Research, 10(3): 240-254, 1991.
[3]R. Tsai, R. Lenz A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration. In IEEE Transactions on Robotics and Automation, 5(3):345-358, 1989.
[4]程玉立. 面向工业应用的机器人手眼标定与物体定位[D].浙江大学,2016.
[5]张云珠. 工业机器人手眼标定技术研究[D].哈尔滨工程大学,2010.
[6]William H. Press, Saul A. Teukolsky. Numerical Recipes: The Art of Scientific Computing (3rd Edition)