深度学习基础 - 前向传播和反向传播

深度学习基础 - 前向传播和反向传播

flyfish

有一个故事：
一位外地人闯进小镇，到镇里的旅店，取出100元钱准备住店，然后便随服务员去看房。旅店老板拿着这100元钱到街对面的肉铺还赊账买肉的钱；肉铺老板赶紧跑去一公里外的养猪场还了买猪钱；养猪场场主开开心心地将还没捂热的100元钱又还给前来催债的邻镇饲料厂厂长；厂长正惦记着前几天住旅店欠下的100元钱，飞奔到旅店将钱还上。外地人向旅店老板反映房间环境不好，要退掉100元房钱，老板便将饲料厂厂长付给自己的钱给了这个外地人。这下子，小镇上的人债务都解除了，大家都很开心。

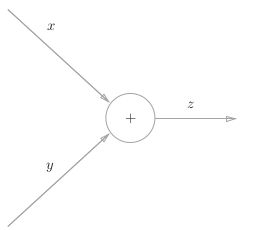
从一个简单的数学表达式开始
$$1+2=3$$
把常量换成变量，如下
$$x+y=z$$
这是数学表达式的方式

我们再换种计算图的方式，如下

前向传播

反向传播
这是加法，左边是前向传播，右边是反向传播

这是乘法，左边是前向传播，右边是反向传播

从左向右进行计算是一种正方向上的传播,简称为正向传播 (forward propagation)。从右向左的传播称为反向传播 (backward propagation)。
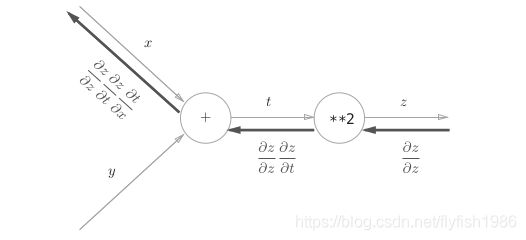
计算图的反向传播
计算图的反向传播:沿着与正方向相反的方向,乘上局部导数。
反向传播的计算顺序是：
将信号 E 乘以节点的局部导数( $\frac{\partial y}{\partial x}$),然后将结果传递给下一个节点。这里所说的局部导数是指正向传播中$y=f(x)$ 的导数,也就是 y 关于 x 的导数( $\frac{\partial y}{\partial x}$ )。比如,假设 $y=f(x)=x2$ ,则局部导数为$\frac{\partial y}{\partial x}$ = 2x。把这个局部导数乘以 E,然后传递给前面的节点。这就是反向传播的计算顺序。通过这样的计算,可以高效地求出导数的值,这是反向传播的要点。

$z=f(x,y)$ 求偏导数
加法的偏导数
$$\begin{array}{l}f(x,y)=x+y\\ \\ \frac{\partial f}{\partial x}=1,\\ \\ \frac{\partial f}{\partial y}=1\end{array}$$
乘法的偏导数

$$\begin{array}{l}f(x,y)=xy\\ \\ \frac{\partial f}{\partial x}=y,\\ \\ \frac{\partial f}{\partial y}=x\end{array}$$

我们把加法和乘法联合起来，以应用题的方式说明正向传播和反向传播
完整代码
物品a的单价是3,数量是7
物品b的单价是4,数量是8
物品的总价是多少？
3×7 + 4×8 = 53
代码实现

class multiplication_layer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y
        return out

    def backward(self, d_out):
        d_x = d_out * self.y
        d_y = d_out * self.x
        return d_x, d_y


class addition_layer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y
        return out

    def backward(self, d_out):
        d_x = d_out * 1
        d_y = d_out * 1
        return d_x, d_y

a_price = 3
a_num = 7
b_price = 4
b_num = 8


# layer
a_layer = multiplication_layer()
b_layer = multiplication_layer()
c_layer = addition_layer()

# forward
a_price = a_layer.forward(a_price, a_num)  # (1)
b_price = b_layer.forward(b_price, b_num)  # (2)
totoal_price = c_layer.forward(a_price, b_price)  # (3)

# backward
d_price = 1
d_a_price, d_b_price = c_layer.backward(d_price)  # (3)
d_b, d_b_num = b_layer.backward(d_b_price)  # (2)
d_a, d_a_num = a_layer.backward(d_a_price)  # (1)

print("totoal_price:", (totoal_price))
print("d_a:", d_a)
print("d_a_num:", (d_a_num))
print("d_b:", d_b)
print("d_b_num:", (d_b_num))

# totoal_price: 53
# d_a: 7
# d_a_num: 3
# d_b: 8
# d_b_num: 4

局部计算 - 各人自扫门前雪，莫管他人瓦上霜
计算图的特征是可以通过传递“局部计算”获得最终结果。通过一个乘号看局部计算是指,无论全局发生了什么,这个乘号只根据与自己相关两个连接的信息计算与其他点和线无关。
在计算图中表示链式法则

$$z={(x+y)}^2$$是由两个式子构成的。
$$1、z=t^{2}2、t=x+y$$

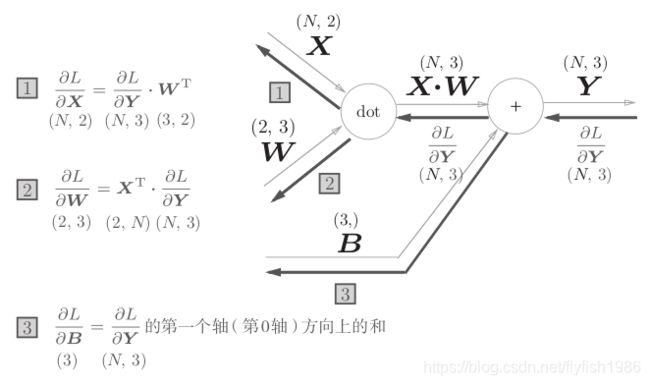
简单实现一个全连接层的前向传播和反向传播
全连接层是fully connected layer，类似的名词是affine或者linear

$$Y=WX+B$$

import numpy as np
N=1
X= np.random.random((N,2))
W= np.random.random((2,3))
B= np.random.random((3,))
Y = np.dot(X, W) + B
print(Y)

以矩阵为对象的反向传播
$$\begin{array}{l}\frac{\partial L}{\partial \mathbf{X}}=\frac{\partial L}{\partial \mathbf{Y}}\cdot {\mathbf{W}}^{\mathrm{T}}\\ \\ \frac{\partial L}{\partial \mathbf{W}}={\mathbf{X}}^{\mathrm{T}}\cdot \frac{\partial L}{\partial \mathbf{Y}}\end{array}$$
X 和 $\frac{\partial L}{\partial X}$形状相同,W 和 $\frac{\partial L}{\partial W}$形状相同
$$\begin{array}{l}\mathbf{X}=\left(x_0,x_1,\cdots ,x_n\right)\\ \frac{\partial L}{\partial \mathbf{X}}=\left(\frac{\partial L}{\partial x_0},\frac{\partial L}{\partial x_1},\cdots ,\frac{\partial L}{\partial x_n}\right)\end{array}$$

转置操作会把 W 的元素 (i, j) 换成元素
(j, i)。用数学式表示的话
$$\begin{array}{rl}\mathbf{W}& =\left(\begin{array}{lll}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\end{array}\right)\end{array}$$
$$\begin{array}{r}{\mathbf{W}}^{\mathrm{T}}=\left(\begin{array}{ll}{w}_{11}& w_{21}\\ w_{12}& w_{22}\\ w_{13}& w_{23}\end{array}\right)\end{array}$$

import numpy as np

class fully_connected_layer:
    def __init__(self,W, B):
        self.X = None
        self.W = W
        self.B = B
        self.dx = None
        self.dw = None
        self.db = None

    def forward(self, input):
        self.X = input
        out = np.dot(self.X, self.W) + self.B
        return out

    def backward(self, d_out):
        self.dx = np.dot(d_out, self.W.T)
        self.dw = np.dot(self.X.T,d_out)
        self.db = np.sum(d_out, axis=0)
        return self.dx

np.random.seed(2020)

N=2
input= np.random.random((N,2))
weight= np.random.random((2,3))
bias= np.random.random((3,))

print(input.shape)
print("input=\n",input)

print(weight.shape)
print("weight=\n",weight)

print(bias.shape)
print("bias=\n",bias)

linear = fully_connected_layer(W=weight,B=bias)

out = linear.forward(input)
print("out=\n",out)

d_out= np.random.random(out.shape)
dx = linear.backward(d_out)
dw = linear.dw
db = linear.db
print("dx=\n",dx)
print("dw=\n",dw)
print("db=\n",db)

计算的都是偏导数为什么说是梯度呢？ （参考文档）
反向传播（Backpropagation，缩写为BP）是“误差反向传播”的简称，该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给梯度下降法，用来更新权值以最小化损失函数。

这个算法的名称意味着误差会从输出结点反向传播到输入结点。

给定函数$f(x)$ ，其中$x$是输入向量，需要计算函数$f$关于$x$的梯度，也就是$\nabla f(x)$。
梯度$\nabla f$是偏导数的向量，所以我们有 $\nabla f=[\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}]=[y,x]$。
尽管从技术上讲，梯度是一个向量。为简单起见，我们经常使用诸如“$x$上的梯度（the gradient on x）”之类的术语来代替技术上正确的短语“$x$上的偏导数（the partial derivative on $x$）”。

上面的描述中未加激活函数，这里的非线性函数就是激活函数 （下图省了偏置）

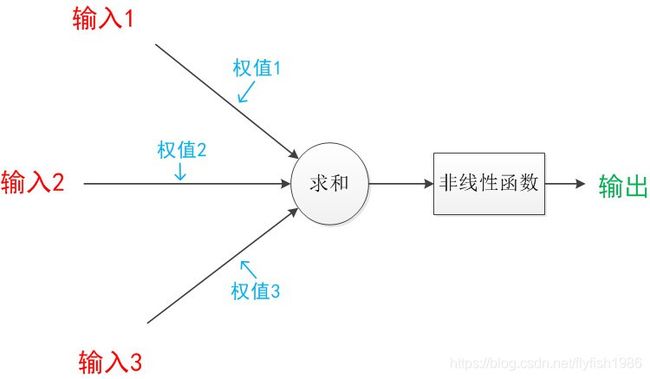
变成符号通常是这样 （下图b就是偏置）

有的资料是把累加计算和激活函数都放到一个圈中

把上面的式子拆解就是
$$\begin{gathered} x_1\to x_1\ast w_1 \\ {x}_2\to x_1\ast w_2 \\ {x}_3\to x_1\ast w_3 \end{gathered}$$
加权的输入加在一起得到z，然后通过激活函数得到a
$$\begin{gathered} z=x_1\ast w_1+x_2\ast w_2+x_3\ast w_3+b \\ a=f(z) \end{gathered}$$

下图展示关于权重的通常表示方法

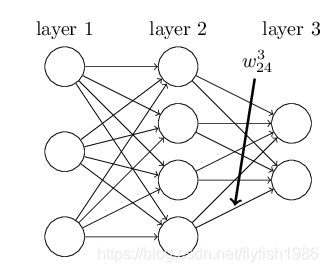
上图$w_{jk}^l$ 显示的是从网络第二层的第四个神经元到第三层的第二个神经元的连接的权重：

简单写是
$$\begin{array}{l}{a}^l=\sigma (w^l{a}^{l-1}+b^l).\end{array}$$
详细写是
$$\begin{array}{l}{a}_j^l=\sigma ({\sum }_k{w}_{jk}^l{a}_k^{l-1}+b_j^l)\end{array}$$

$w_{jk}^l$ 为什么这样表示呢？ 这样表示也是有原因的(参考文档)
它的一个奇怪之处是$j$和$k$ 的顺序。你可能认为更合理的操作是：使用 j表示输入神经元、 k表示输出神经元，反之就不成立了，是这样。下面将解释这个奇怪现象的原因。
答案如下：
我们使用类似的符号来表示网络的偏置和激活结果。
$b_j^l$表示$l^{th}$层中的 $j^{th}$神经元的偏差；
用 $a_j^l$来表示激活$l^{th}$ 层中的$j^{th}$ 神经元。下面的图表展示了这些符号的应用

有了这些符号，$l^{th}$ 层中的 $j^{th}$ 神经元的激活 $a_j^l$ 与 $(l-1{)}^{th}$ 层中的激活产生了关联，公式如下：
$$a_j^l=\sigma (\sum _k{w}_{jk}^l{a}_k^{l-1}+b_j^l)\text{\hspace{1em}(23)}$$
其中，求和表示的是 $(l-1{)}^{th}$ 层中所有神经元共计 $k$ 个。为了以矩阵形式重写这个表达式，我们为每个层 $l$ 定义一个权重矩阵 $w^l$，权重矩阵 $w^l$ 的各项是连接到神经元的 $l^{th}$ 层的权重，也就是说，$j^{th}$ 行和 $k^{th}$ 列中的项是 $w_{jk}^l$。类似地，对于每个层 $l$，我们定义一个偏差向量，$b^l$。你也许可以猜出这样操作的原理 —— 偏差向量的元素 $b_j^l$ ，是 $l^{th}$ 层中每个神经元的一个分量。最后，我们定义了一个激活函数的输出向量 $a^l$，它的分量是 $a_j^l$。
将（23）式用矩阵形式重写，不过，这里还需要将激活函数（ $\sigma$ ）向量化。基本想法是函数（$\sigma$）应用于向量 $\mathbf{v}$ 中的每个元素，于是用符号 $\sigma (\mathbf{v})$ 来表示函数的这种应用，也就是说， $\sigma (\mathbf{v})$ 的分量只是 $\sigma (\mathbf{v}{)}_j=\sigma ({\mathbf{v}}_j)$。举个例子，对于函数 $f(x)=x^2$，$f$ 向量化形式的效果如下：

$$f\left(\left[\begin{array}{l}2\\ 3\end{array}\right]\right)=\left[\begin{array}{l}f(2)\\ f(3)\end{array}\right]=\left[\begin{array}{l}4\\ 9\end{array}\right]$$

也就是说，向量化的 $f$ 只是对向量的每个元素求平方。
有了这些符号，我们就可以把式（23）改写成漂亮而紧凑的向量化形式：
$$a^l=\sigma (w^l{a}^{l-1}+b^l)\text{\hspace{1em}(25)}$$
这个表达式使我们可以从全局的角度来思考问题：一个层里的激活函数是如何与前一层里的激活输出相关联的。我们只需将权重矩阵应用于激活函数，然后添加偏置向量，最后应用 $\sigma$ 函数（顺便说一下，正是这个表达式激活了前面提到的 $w_{jk}^l$ 符号中的怪现象。如果我们用 $j$ 来表示输入的神经元，用 $k$ 来表示输出的神经元，那么，我们需要用权重矩阵的转置来代替方程（25）中的权重矩阵。这是一个很小的改变，但是很烦人，我们将失去简单易懂的说法（和想法）：“将权重矩阵应用于激活函数”。与我们现在所采用的逐神经元观点相比，这种全局观点通常更简单、更简洁（涉及的指数更少！）。这种方法可以使我们逃离“角标地狱”，同时仍然精确地表述所发生的情况。该表达式在实践中也很有用，因为大多数矩阵库提供了实现矩阵乘法、向量加法和向量化的快速方法。
当使用方程（25）计算 $a^l$ 时，我们计算中间量 $z^l=w^l{a}^{l-1}+b^l$。把 $z^l$ 称为层 $l$ 中的神经元的加权输入。我们将在后半部分大量使用加权输入 $z^l$。方程(25) 有时用加权输入来表示，如：$a^l=\sigma (z^l)$。同样值得注意的是，$z^l$ 包含 $z_j^l={\sum }_k{w}_{jk}^l{a}_k^{l-1}+b_j^l$，也就是说，$z_j^l$ 只是层 $l$ 中神经元 $j$ 的激活函数的加权输入。

量化网络是否能够做得“更好”，那就是损失函数（loss）。

这里，我们将使用损失函数的一种——均方误差来计算。
$$\text{MSE}=\frac{1}{n}\sum _{i=1}^n(y_{true}-y_{pred}{)}^2$$

$(y_{true}-y_{pred}{)}^2$ 被称为平方误差。

类似损失函数写为多变量函数如下 w和b都少一少
$$Loss(w_1,w_2,w_3,b_1)$$
我们只要调整w1，就可能导致Loss的变化
$$\frac{\partial Loss}{\partial w_1}=\frac{\partial Loss}{\partial y_{pred}}\ast \frac{\partial y_{pred}}{\partial w_1}$$

我们说反向传播是对网络中所有权重计算损失函数的梯度。这个梯度会反馈给梯度下降法，用来更新权值以最小化损失函数。
用式子可视化下，你会疑惑 怎么是公式呢？因为我看下面的公式就看几何图像一样。

看梯度，梯度是一个向量，里面装着很多偏导数
这个梯度计算之后，再把梯度自己给梯度下降用。
展示梯度:
$$\nabla L={\left[\begin{array}{c}\frac{\partial L}{\partial w_0}\\ \\ \frac{\partial L}{\partial w_1}\\ \\ \frac{\partial L}{\partial w_2}\\ \\ ...\\ \\ \frac{\partial L}{\partial w_j}\\ \\ ...\\ \\ \frac{\partial L}{\partial b}\end{array}\right]}_{gradient}$$
展示梯度下降的重要过程,我们看梯度就在其中。
$$gradientdescent:{\left[\begin{array}{c}{w}_0^{\prime }\\ w_1^{\prime }\\ w_2^{\prime }\\ ...\\ w_j^{\prime }\\ ...\\ b^{\prime }\end{array}\right]}_{L=L^{\prime }}={\left[\begin{array}{c}{w}_0\\ w_1\\ w_2\\ ...\\ w_j\\ ...\\ b\end{array}\right]}_{L=L_0}-\eta {\left[\begin{array}{c}\frac{\partial L}{\partial w_0}\\ \frac{\partial L}{\partial w_1}\\ \frac{\partial L}{\partial w_2}\\ ...\\ \frac{\partial L}{\partial w_j}\\ ...\\ \frac{\partial L}{\partial b}\end{array}\right]}_{L=L_0}$$
参考
How the backpropagation algorithm works
CS231n Convolutional Neural Networks for Visual Recognition
《深度学习入门》
《深度学习》