常见激活函数适用场景及优缺点分析

什么是激活函数

激活函数（Activation Function）是一种添加到人工神经网络中的函数，旨在帮助网络学习数据中的复杂模式。在神经元中，输入的input经过一系列加权求和后作用于另一个函数，这个函数就是这里的激活函数。下图为单个感知机模型的结构，其中$f(\cdot )$即为激活函数，$y=f(\sum w_i{x}_i)$。

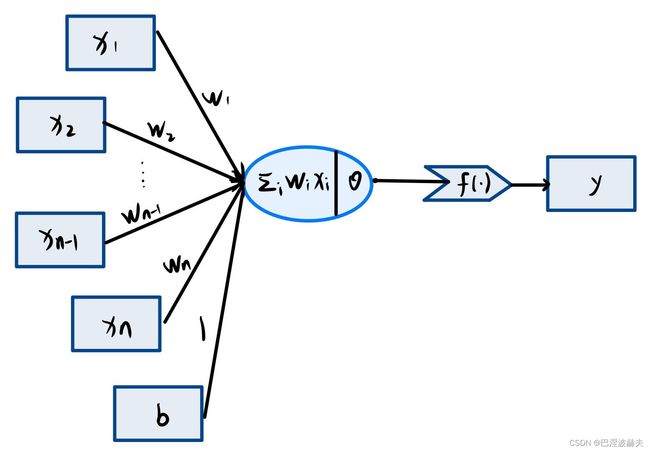
激活函数的作用

对于一个多层感知机，给当一个小批量样本$X\in {\mathbb{R}}^{n\times d}$，其批量大小为$n$，输入个数为$d$。假设多层感知机只有一个隐藏层，其中隐藏单元个数为$h$。记隐藏层的输出（也成为隐藏层变量或隐藏变量）为$H$，有$H\in \mathbb{R}d\times h$。因为隐藏层和输出层军事全连接层，可以设隐藏层的权重参数和偏差参数分别为$W_h\in {\mathbb{R}}^{d\times h}$和$b_h\in \mathbb{R}1\times h$，输出层的权重和偏差参数分别为$W_o\in \mathbb{R}h\times q$和$b_o\in \mathbb{R}1\times q$。

不妨设一种含但隐藏层的多层感知机的设计。其输出$O\in \mathbb{R}n\times q$的计算为$$H=X{W}_h+b_h$$$$O=H{W}_o+b_o$$

也就是将隐藏层的输出直接作为输入层的输入。如果将以上两个式子连立起来，可以得到$$O=(X{W}_h+b_h)W_o+b_o=X{W}_h{W}_o+b_h{W}_o+b_o$$

从联立后的狮子可以看出，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络：其中输出层权重参数为$W_h{W}_o$，偏差参数为$b_h{W}_o+b_o$。不难发现，即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价。

该问题的根源在于全连接层只是对数据做仿射变换（affine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算得非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数（activation function）。

激活函数的特性

可微性：但优化方法是基于梯度的时候，这个性质是必需的，否则无法进行反向传播。

单调性：当激活函数是单调的时候，单层神经网络能保证是凸函数。

输出值的范围：当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限的时候，模型的训练会更加高效，不过这种情况下，一般需要更小的学习率（learning rate）。

从目前来看，常见的激活函数多是分段线性和具有指数形状的非线性函数。

常用激活函数

sigmoid

$$f(x)=\frac{1}{1+e^{-x}}$$

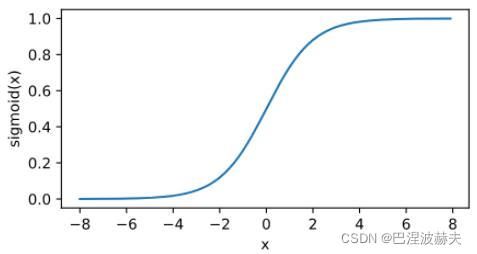
sigmoid函数在早期的神经网络中较为普遍，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。不过它目前逐渐被更简单的ReLU函数取代。

适用情况：

1.Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到1，因此它对每个神经元的输出进行了归一化；

2.用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1，因此 Sigmoid 函数非常合适；

3.梯度平滑，避免「跳跃」的输出值；

4.函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率；

5.明确的预测，即非常接近 1 或 0。

缺点：

在讲sigmoid的缺点前，我们先了解一下饱和性的概念：

当我们的n趋近于正无穷，激活函数的导数趋近于0，那么我们称之为右饱和；当我们的n趋近于负无穷，激活函数的导数趋近于0，那么我们称之为左饱和；当一个函数既满足左饱和又满足右饱和的时候我们就称之为饱和。

对于任意的x，如果存在常数c，当x>c时，恒有$f^{\prime }(x)=0$则称其为右硬饱和；如果对于任意的x，如果存在常数c，当x$f^{\prime }(x)=0$,则称其为左硬饱和；既满足左硬饱和又满足右硬饱和的我们称这种函数为硬饱和。

对于任意的x，如果存在常数c，当x>c时，恒有$f^{\prime }(x)$趋近于零，则称其为右软饱和；对于任意的x，如果存在常数c，当x$f^{\prime }(x)$趋近于零，则称其为右软饱和；既满足左软饱和又满足右软饱和的我们称这种函数为软饱和。

1.梯度消失：sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。具体来说，由于在后向传递过程中，sigmoid向下传导的梯度包含了一个 f′(x)f′(x) 因子（sigmoid关于输入的导数），因此一旦输入落入饱和区，f′(x)f′(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象

2.不以零为中心：Sigmoid 输出不以零为中心的,，输出恒大于0，非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移（Bias Shift），并进一步使得梯度下降的收敛速度变慢。

3.计算成本高昂：exp() 函数与其他非线性激活函数相比，计算成本高昂，计算机运行起来速度较慢。

tanh

$$f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$$

tanh可变形为：$$tanh(x)=2sigmoid(2x)-1$$

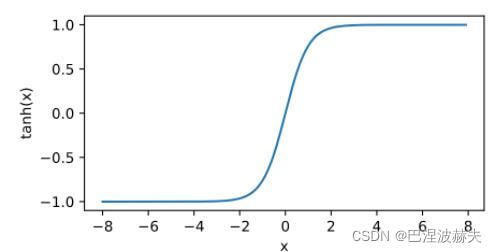
tanh也是一种非常常见的激活函数，亦称双曲正切激活函数。与 Sigmoid 函数类似，Tanh 函数也使用真值，但 Tanh 函数将其压缩至-1 到 1 的区间内。与 Sigmoid 不同，Tanh 函数的输出以零为中心，因为区间在-1 到 1 之间。在一般的二元分类问题中，tanh 函数用于隐藏层，而 sigmoid 函数用于输出层，但这并不是固定的，需要根据特定问题进行调整。

优点：

1.与sigmoid相比，它的输出均值是0，使得其收敛速度要比sigmoid快，减少迭代次数。

2.负数输入被当作负值，零输入值的映射接近零，正数输入被当作正值。

3.在实践中，Tanh 函数的使用优先性高于 Sigmoid 函数。

缺点：

tanh一样具有软饱和性，从而造成梯度消失，在两边一样有趋近于０的情况。

ReLU

$$f(x)=max(0,x)$$

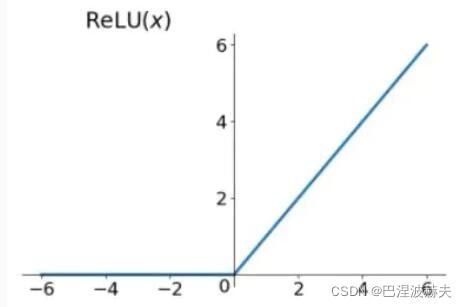
ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题，在目前的深度神经网络中被广泛使用。 可以看到，当x<0时，ReLU硬饱和，而当x>0时，则不存在饱和问题。所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。这让我们能够直接以监督的方式训练深度神经网络，而无需依赖无监督的逐层预训练。

优点:

1.当输入为正时，导数为1，一定程度上改善了梯度消失问题，加速梯度下降的收敛速度；

2.计算速度快得多。ReLU 函数中只存在线性关系，因此它的计算速度比 sigmoid 和 tanh 更快。

3.被认为具有生物学合理性（Biological Plausibility）,比如单侧抑制、宽兴奋边界（即兴奋程度可以非常高）

缺点：

1.Dead ReLU 问题：ReLU神经元在训练时比较容易“死亡”。在训练时，如果参数在一次不恰当的更新后，第一个隐藏层中的某个ReLU 神经元在所有的训练数据上都不能被激活，那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远不能被激活。这种现象称为死亡ReLU问题，并且也有可能会发生在其他隐藏层。因此当输入为负时，ReLU 完全失效，在正向传播过程中，这不是问题。有些区域很敏感，有些则不敏感。但是在反向传播过程中，如果输入负数，则梯度将完全为零。如果 learning rate 很大，那么很有可能网络中的 40% 的神经元都”dead”了。

2.不以零为中心：和 Sigmoid 激活函数类似，ReLU 函数的输出不以零为中心，ReLU 函数的输出为 0 或正数,给后一层的神经网络引入偏置偏移，会影响梯度下降的效率。

P-ReLU与 Leaky-ReLU
针对在x<0的硬饱和问题，我们对ReLU做出相应的改进:
$$L(Y,f(X))=\{\begin{array}{ll}x,& \text{if x≥0}\\ ax,& \text{if x<0}\end{array}$$

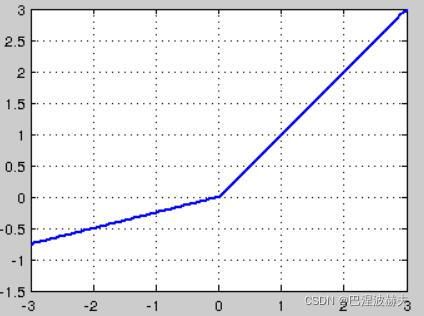
这就是Leaky-ReLU, 而P-ReLU认为，α也可以作为一个参数来学习，原文献建议初始化a为0.25，不采用正则。

为什么使用Leaky ReLU会比ReLU效果要好

1.Leaky ReLU 通过把 x 的非常小的线性分量给予负输入（0.01x）来调整负值的零梯度（zero gradients）问题，当 x < 0 时，它得到 0.1 的正梯度。该函数一定程度上缓解了 dead ReLU 问题，

2.leak 有助于扩大 ReLU 函数的范围，通常 a 的值为 0.01 左右；

3.Leaky ReLU 的函数范围是（负无穷到正无穷）

注意：尽管Leaky ReLU具备 ReLU 激活函数的所有特征（如计算高效、快速收敛、在正区域内不会饱和），但并不能完全证明在实际操作中Leaky ReLU 总是比 ReLU 更好。在很多情况下，最好使用 ReLU，但是你可以使用 Leaky ReLU 或 Parametric ReLU 进行实践，看看哪一种方式是否更适合你的问题。

ELU

$$L(Y,f(X))=\{\begin{array}{ll}x,& \text{if x≥0}\\ \alpha (e^x-1),& \text{if x<0}\end{array}$$

ELU（Exponential Linear Unit） 的提出同样也是针对解决 ReLU负数部分存在的问题，由Djork等人提出,被证实有较高的噪声鲁棒性,左侧具有软饱和性，右侧无饱和性。ELU激活函数对 小于零的情况采用类似指数计算的方式进行输出。与 ReLU 相比，ELU 有负值，这会使激活的平均值接近零。均值激活接近于零可以使学习更快，因为它们使梯度更接近自然梯度。
在ImageNet上，不加 Batch Normalization 30 层以上的 ReLU 网络会无法收敛，PReLU网络在MSRA的Fan-in （caffe ）初始化下会发散，而 ELU 网络在Fan-in/Fan-out下都能收敛。

优点

显然，ELU 具有 ReLU 的所有优点，且

1.没有 Dead ReLU 问题，输出的平均值接近 0，以 0 为中心；

2.ELU 通过减少偏置偏移的影响，使正常梯度更接近于单位自然梯度，从而使均值向零加速学习；

3.ELU 在较小的输入下会饱和至负值，从而减少前向传播的变异和信息。

缺点

一个小问题是它的计算强度更高，计算量较大。与 Leaky ReLU 类似，尽管理论上比 ReLU 要好，但目前在实践中没有充分的证据表明 ELU 总是比 ReLU 好。

softmax

$$S_i=\frac{e^i}{{\sum }_j{e}^j}$$

Softmax 是用于多类分类问题的激活函数，在多类分类问题中，超过两个类标签则需要类成员关系。对于长度为 K 的任意实向量，Softmax 可以将其压缩为长度为 K，值在（0，1）范围内，并且向量中元素的总和为 1 的实向量。

优点：

Softmax 与正常的 max 函数不同：max 函数仅输出最大值，但 Softmax 确保较小的值具有较小的概率，并且不会直接丢弃。我们可以认为它是 argmax 函数的概率版本或「soft」版本。

Softmax 函数的分母结合了原始输出值的所有因子，这意味着 Softmax 函数获得的各种概率彼此相关。

缺点：

1.在零点不可微；

2.负输入的梯度为零，这意味着对于该区域的激活，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。

与sigmoid的区别：

Maxout

$$f(x)=max(w_1^{T}x+b_1,w_2^{T}x+b_2,\cdots ,w_n^T+b_n)$$

其本质是对所有out作max操作，又被称为大一统的激活函数，因为maxout网络能够近似任意连续函数，且当w2,b2,…,wn,bn为0时，退化为ReLU。Maxout能够缓解梯度消失，同时又规避了ReLU神经元死亡的缺点，但增加了参数和计算量。

maxout激活函数并不是一个固定的函数，不像Sigmod、Relu、Tanh等函数，是一个固定的函数方程。它是一个可学习的激活函数，因为我们 W 参数是学习变化的。Maxout单元不但是净输入到输出的非线性映射，而是整体学习输入到输出之间的非线性映射关系，可以看做任意凸函数的分段线性近似，并且在有限的点上是不可微的。

优点：

Maxout的拟合能力非常强，可以拟合任意的凸函数。Maxout具有ReLU的所有优点，线性、不饱和性。同时没有ReLU的一些缺点。如：神经元的死亡。实验结果表明Maxout与Dropout组合使用可以发挥比较好的效果。

缺点：

从上面的激活函数公式中可以看出，每个神经元中有两组(w,b)参数，那么参数量就增加了一倍，这就导致了整体参数的数量激增。