基于LSSVM和PSO进行信号预测（Matlab代码实现）

 个人主页：研学社的博客 

 

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

1 概述

LSSVM模型的本质是一个分类机,优化目标是得到最优分类间隔使得模型的拟合误差最小，在区域铁路货运量预测中，其优化目标、约束条件表示为
 

     

可以发现,LSS VM优化目标是带约束的等式，其求解仍存在难度,引入拉格朗日函数简化求解过程。通过拉格朗日函数将原始的约束问题转化为无约束问题,在高维空间内有效地运用核函数简化求解过程。
 

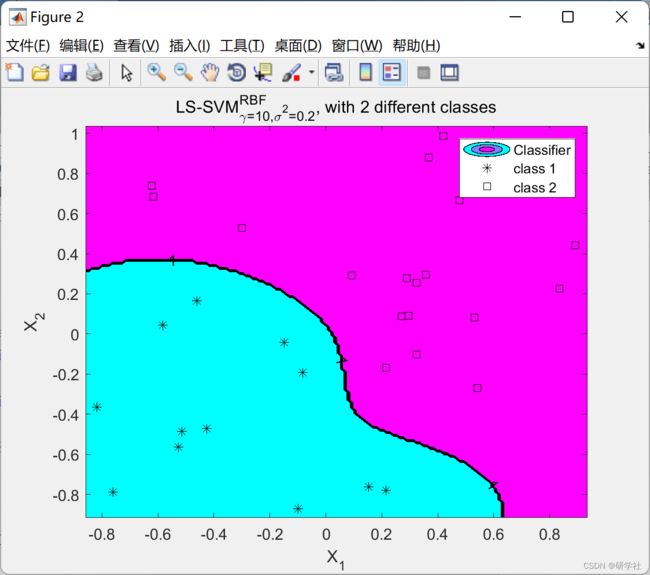
2 运行结果

 

 

部分代码：

eval('distfct;','distfct=''codedist_hamming'';');
eval('dist;','dist=2'';');
nb = ceil(log2(m*dist));
codebook =[];

candidates = eps.*ones(nb,1);
while isempty(codebook),
  disp(['number of bits ' num2str(nb)]);
  if nb>2^(m-1), error('No such code feasable'); end
  [codebook,sc] = create_code(candidates, m, dist, distfct,[]); 
  if isempty(codebook),
    nb=nb+1;
    candidates = eps.*ones(nb,1);
  else
    hd=inf;
    hdM = 0;
    for t1=1:size(codebook,1),    for t2=(t1+1):size(codebook,1),
    hd = min(hd,feval(distfct,codebook(t1,:), codebook(t2,:)));
    hdM = max(hdM,feval(distfct,codebook(t1,:), codebook(t2,:)));
    end; end

    if hd==0|hdM==size(codebook,2), 
      candidates = sc;
      codebook=[]; disp('retry'); 
    end   
  end
end

%
% output format, where 'b' stands for binary discriminator
% see also 'code' and 'codelssvm'
scheme = []; for i=1:nb, scheme = [scheme 'b']; end

function [code,shrunkcandidate,rc] = create_code(candidates, m, dist, distfct,foundcand)
%
% recursive called function
%

% base case
if isempty(candidates), code=[]; shrunkcandidate=[]; rc=0; return; end 

% pick a candidate
[nb,nc] = size(candidates);
rc=ceil(rand*nc);
acode = candidates(:,rc);

% initate this candidate
% and remove from the candidate list
acode = (acode~=eps).*acode;
aicode = acode +(acode==0).*sign(rand(nb,1)-.5);
if sum(acode==0)==0,
  candidates = candidates(:,[1:(rc-1) (rc+1):nc]);
else
  while(acode==aicode),
    aicode = acode + (acode==0).*sign(rand(nb,1));
  end
end
aicode = aicode+(aicode==0).*eps;
acode = acode+(acode==0).*eps;

candidates = shrink(candidates, aicode, dist, distfct);
shrunkcandidate = shrink(acode, aicode, dist, distfct);

% recursion
if m-1>0,
  shrunkc = candidates;
  
  fprintf('R;');
  [newcode,shrunkcandidate2,cc] = create_code(candidates,m-1, dist, distfct,[foundcand aicode]);
  fprintf('O;');
  while isempty(newcode),
    if isempty(find(shrunkcandidate2)), code=[]; return; end
    disp('retry with left candidates'); 
    shrunkc = [shrunkc(:,1:(cc-1)) shrunkcandidate2  shrunkc(:,(cc+1):end)];
    [newcode,shrunkcandidate2,cc] = create_code(shrunkc, m, dist, distfct,foundcand);
  end
  code = [aicode newcode];
 else
  code = aicode;
end

shrunkcandidate = candidates;

function shrunkcandidates = shrinkr(candidates, aicode, dist, distfct)
% refine candidates according to dist
% and shrink list of candidates
%
% recursive algorithm: TAKE CARE many recursions needed

fprintf('r');
% end of recursion
if isempty(candidates),shrunkcandidates=[]; return; end
if size(candidates,2)==1 &sum(candidates==eps)==0,shrunkcandidates=[]; return; end

% recursive step
cand = candidates(:,1);
if feval(distfct, aicode', cand)   %zi = find(cand==eps & aicode~=eps);
  zi = find(cand==eps);
  if ~isempty(zi),
    ncandn = [cand(1:(zi-1)); -1; cand((zi+1):end)];
    ncandp = [cand(1:(zi-1)); 1; cand((zi+1):end)];
    candidates = [candidates(:,2:end) ncandp ncandn];
  else
    candidates = candidates(:,2:end);
  end
  shrunkcandidates = shrink(candidates,aicode,dist,distfct);
else
  shrunkcandidates = [cand shrink(candidates(:,2:end),aicode,dist,distfct)];
end
fprintf('o');

function shrunkcandidates = shrink(candidates, aicode, dist, distfct)
% refine candidates according to dist
% and shrink list of candidates
%
% iteration with dynamical list

%aicode
%candidates
i =1;
nb = size(candidates,2);
while i<=nb, 
  cand = candidates(:,i);
  if feval(distfct, aicode', cand)     zi = find(cand==eps);
    if ~isempty(zi),
      ncandn = [cand(1:(zi-1)); -1; cand((zi+1):end)];
      ncandp = [cand(1:(zi-1)); 1; cand((zi+1):end)];
      [candidates(:,[1:(i-1) (i+1):end]) ncandp ncandn];
      candidates = [candidates(:,[1:(i-1) (i+1):end]) ncandp ncandn];
    else
      candidates(:,[1:(i-1) (i+1):end]);
      candidates = candidates(:,[1:(i-1) (i+1):end]);
    end
  else
    i=i+1;
  end
  nb = size(candidates,2);
end
shrunkcandidates = candidates;

3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]Shaojiang Dong,Tianhong Luo,Bearing degradation process prediction based on the PCA and optimized LS-SVMmodel,Measurement,2013.06
 

4 Matlab代码实现