【Trajectory_planning】机械臂轨迹规划方法介绍

系列文章目录

提示：这里可以添加系列文章的所有文章的目录，目录需要自己手动添加
TODO:写完再整理

---

前言

认知有限，望大家多多包涵，有什么问题也希望能够与大家多交流，共同成长！

---

提示：以下是本篇文章正文内容

Trajectory_planning】机械臂轨迹规划
通常是说机械臂的路径规划

1、机器人带约束的轨迹规划理论

（1）机器人带约束的轨迹规划科普

复杂机器人系统（人形机器人、多足机器人和移动物体的机械臂等）【防盗标记–盒子君hzj】的运动规划轨迹和控制是富有挑战性的问题，机器人不仅需要时刻控制多个关节的自由度，还需要处理和环境物体之间的接触、摩擦以及碰撞，这些环境交互给机器人系统带来了非常复杂的运动约束。近年来基于优化的轨迹规划方法在很多机器人系统上得到了成功的应用

复杂的机器人系统通常是高自由度，欠驱动，非线性系统，【防盗标记–盒子君hzj】复杂的机器人系统会发生和环境的交互，特别是摩檫力和碰撞，轨迹规划和轨迹控制都必须通过记载计算机实时进行
.
.
.

（2）复杂机器人运动轨迹规划定义

（1）轨迹规划

【1】目的

根据动力学方程、机器人的约束和机器人生成起始点A终止点B，得到目标运动轨迹曲线【防盗标记–盒子君hzj】

【2】挑战

解决如何通过单个关节的运动实现机器人特定肢体的位移

【3】机器人约束类型

（1）机器人关节执行器的位置、速度、力矩约束
（2）机器人多个关节运动可能会被约束要耦合在一起
（3）一段时间内消耗的能量为定值

【4】轨迹规划的要求

（1）实时性：轨迹规划运行的求解速度必须达到20hz或者50hz，以便进行MPC或者满足控制的频率
（2）准确性：轨迹规划尽量精确的符合约束条件
（3）最好能解出轨迹规划的反馈控制器，反馈控制器能提高控制的稳定性【防盗标记–盒子君hzj】
.
.
.

（2）轨迹控制

【1】目的

根据目标运动轨迹曲线，得到机器人系统期望输入的控制量

【2】挑战

对每个关节进行独立的PID控制不一定能够实现整体的轨迹执行目标
.
.
.

（3）基础知识

（1）动力学方程

（1）机器人系统本质

用经典力学分析的质点系统

（2）动力学方程定义

（3）建立动力学方程例子

1）例子一：下落的球

2）例子二：倒立摆小车

3）多足机器人在复杂地形上的动力学模型【防盗标记–盒子君hzj】

.
.
.

（2）线性化

（1）目的

把复杂机器人的非线性系统进行线性化，【防盗标记–盒子君hzj】得到线性化的动力学方程（y=kx+b）表征原始的动力学方程，降低建模维度和计算量，提高实时性

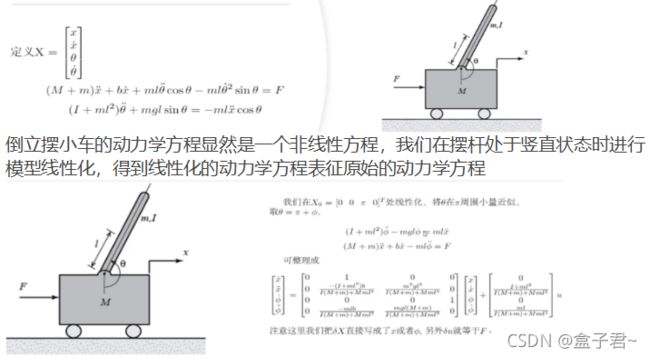
（2）使用泰勒公式展开的一阶泰勒公式进行线性化

（3）线性化的例子（倒立摆小车模型）

（4）线性化精度

非线性系统的线性化精度依赖于参考点的选取【防盗标记–盒子君hzj】，偏离参考点太远时，线性化方程会不准确
.
.
.

（3）线性二次型调节器（LQR）

（1）连续时间无穷时域的线性二次型调节器

【通过控制u0，使得O=f(x0,u0)的问题及求解】
【通常使用代价函数来描述】

.
.
.

（2）连续时间有穷时域的线性二次型调节器求解【现实情况】

.
.
.

（3）线性化和离散化的过程总结

.
.
.

（4）轨迹规划方法

（1）微分动态规划法（Differential Dynamic Programming)【非线性的线性化处理解决问题】

（1）数学原理

.
.

（2）原理的表述

.
.

（3）优点

（1）能获得最优的轨迹，也能活得最优的反馈控制器
（2）局部LQR问题的求解可以并行化计算，【防盗标记–盒子君hzj】能达到非常高的求解速度

（4）缺点

（1）需要较好的初始化轨迹
（2）比较难考虑额外的约束

.
.

（2）直接配点法（Direct Collocation）【直接对非线性化问题进行优化处理解决问题】

波士顿动力机器采用Direct Collocation作为机器人的云顶规划方法，在线生成轨迹和处理约束

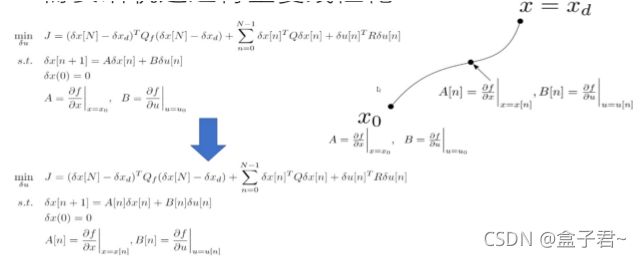
（1）直接配点法（Direct Collocation）原理

直接配点法（Direct Collocation）放弃获得反馈控制器，将轨迹上的每一时刻的状态和控制量看作一个非线性化优化问题的决策变量，通过成熟的非线性优化领域的技术来处理约束

.
.
.

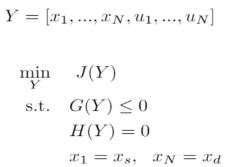
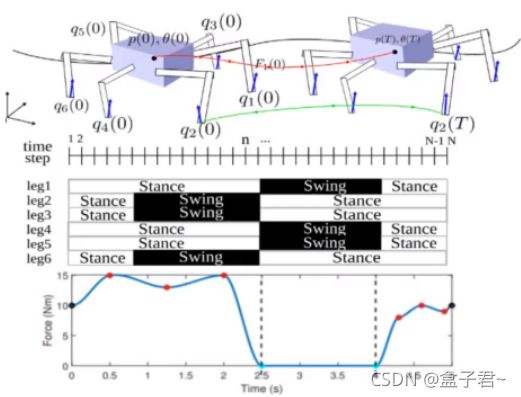
（2）直接配点法（Direct Collocation）例子(六足机器人)

（1）六足机器人的状态和控制量表述

（2）六足机器人构建非线性与优化问题构建
1）先把机器人在两点之间的运动轨迹全都看做决策变量
2）再构建非线性优化问题，【防盗标记–盒子君hzj】将运动的约束表示为优化问题的等式约束或者不等式约束
如下所示：

.
.
.

（3）六足机器人的约束介绍

1）机器人给定的起始位姿和终止位姿【这两个位姿可以通过机器人上电初始化得到】

2）足尖受到的地面作用力必须处在一个摩擦锥内，这样才能保证避免租佃打滑

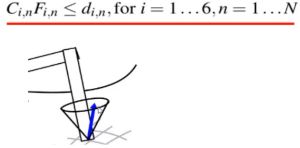
3）机器人在运动过程中，腿在swing和stance两个模式切换导致了腿在不同时刻会受到不同的约束，其中：
swing mode:腿在腾空状态，足端上的受力必须是

stance mode:腿在支撑状态，足端的运动速度必须是

4）直接配点法中最重要的约束：【防盗标记–盒子君hzj】对于运动轨迹上两个相邻的点，两个点之间的差必然等于动力学方程在两个时刻之间的积分量

.
.
.

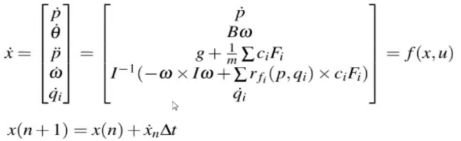
（4）六足机器人优化问题的求解

（1）问题引入
上面构建出来的优化问题仅仅适合用于公式表述，并不适合求解，因为假设多足机器人有200条腿（N=200），决策变量的维度是13200，维度太高，计算机时计算不出来的

（2）把轨迹表示成分段的多项式形式，决策变量
并不是轨迹上的点，而是多项式的系数

优点:
（1）大大减少了优化问题的维度
（2）自然地保证了运动的平滑性
（3）自然低加入约束条件
.
.

（3）直接配点法（Direct Collocation）优点
（1）可以处理任意高精度系统的动力学方程
（2）可以处理非常复杂的约束条件

*（4）直接配点法（Direct Collocation）缺点
（1）只能解出运动轨迹，不能获得反馈控制器
（2）非线性优化算法对于有些问题可能非常低效
.
.
.

（3）规划即推理法（planner As Inference）

这是是增强强化学习的基础，是近年来发展的新的轨迹规划方法
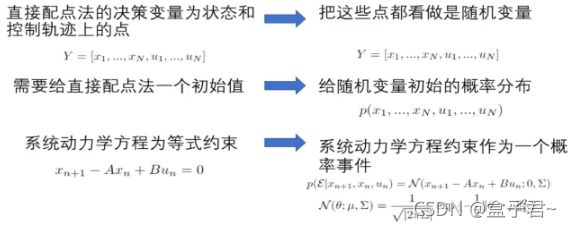
将轨迹规划看作最大后验概率估计问题，【防盗标记–盒子君hzj】建立最优控制和概率估计之间的联系

（1）将直接配点法的概念推广为条件概率分布

（2）轨迹规划作为最大后验概率估计

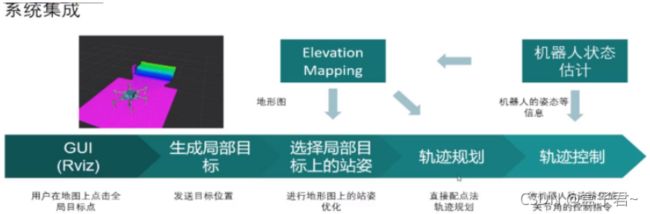
（5）机器人带约束的轨迹规划系统集成步骤

2、偏向于机械臂规划的应用库

（1）Open Motion Planning Library（OMPL）库

内置了RRT实现的各种算法（把算法打包成了库直接用就行）
官网链接：https://ompl.kavrakilab.org/

（2）机械臂控制moveit规划库

官网链接：https://moveit.ros.org/
https://industrial-training-master.readthedocs.io/en/melodic/_source/session4/Motion-Planning-CPP.html

3、熟悉机械臂/狗腿常见的轨迹规划算法

贝塞尔曲线\B样条、正弦余弦函数拟合、多项式函数拟合
.
.