最小生成树和最短路
这周是高产的一周,今天来讲讲图论:最小生成树和最短路:
******************这是一条分割线
最小生成树:一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。 最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。
效果:最小生成树能够保证整个拓扑图的所有路径之和最小,但不能保证任意两点之间是最短路径。
****************这是一条分割线
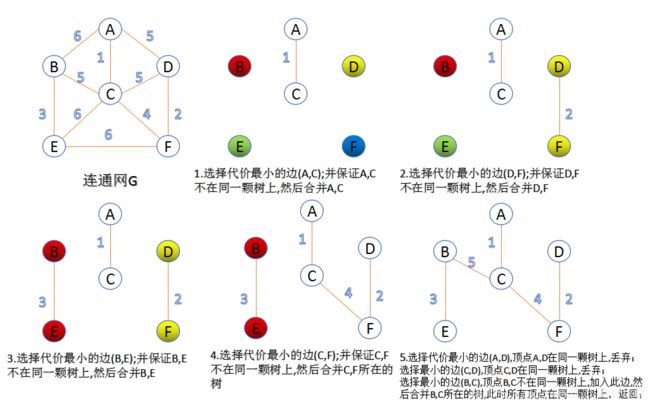
kruskal(克鲁斯卡尔)算法:
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。这是一个贪心的过程。
过程:
1.首先把所有的边权从小到大排序;
2. 把图中的n个顶点看成独立的n棵树组成的森林;
3. 选出权值最小两个点形成的边,u,v(u,v应属于不同的树),加入到生成树中;
4. 重复3的过程,直到所有点包括到生成树里或者生成树有n-1条边;
****************这是一条分割线
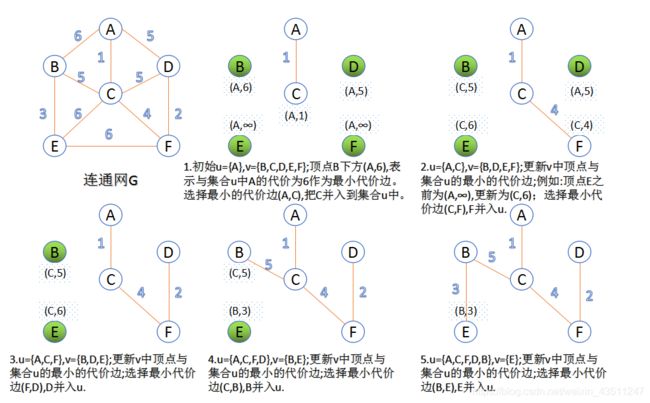
Prim算法:
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
过程:
1.令所有点的集合为V,任选一个点的的集合为U,未选到的点集合为V-U=VV;
2.在U和VV两个集合能组成的边中选一条权值最小的边加入到生成树中,并且更新集合;
3.重复2的过程,直到所有点包括到生成树里或者生成树有n-1条边;
****************这是一条分割线
prime算法时间复杂度o(n^2),适合稠密图,可以用二叉堆优化到0(m*log n),但是不如Kruskal算法简单。
#includeKruskal算法
时间复杂度O(m* log m)
#include*****************这是一条分割线
最短路
单源最短路径(single source shortest path ,SSPP问题),给定一张有向图G = (V,E),V是点集,E是边集,| V | = n ,| E | = m ,节点以[1,n]之间的连续整数编号,(x,y,z)表示一条从x出发,到达y,长度为z的有向边。设点1为起点,dist[i]表示从起点1到节点i的最短路径的长度。
Dijkstra算法:
过程:
1:初始化 dist[1]=0,其余节点的dist值为INF(无穷大);
2. 找出一个未被标记的,dist[x] 最小节点 x,然后标记节点x;
3. 扫描节点x的所有出边(x,y,z),若dist[x]+z < dist[y],则使用 dist[x]+z 更新dist[y];
4. 重复上述2-3的步骤,知道所有节点被标记;
*****************这是一条分割线
Dijkstra算法基于贪心思想,它只适用于所有边的长度都是非负数的图。当边长为非负数时,全局的最小值不可能再被其他的节点更新,故在第一步中选出的节点x必然满足:dist[x]已经是起点到x的最短路径。我们不断选择全局最小值进行标记和扩展,最终可得到起点1到每个节点的最短路径的长度。
*****************这是一条分割线
#include****************这是一条分割线
Bellman-Ford 和 SPFA 算法
****************这是一条分割线
给定一张有向图,若对图中的某一条(x,y,z),有dist[y]<=dist[x]+z成立,则该边慢走三角形不等式。若所有的边都满足三角形不等式,则dist数组就 是所求的最短路。
Bellman-Ford 算法过程:
1.扫描所有边(x,y,z),若dist[y] > dist[x]+z,则用 dist[x]+z更新dist[y]
2.重复上述步骤,知道没有更新操作发生。
Bellman-Ford 算法时间复杂度o(mn)
SPFA 算法就是“队列优化的 Bellman-Ford 算法”
过程
1.建立一个队列,最初队列中只含有起点1;
2.取出队列头部节点x,扫描它的所有出边(x,y,z),若dist[y] > dist[x]+z,则用 dist[x]+z更新dist[y].同时,若y不在队列中,则把y入队。
3.重复上述步骤,知道队列为空。
时间复杂度o(km),k为一个随机常数,但特殊构造的图上,很有可能退化成o(n*m)。
****************这是一条分割线
#include****************这是一条分割线
任意两点间的最短路:Floyd算法:dp大法好,
动态转移方程:d[k][i][j] = min(d[k-1][i][j],d[k-1][i][k]+d[k-1][k][j])
#include