CNN+LSTM+Attention实现时间序列预测
本文设计并实现的基于Attention机制的CNN-LSTM模型(以下简称为CLATT模型)一共分为五层,具体结构与原理如图所示。
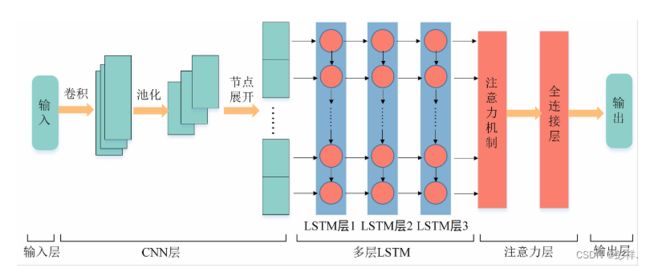
第一层是输入层。规定输入数据的格式(批大小,时间步数,特征维度),将批大小默认为1,时间
步数记为t,特征维度记为n,则一条样本可表示为一个实数序列矩阵Rt×n,记xi 为Rt×n 中第i个时间步数据的向量表示。
第二层是卷积神经网络层(CNN 层)。CNN 层可以提取数据中不同特征值之间的空间联系,进
而弥补 LSTM 无法捕获数据空间分量的缺点,同时它提取出的特征仍然具有时序性。样本数据进入CNN 层中会依次进行卷积、池化和节点展开(降维)操作。针对序列数据,本模型采取一维卷积,卷积核只按照单一的时域方向进行卷积。卷积核数目为r,尺寸设置为k,则xi:i+k-1为Rt×n中第i个时间步到第i+k-1个时间步的实数矩阵,滑动步长为1。权重矩阵 W1 是一个k×n 的实数矩阵。对每k 个时间步的序列向量进行一次特征提取,得到一个特征oi,计算公式如下:
oi =f(W1 ⊗xi:i+k-1 +b1)
f 是非线性的激活函数,b1 ∈R是一个偏置。当一个卷积核提取完一条样本的序列数据后,会得到一个(t-k+1)×1形状的特征图o ,计算公式如下:
o=[o1,o2,…,ot-k+1]T
CNN 共有r 个卷积核,因此最终会得到r 个特征图。卷积后再进行最大池化操作,池化尺寸为2,滑动步长为2,得到r 个[(t-k+1)/2]×1形状的特征图o ,计算公式如下:
o=max{oi,oi+1}(i=1,3,5,…,t-k)
这r 个特征图即为 CNN 层提取的特征,将其降维成一个长度为 r*(t-k+1)/2 的实数向量,该向量中保存了样本数据中不同特征值之间的空间联系,再输入LSTM 层中继续处理。
第三层是多层 LSTM。 LSTM具有记忆功能,可以提取建筑冷热负荷非线性数据的时序变化信
息。它引入了输入门、遗忘门、输出门,同时还添加了候选态、细胞态和隐状态。细胞态存储长期记
忆,可以缓解梯度消失,隐状态存储短期记忆。本模型采用了多层 LSTM,上一层 LSTM 的输出是下
一层的输入,一层一层往下传递,最后一层 LSTM 隐藏层的输出会进入注意力层进一步处理。
第四层是注意力层。注意力可以提高 LSTM中重要时间步的作用,从而进一步降低模型预测误
差。注意力本质上就是求最后一层 LSTM 输出向量的加权平均和。 LSTM 隐藏层输出向量作为注意力层的输入,通过一个全连接层进行训练,再对全连接层的输出使用 softmax 函数进行归一化,得出每一个隐藏层向量的分配权重,权重大小表示每个时间步的隐状态对于预测结果的重要程度。权重训练过程如下:
Si =tanh(WHi +bi)
αi =softmax(Si)
再利用训练出的权重对隐藏层输出向量求加权平均和,计算结果如下:
Ci = ∑ i = 0 k \sum_{i=0}^k ∑i=0kαiHi
其中 Hi 为最后一层LSTM 隐藏层的输出,Si 为每个隐藏层输出的得分,αi 为权重系数,Ci 为加权求和后的结果,softmax为激活函数。
第五层是输出层。该层规定了预测时间步ot,最终输出ot 步的预测结果。
def cnn_lstm_attention_model(n_input, n_out, n_features):
inputs = Input(shape=(n_input, n_features))
x = Conv1D(filters=64, kernel_size=1, activation='relu')(inputs) # , padding = 'same'
x = Dropout(0.3)(x)
lstm_out = Bidirectional(LSTM(128, return_sequences=True))(x)
lstm_out = Dropout(0.3)(lstm_out)
attention_mul = attention_block(lstm_out, n_input)
attention_mul = Flatten()(attention_mul)#扁平层,变为一维数据
output = Dense(n_out, activation='sigmoid')(attention_mul)
model = Model(inputs=[inputs], outputs=output)
model.summary()
model.compile(loss="mse", optimizer='adam')
return model
实验与分析
使用皮尔逊系数法进行相关性分析,选择相关系数绝对值大于等于5的特征作为实验数据的特征。
数据处理
首先,对缺失值和异常值进行处理,对缺失值采用前向填充法处理,对异常值采用标准差法进行
判断,再采用替换法进行处理。其次,将数据分别按照比例6∶2∶2划分成训练集、验证集和测试集。为防止测试集的信息泄露给模型,数据集的划分要放在归一化数据前。再次,为了加快模型训练速度,采用最大最小归一化方法处理数据集。最后,使用滑动窗口将时间序列数据转化为监督问题数据,滑动窗口大小为10,每次滑动1个时间步。
def series_to_supervised(data, n_in, n_out, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = list(), list()
# input sequence (t-n, ... t-1)
# 将3组输入数据依次向下移动3,2,1行,将数据加入cols列表(技巧:(n_in, 0, -1)中的-1指倒序循环,步长为1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# forecast sequence (t, t+1, ... t+n)
# 将一组输出数据加入cols列表(技巧:其中i=0)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# cols列表(list)中现在有四块经过下移后的数据(即:df(-3),df(-2),df(-1),df),将四块数据按列 并排合并
agg = concat(cols, axis=1)
# 给合并后的数据添加列名
agg.columns = names
print(agg)
# 删除NaN值列
if dropnan:
agg.dropna(inplace=True)
return agg
评估指标
本文选择平均绝对误差(MAE)和均方根误差(RMSE)以及R2作为误差评估指标,来定量地分析模型预测效果,公式如下:
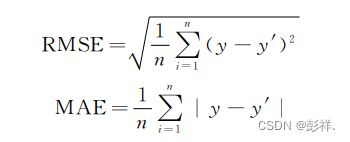
上述公式中,n 表示预测样本个数,y 表示真实值,y′表示预测值。
mean_absolute_error=mean_absolute_error(test_y[:, feature], predict_y[:, feature])
mean_squared_error=mean_squared_error(test_y[:, feature], predict_y[:, feature])
rmse=sqrt(mean_squared_error)#计算rmse
r2_score=r2_score(test_y[:, feature], predict_y[:, feature])#计算r平方
模型对比与分析
使用消融实验来进行模型对比
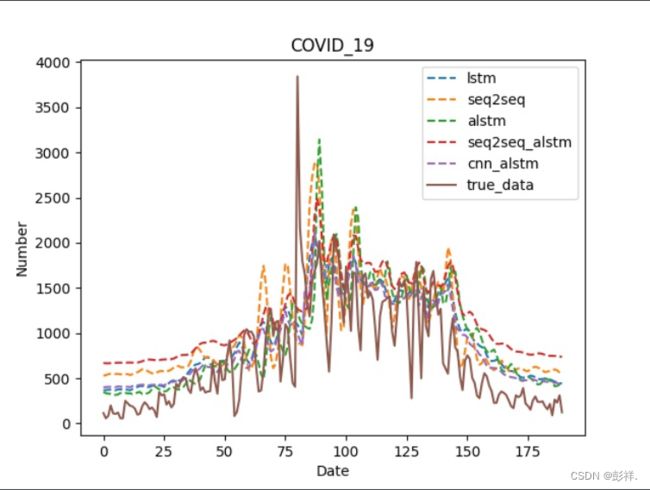
可以看到cnn_lstm_attention模型效果最好。
<function generate_lstm_model at 0x0000023BC73D9A60> rmse: 0.03718616235924552 r2: 0.4299815376427156
<function generate_seq2seq_model at 0x0000023BD9261598> rmse: 0.04570584783531429 r2: 0.13886797860359967
<function generate_attention_model at 0x0000023BD92651E0> rmse: 0.03876087350959183 r2: 0.3806825579394115
<function generate_seq2seq_attention_model at 0x0000023BDCEA1158> rmse: 0.04834780434038557 r2: 0.03643789488376792
<function cnn_lstm_attention_model at 0x0000023BDCF442F0> rmse: 0.03560436142032436 r2: 0.47744428499036307