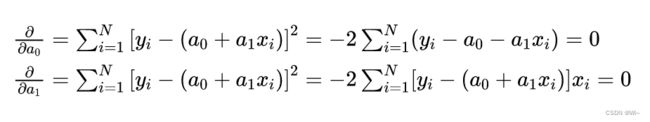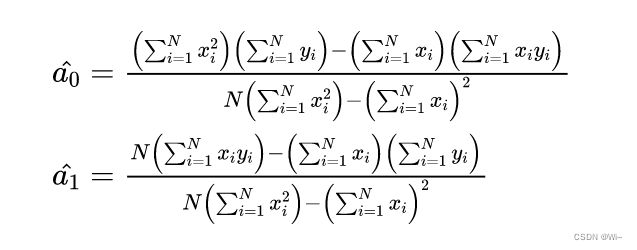最小二乘法，加权最小二乘法，迭代重加权最小二乘法
文章目录
-
- 一：最小二乘法（OLS）
-
- 1：概述
- 2：代数式
- 3：矩阵式（推荐）
-
- 3.1：实现代码
- 二：加权最小二乘法（WLS）
-
- 1：增加对角矩阵 W
-
- 1.1：实现代码
- 三：迭代重加权最小二乘法（IRLS）
- 四：应用
-
- 1:拟合圆
- 2: 曲线拟合
- 3：N点标定（包括9点标定）
- 五：总结
个人笔记：
最小二乘法，加权最小二乘法，迭代重加权最小二乘法。结合自己需要实现功能的目的，下面主要给出推导结果、代码实现和实际一些应用。推导过程最后会放一些个人参考的一些文章和资料。
一：最小二乘法（OLS）
1：概述
最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法是曲线拟合的常用方法，使用该方法对匹配函数的选取非常重要。。所谓匹配函数就是函数经过的路线在图中的点达到一个最佳匹配。不然就会出现过拟合和欠拟合的现象。
2：代数式
最小二乘法其思想主要是通过将理论值与预测值的距离的平方和达到最小。
举例：曲线拟合中最基本和最常用的是直线拟合。设x和y之间的函数关系为：一元一次函数（F(a0,a1)＝a0+a1x）y＝a0+a1x 代数推导：
分别对a0和a1求偏导
整理为方程组
然后化简得：
3：矩阵式（推荐）
举例：曲线拟合中最基本和最常用的是直线拟合。设x和y之间的函数关系为：一元一次函数（F(a0,a1)＝a0+a1x）y＝a0+a1x 使用矩阵表达：Ax = B
推导过程我会在最后放上链接。那么：
如果是一元多项式函数：
其中m代表多项式的阶数，离散点与该多项式的平方和 为F(a0,a1,…, am ) 。其中n代表采样点数：
一元多项式矩阵表达和一元一次项矩阵表达是一样的：Ax = B
3.1：实现代码
/* 普通最小二乘 Ax = B
* (A^T * A) * x = A^T * B
* x = (A^T * A)^-1 * A^T * B
*/
Array<double,Dynamic,1> GlobleFunction::leastSquares(Matrix<double,Dynamic,Dynamic> A, Matrix<double,Dynamic,1> B)
{
//获取矩阵的行数和列数
int rows = A.rows();
int col = A.cols();
//A的转置矩阵
Matrix<double,Dynamic,Dynamic> AT;
AT.resize(col,rows);
//x矩阵
Array<double,Dynamic,1> x;
x.resize(col,1);
//转置 AT
AT = A.transpose();
//x = (A^T * A)^-1 * A^T * B
x = ((AT * A).inverse()) * (AT * B);
return x;
}
Matrix是Eigen库中的一个矩阵类，这里引入Eigen库方便代数运算。
二：加权最小二乘法（WLS）
加权最小二乘法是对原模型进行加权，使之成为一个新的不存在异方差性的模型，然后采用普通最小二乘法估计其参数的一种数学优化技术。百度百科
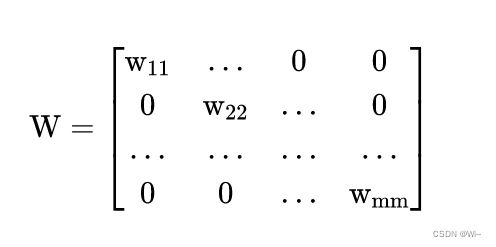
1：增加对角矩阵 W
在最小二乘法的基础上增加一个对角矩阵W，对每组数据赋予不同的权重。
W^T * W 对角矩阵每个数据的平方,消除负数。
1.1：实现代码
/* 加权最小二乘（WLS） W为对角线矩阵
* W²(Ax - B) = 0
* W²Ax = W²B
* (A^T * W^T * W * A) * x = A^T * W^T * W * B
* x = (A^T * W^T * W * A)^-1 * A^T * W^T * W * B
*/
Array<double,Dynamic,1> GlobleFunction::reweightedLeastSquares(Matrix<double,Dynamic,Dynamic> A, Matrix<double,Dynamic,1> B,Array<double,Dynamic,1> vectorW)
{
//获取矩阵的行数和列数
int rows = A.rows();
int col = A.cols();
//vectorW为空,默认构建对角线矩阵1
if(vectorW.isZero())
{
vectorW.resize(rows,1);
for(int i=0;i<rows;++i)
{
vectorW(i,0) = 1;
}
}
//A的转置矩阵
Matrix<double,Dynamic,Dynamic> AT;
AT.resize(col,rows);
//x矩阵
Array<double,Dynamic,1> x;
x.resize(col,1);
//W的转置矩阵
Matrix<double,Dynamic,Dynamic> WT,W;
W.resize(rows,rows);
WT.resize(rows,rows);
//生成对角线矩阵
W = vectorW.matrix().asDiagonal();
//转置
WT = W.transpose();
//转置 AT
AT = A.transpose();
// x = (A^T * W^T * W * A)^-1 * A^T * W^T * W * B
x = ((AT * WT * W * A).inverse()) * (AT * WT * W * B);
return x;
}
Matrix是Eigen库中的一个矩阵类，这里引入Eigen库方便代数运算。
三：迭代重加权最小二乘法（IRLS）
1：迭代重新加权最小二乘法( IRLS ) 的方法用于解决具有p 范数形式的目标函数的某些优化问题：维基百科
通过迭代方法，其中每一步都涉及解决以下形式的加权最小二乘问题：
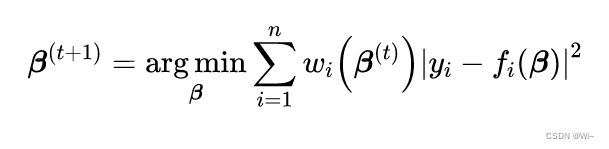
2：下面引入一片论文中的一段迭代方法求解 论文地址：Burrus, C.S. (2014). Iterative Reweighted Least Squares ∗.
MATLAB代码1：
% m-file IRLS0.m to find the optimal solution to Ax=b
% minimizing the L_p norm ||Ax-b||_p, using basic IRLS.
% csb 11/10/2012
function x = IRLS0(A,b,p,KK)
if nargin < 4, KK=10; end;
x = pinv(A)*b; % Initial L_2 solution
E = [];
for k = 1:KK % Iterate
e = A*x - b; % Error vector
w = abs(e).^((p-2)/2); % Error weights for IRLS
W = diag(w/sum(w)); % Normalize weight matrix
WA = W*A; % apply weights
x = (WA'*WA)\(WA'*W)*b; % weighted L_2 sol.
ee = norm(e,p); E = [E ee]; % Error at each iteration
end
plot(E)
MATLAB代码2：
% m-file IRLS1.m to find the optimal solution to Ax=b
% minimizing the L_p norm ||Ax-b||_p, using IRLS.
% Newton iterative update of solution, x, for M > N.
% For 2<p<infty, use homotopy parameter K = 1.01 to 2
% For 0<p<2, use K = approx 0.7 - 0.9
% csb 10/20/2012
function x = IRLS1(A,b,p,K,KK)
if nargin < 5, KK=10; end;
if nargin < 4, K = 1.5; end;
if nargin < 3, p = 10; end;
pk = 2; % Initial homotopy value
x = pinv(A)*b; % Initial L_2 solution
E = [];
for k = 1:KK % Iterate
if p >= 2, pk = min([p, K*pk]); % Homotopy change of p
else pk = max([p, K*pk]); end
e = A*x - b; % Error vector
w = abs(e).^((pk-2)/2); % Error weights for IRLS
W = diag(w/sum(w)); % Normalize weight matrix
WA = W*A; % apply weights
x1 = (WA'*WA)\(WA'*W)*b; % weighted L_2 sol.
q = 1/(pk-1); % Newton's parameter
if p > 2, x = q*x1 + (1-q)*x; nn=p; % partial update for p>2
else x = x1; nn=2; end % no partial update for p<2
ee = norm(e,nn); E = [E ee]; % Error at each iteration
end
plot(E)
C++代码：
/* 迭代重加权最小二乘（IRLS） W为权重,p为范数
* e = Ax - B
* W = e^(p−2)/2
* W²(Ax - B) = 0
* W²Ax = W²B
* (A^T * W^T * W * A) * x = A^T * W^T * W * B
* x = (A^T * W^T * W * A)^-1 * A^T * W^T * W * B
* 参考论文地址：https://www.semanticscholar.org/paper/Iterative-Reweighted-Least-Squares-%E2%88%97-Burrus/9b9218e7233f4d0b491e1582c893c9a099470a73
*/
Array<double,Dynamic,1> GlobleFunction::iterativeReweightedLeastSquares(Matrix<double,Dynamic,Dynamic> A, Matrix<double,Dynamic,1> B,double p,int kk)
{
/* x(k) = q x1(k) + (1-q)x(k-1)
* q = 1 / (p-1)
*/
//获取矩阵的行数和列数
int rows = A.rows();
int col = A.cols();
double pk = 2;//初始同伦值
double K = 1.5;
double epsilong = 10e-9; // ε
double delta = 10e-15; // δ
Array<double,Dynamic,1> x,_x,x1,e,w;
x.resize(col,1);
_x.resize(col,1);
x1.resize(col,1);
e.resize(rows,1);
w.resize(rows,1);
//初始x 对角矩阵w=1
x = reweightedLeastSquares(A,B);
//迭代 最大迭代次数kk
for(int i=0;i<kk;++i)
{
//保留前一个x值,用作最后比较确定收敛
_x = x;
if(p>=2)
{
pk = qMin(p,K*pk);
}
else
{
pk = qMax(p,K*pk);
}
//偏差
e = (A * x.matrix()) - B;
//偏差的绝对值// 求矩阵绝对值 ：e = e.cwiseAbs(); 或 e.array().abs().matrix()
e = e.abs();
//对每个偏差值小于delta,用delta赋值给它
for(int i=0;i<e.rows();++i)
{
e(i,0) = qMax(delta,e(i,0));
}
//对每个偏差值进行幂操作
w = e.pow(p/2.0-1);
w = w / w.sum();
x1 = reweightedLeastSquares(A,B,w);
double q = 1 / (pk-1);
if(p>2)
{
x = x1*q + x*(1-q);
}
else
{
x = x1;
}
//达到精度,结束
if((x-_x).abs().sum()<epsilong)
{
return x;
}
}
return x;
}
C++实现代码和MATLAB基本一样，不过有稍微改进，其中参考了维基百科和Burrus, C.S. (2014). Iterative Reweighted Least Squares ∗.
四：应用
以下针对超定方程组来求解的。数据个数大于未知数。
1:拟合圆
1：使用最小二乘效果，可以看出外部的噪点干扰还是比较大的。下面使用迭代重加权最小二乘算法优化。
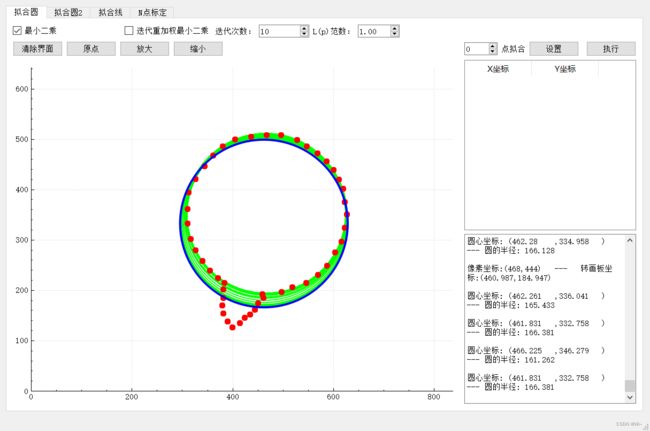2：迭代重加权最小二乘
第1次迭代
第2次迭代
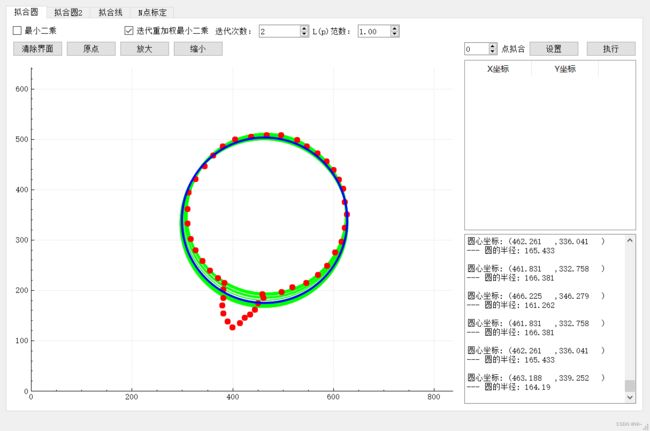第3次迭代
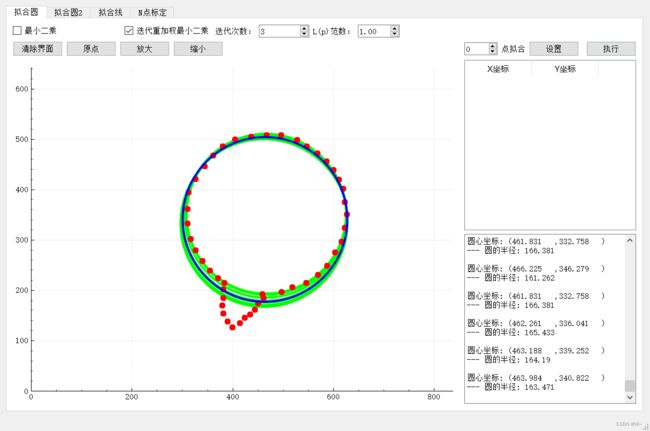第4次迭代
…
第20次迭代
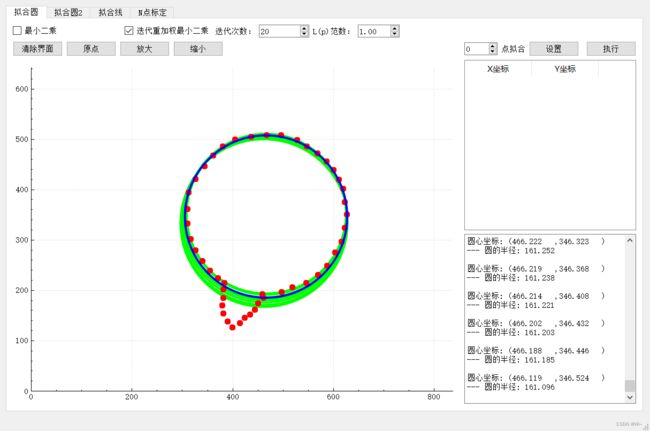
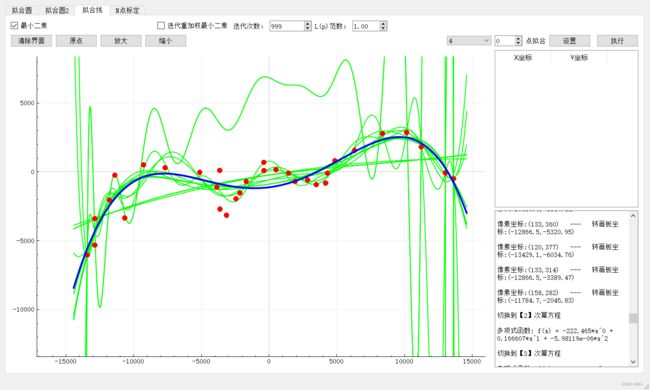
2: 曲线拟合
1：直线拟合 y = a0 + a1x
最小二乘：
1.2：迭代重加权最小二乘
第1次迭代
…
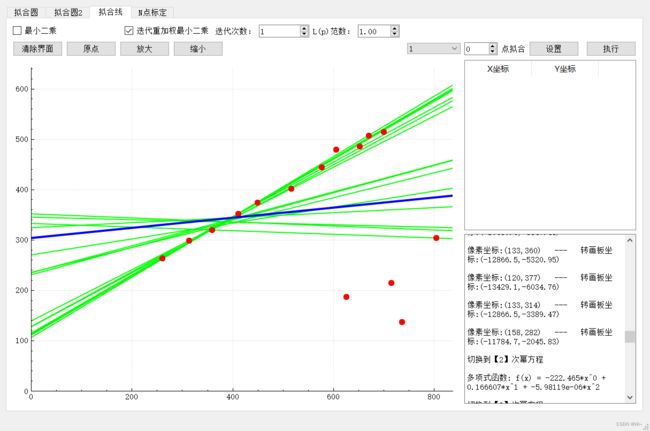第100次迭代
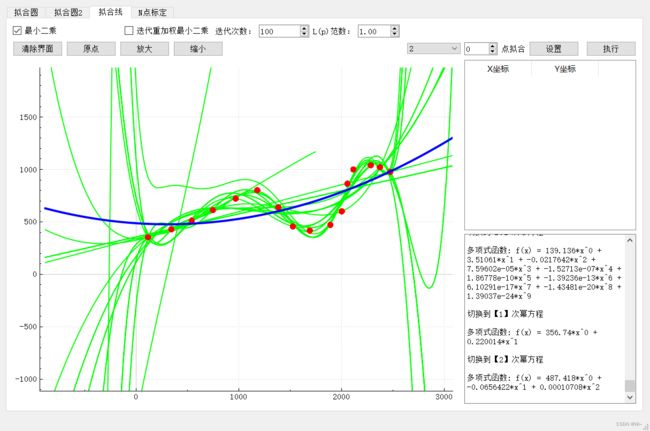
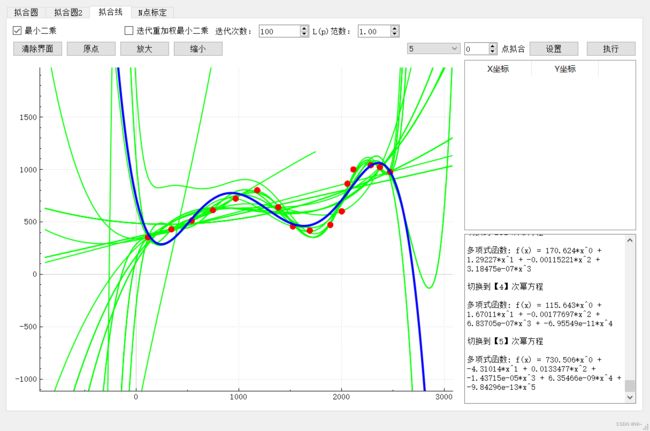
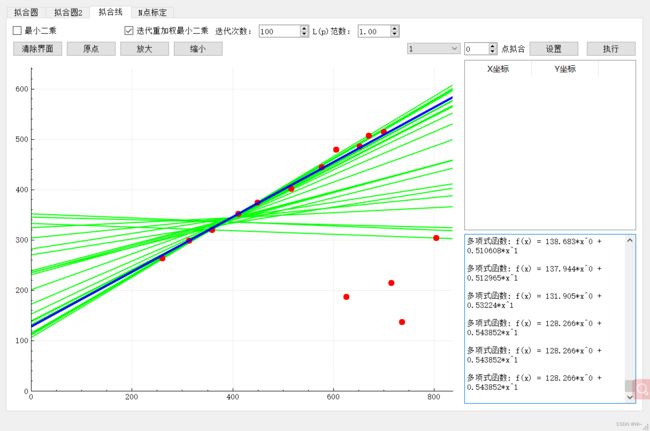2：最小二乘曲线拟合 ，寻找最佳次项函数
一次函数拟合：
二次函数拟合：
三次函数拟合：
四次函数拟合：
五次函数拟合：
六次函数拟合：
七次函数拟合：
八次函数拟合：
九次函数拟合：
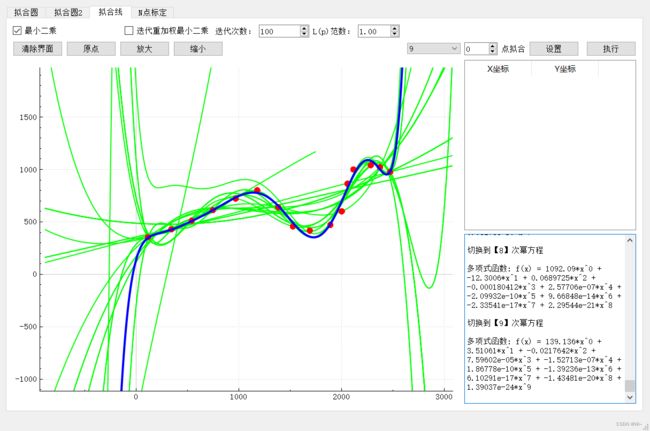
可以发现函数在第五次函数的时候拟合程度很好了，越往后越来过拟合了。
3：N点标定（包括9点标定）
9点标定是求视觉 中像素坐标和世界坐标建立的关系。
可以看到 halcon算子块 vector_to_hom_mat2d 就是用最小二乘法来计算矩阵的。图中外部算法【2】其实是本文章中的最小二乘算法实现的。内部算法【1】实现是用求偏导计算的，在这篇文章有实现N点标定
五：总结
1：工具：主要Qt + Eigen库 + QCustomPlot类
Eigen库是一个用于矩阵计算，代数计算库
QCustomPlot类是一个用于绘图和数据可视化
2：上面完整代码已上传GitHub
3：其他链接
最小二乘代数推导
最小二乘矩阵推导
最小二乘法？为神马不是差的绝对值
正则化
鲁棒学习算法
最小二乘法的原理理解
