N点标定-坐标系变换
文章目录
-
- 1：标定算法
- 2：外部链接
1：标定算法
vector_to_hom_mat2d(Px, Py, Qx, Qy, HomMat2D)
这里参考了halcon算子块的官方文档，使用的是最小二乘法，求HomMat2D矩阵。 -常用九点标定，求两个坐标系的坐标转换。。
下面个人实现原理，结果和上面算子算出来的结果一致，知识有限，仅供学习交流。
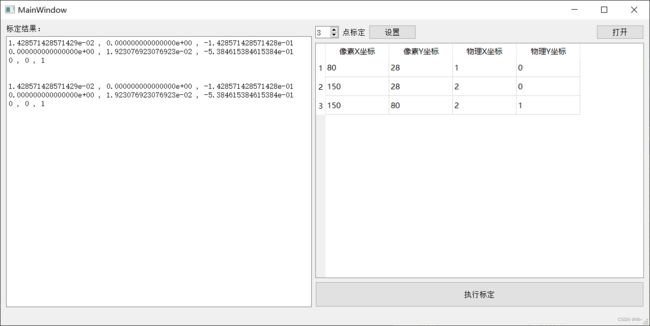
1：先来看一张图，图中矩阵为2行3列，最后一列为0,0,1；因为用到是齐次矩阵，所以展开就省略了。具体为什么是这样的矩阵形式，其实是一系列的变换，也就是平面二维仿射变换。
2：然后使用最小二乘法列出项（最小平方法）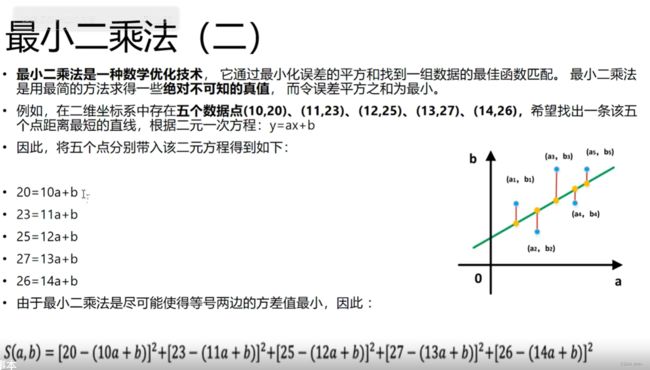
其次在对每个未知量进行求偏导，图中是两个未知量，就是列出两个方程组，如果是三个未知量，那就是三个方程组
三个未知量进行求导，得出来的结果就是对应矩阵里的未知量。。
3：上面方法都是笔记上演示，如果放在程序里怎么做呢？用上面这种怎么求未知量呢？下面会有个人实现的源代码，这里求方程组使用克拉默法则，列出行列式进行求解，放在代码里，方便求解。
正确的做法就是求各个未知量的系数，比如：
4：核心代码演示
//保存从界面获取的坐标数据
struct _coordList{
QList<QPair<double,double>> pixPoines;//保存像素坐标
QList<QPair<double,double>> physicsPoines;//保存物理坐标
};
//保存最小二乘法三个未知量(a,b,c)的结果
struct _squareLaw{
double aa=0;
double bb=0;
double cc=0;
double ab=0;
double ac=0;
double bc=0;
double _a=0;
double _b=0;
double _c=0;
};
//导数3x4
struct _differentialCoefficient{
QList<double> diff_a;
QList<double> diff_b;
QList<double> diff_c;
};
//矩阵3X3
struct _mat{
double a=0;
double b=0;
double c=0;
double d=0;
double e=0;
double f=0;
double g=0;
double h=0;
double i=0;
};
//标定
_mat MainWindow::calibration(_coordList coordL)
{
//保存未知量（a,b,c）的系数
_squareLaw squareLaw_x;
_squareLaw squareLaw_y;
for(int i=0;i<coordL.pixPoines.count();i++) {
squareLaw_x.aa += pow(coordL.pixPoines.at(i).first,2)*2;
squareLaw_x.bb += pow(coordL.pixPoines.at(i).second,2)*2;
squareLaw_x.cc += 1*2;
squareLaw_x.ab += coordL.pixPoines.at(i).first*coordL.pixPoines.at(i).second*2;
squareLaw_x.ac += coordL.pixPoines.at(i).first*2;
squareLaw_x.bc += coordL.pixPoines.at(i).second*2;
squareLaw_x._a += coordL.pixPoines.at(i).first*coordL.physicsPoines.at(i).first*2;
squareLaw_x._b += coordL.pixPoines.at(i).second*coordL.physicsPoines.at(i).first*2;
squareLaw_x._c += coordL.physicsPoines.at(i).first*2;
}
for(int i=0;i<coordL.pixPoines.count();i++) {
squareLaw_y.aa += pow(coordL.pixPoines.at(i).first,2)*2;
squareLaw_y.bb += pow(coordL.pixPoines.at(i).second,2)*2;
squareLaw_y.cc += 1*2;
squareLaw_y.ab += coordL.pixPoines.at(i).first*coordL.pixPoines.at(i).second*2;
squareLaw_y.ac += coordL.pixPoines.at(i).first*2;
squareLaw_y.bc += coordL.pixPoines.at(i).second*2;
squareLaw_y._a += coordL.pixPoines.at(i).first*coordL.physicsPoines.at(i).second*2;
squareLaw_y._b += coordL.pixPoines.at(i).second*coordL.physicsPoines.at(i).second*2;
squareLaw_y._c += coordL.physicsPoines.at(i).second*2;
}
//求导数 3元方程组系数
_differentialCoefficient diff_x;
_differentialCoefficient diff_y;
diff_x.diff_a.append(squareLaw_x.aa);
diff_x.diff_a.append(squareLaw_x.ab);
diff_x.diff_a.append(squareLaw_x.ac);
diff_x.diff_a.append(squareLaw_x._a);
diff_x.diff_b.append(squareLaw_x.ab);
diff_x.diff_b.append(squareLaw_x.bb);
diff_x.diff_b.append(squareLaw_x.bc);
diff_x.diff_b.append(squareLaw_x._b);
diff_x.diff_c.append(squareLaw_x.ac);
diff_x.diff_c.append(squareLaw_x.bc);
diff_x.diff_c.append(squareLaw_x.cc);
diff_x.diff_c.append(squareLaw_x._c);
diff_y.diff_a.append(squareLaw_y.aa);
diff_y.diff_a.append(squareLaw_y.ab);
diff_y.diff_a.append(squareLaw_y.ac);
diff_y.diff_a.append(squareLaw_y._a);
diff_y.diff_b.append(squareLaw_y.ab);
diff_y.diff_b.append(squareLaw_y.bb);
diff_y.diff_b.append(squareLaw_y.bc);
diff_y.diff_b.append(squareLaw_y._b);
diff_y.diff_c.append(squareLaw_y.ac);
diff_y.diff_c.append(squareLaw_y.bc);
diff_y.diff_c.append(squareLaw_y.cc);
diff_y.diff_c.append(squareLaw_y._c);
//解方程 使用克莱默法则解方程
//a11a22a33+a12a23a31+a13a21a32 −a13a22a31−a11a23a32−a12a21a33
double D_x,Da,Db,Dc, D_y,Dd,De,Df;
D_x = diff_x.diff_a.at(0)*diff_x.diff_b.at(1)*diff_x.diff_c.at(2) + diff_x.diff_a.at(1)*diff_x.diff_b.at(2)*diff_x.diff_c.at(0) +diff_x.diff_a.at(2)*diff_x.diff_b.at(0)*diff_x.diff_c.at(1)
-diff_x.diff_a.at(2)*diff_x.diff_b.at(1)*diff_x.diff_c.at(0) - diff_x.diff_a.at(0)*diff_x.diff_b.at(2)*diff_x.diff_c.at(1) -diff_x.diff_a.at(1)*diff_x.diff_b.at(0)*diff_x.diff_c.at(2);
Da = diff_x.diff_a.at(3)*diff_x.diff_b.at(1)*diff_x.diff_c.at(2) + diff_x.diff_a.at(1)*diff_x.diff_b.at(2)*diff_x.diff_c.at(3) +diff_x.diff_a.at(2)*diff_x.diff_b.at(3)*diff_x.diff_c.at(1)
-diff_x.diff_a.at(2)*diff_x.diff_b.at(1)*diff_x.diff_c.at(3) - diff_x.diff_a.at(3)*diff_x.diff_b.at(2)*diff_x.diff_c.at(1) -diff_x.diff_a.at(1)*diff_x.diff_b.at(3)*diff_x.diff_c.at(2);
Db = diff_x.diff_a.at(0)*diff_x.diff_b.at(3)*diff_x.diff_c.at(2) + diff_x.diff_a.at(3)*diff_x.diff_b.at(2)*diff_x.diff_c.at(0) +diff_x.diff_a.at(2)*diff_x.diff_b.at(0)*diff_x.diff_c.at(3)
-diff_x.diff_a.at(2)*diff_x.diff_b.at(3)*diff_x.diff_c.at(0) - diff_x.diff_a.at(0)*diff_x.diff_b.at(2)*diff_x.diff_c.at(3) -diff_x.diff_a.at(3)*diff_x.diff_b.at(0)*diff_x.diff_c.at(2);
Dc = diff_x.diff_a.at(0)*diff_x.diff_b.at(1)*diff_x.diff_c.at(3) + diff_x.diff_a.at(1)*diff_x.diff_b.at(3)*diff_x.diff_c.at(0) +diff_x.diff_a.at(3)*diff_x.diff_b.at(0)*diff_x.diff_c.at(1)
-diff_x.diff_a.at(3)*diff_x.diff_b.at(1)*diff_x.diff_c.at(0) - diff_x.diff_a.at(0)*diff_x.diff_b.at(3)*diff_x.diff_c.at(1) -diff_x.diff_a.at(1)*diff_x.diff_b.at(0)*diff_x.diff_c.at(3);
D_y = diff_y.diff_a.at(0)*diff_y.diff_b.at(1)*diff_y.diff_c.at(2) + diff_y.diff_a.at(1)*diff_y.diff_b.at(2)*diff_y.diff_c.at(0) +diff_y.diff_a.at(2)*diff_y.diff_b.at(0)*diff_y.diff_c.at(1)
-diff_y.diff_a.at(2)*diff_y.diff_b.at(1)*diff_y.diff_c.at(0) - diff_y.diff_a.at(0)*diff_y.diff_b.at(2)*diff_y.diff_c.at(1) -diff_y.diff_a.at(1)*diff_y.diff_b.at(0)*diff_y.diff_c.at(2);
Dd = diff_y.diff_a.at(3)*diff_y.diff_b.at(1)*diff_y.diff_c.at(2) + diff_y.diff_a.at(1)*diff_y.diff_b.at(2)*diff_y.diff_c.at(3) +diff_y.diff_a.at(2)*diff_y.diff_b.at(3)*diff_y.diff_c.at(1)
-diff_y.diff_a.at(2)*diff_y.diff_b.at(1)*diff_y.diff_c.at(3) - diff_y.diff_a.at(3)*diff_y.diff_b.at(2)*diff_y.diff_c.at(1) -diff_y.diff_a.at(1)*diff_y.diff_b.at(3)*diff_y.diff_c.at(2);
De = diff_y.diff_a.at(0)*diff_y.diff_b.at(3)*diff_y.diff_c.at(2) + diff_y.diff_a.at(3)*diff_y.diff_b.at(2)*diff_y.diff_c.at(0) +diff_y.diff_a.at(2)*diff_y.diff_b.at(0)*diff_y.diff_c.at(3)
-diff_y.diff_a.at(2)*diff_y.diff_b.at(3)*diff_y.diff_c.at(0) - diff_y.diff_a.at(0)*diff_y.diff_b.at(2)*diff_y.diff_c.at(3) -diff_y.diff_a.at(3)*diff_y.diff_b.at(0)*diff_y.diff_c.at(2);
Df = diff_y.diff_a.at(0)*diff_y.diff_b.at(1)*diff_y.diff_c.at(3) + diff_y.diff_a.at(1)*diff_y.diff_b.at(3)*diff_y.diff_c.at(0) +diff_y.diff_a.at(3)*diff_y.diff_b.at(0)*diff_y.diff_c.at(1)
-diff_y.diff_a.at(3)*diff_y.diff_b.at(1)*diff_y.diff_c.at(0) - diff_y.diff_a.at(0)*diff_y.diff_b.at(3)*diff_y.diff_c.at(1) -diff_y.diff_a.at(1)*diff_y.diff_b.at(0)*diff_y.diff_c.at(3);
_mat mat;
mat.a = Da/D_x;
mat.b = Db/D_x;
mat.c = Dc/D_x;
mat.d = Dd/D_y;
mat.e = De/D_y;
mat.f = Df/D_y;
mat.g = 0;
mat.h = 0;
mat.i = 1;
return mat;
}
完整代码实现xxx.h
#ifndef MAINWINDOW_H
#define MAINWINDOW_H
#include xxx.cpp
#include "mainwindow.h"
#include "ui_mainwindow.h"
#include 
2：外部链接
最小二乘法
仿射变换
克拉默法则
行列式计算方法
2D坐标系下的点的转换矩阵