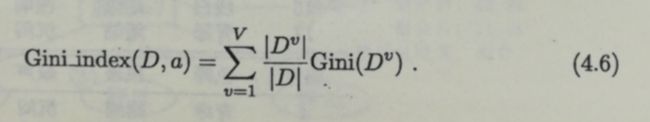决策树算法分析

本文是根据西瓜书对决策树进行分析的。

决策树的递归流程：

函数：TreeGenerate(D,A):

初始传入参数训练集为D（比如n个西瓜），传入参数属性为A（比如色泽、根蒂、纹理、触感。。。）

①拿过来一个新生成的结点（第一次走这个过程的话就是根节点）

②如果到达这个结点的训练集D中的样本全部属于某个类别标签C，那么就不用再分了，直接把这个结点设置为叶子结点，其类别标签为C，结束返回。

③否则，如果已经没有属性可以划分了（即A为空，因为每根据信息熵生成一个父节点就意味着已经用过一个属性， 可选的属性就少了一个）或者D中的样本在这个结点的众多属性A中的取值唯一，则标记这个结点为叶子结点，同时设置其类别标签为D中样本数最多的类别，结束返回。

④否则，根据信息熵或者巴拉巴拉找到A中的最优划分属性a,Da为到达a结点的样本集，然后对每一个属性a做下面的事情。

⑤如果Da为空（即训练集中没有数据能到达这个结点），则把这个属性结点a定义为叶子结点，类别标签为D中样本最多的类。

⑥否则（经过了这么多层筛选，这个基点终于可以作为父节点进行划分了），以a为分支节点重走上面的流程，返回TreeGenerate（Da,A-a）A-a的意思是去除属性a

划分属性的依据（特征选择）：

1.信息增益（ID3决策树学习算法就是按照信息增益进行划分的）

先来看一看什么是信息熵：

信息熵是度量样本集合纯度最常用的一种指标。

假定当前样本集合D中第K类样本所占比例为pk，则D的信息熵定义为

很明显，熵嘛，是混乱程度的意思，信息熵越小，则D的纯度越高。

信息增益就是用信息熵来表示使用某个属性对于“纯度的提升”最大。

一般而言，信息增益越大意味着使用属性a来进行划分所获得的“纯度提升”越大。

这样我们就知道划分选择的过程了。

对于样本D，有属性集A(a1,a2,a3,...)，对A中每一个属性ai（比如色泽？），它可能有v个取值（比如圆润？），每个取值都对应一堆符合的样本Dv，那么我们首先根据上面式子4.2计算出ai的信息增益，然后计算其他的属性ai的信息增益，选出信息增益最大的那个属性，他就是接下来我们要进行划分的父节点。

2.增益率（C4.5决策树学习算法就是按照信息增益进行划分的）

上面用信息增益来划分有个缺点，就是对于可取值数目较多的属性有所偏好，为了减少这种偏好可能带来的不利影响，著名的C4.5决策树算法不直接用信息增益，而是使用增益率来选择最优的划分属性。

增益率：

其中

上式称为属性a的固有值，属性a可能的取值数目越多（即V越大），则IV(a)的值通常会越大。这样就会削弱可取值多对某些属性的信息增益的提高。

需要注意的是，这样的话，C4.5算法取的就不是信息增益最大的属性，而是削弱后的信息增益最大的属性，这是一个启发式。

3.基尼指数（CART决策树使用基尼指数）

CART是Classification and Regression Tree的简称，这是一种著名的决策树学习算法，分类和回归任务都可以使用。

数据集D的纯度可以用基尼值来度量：

直观的说，他反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此，越小则纯度越高。

属性a的基尼指数：

选择使得划分后基尼指数最小的属性作为最优划分属性。

剪枝

何为剪枝？其实就是判断这个属性要不要根据属性值的不同进行展开，就是决定一个节点是叶子结点还是父节点。

剪枝分为两种，一种是预剪枝，另一种是后剪枝，我们挨个来分析

原决策树：

预剪枝

预剪枝就是在生成决策树的过程中进行剪枝，用这么几句话可以大体概括：

我假设将节点a划分为叶子结点，那么此时节点a的类别即为它的父节点包含的所有样本中类别最多的那个类别，计算划分正确的概率p1。然后我们假设这个节点a为父节点（根据信息增益或者增益率或者基尼指数决定这个a节点是哪个属性），根据其属性取值不同，比如假如a是光泽属性，分为暗淡、明亮两个取值，根据这个取值不同划分样本，得到两个叶子结点，对每个叶子节点而言，叶子节点中哪一个类别的样本的数量多这个叶子结点的类别标签就是哪个，然后我们对样本进行划分了，再计算一次正确率p2。如果p2>p1则这个节点可以划分a属性，否则，不能继续划分，就单单作为一个叶子结点，也就是进行了剪枝。

另一种规范的表述：

决策树常用的剪枝常用的简直方法有两种：预剪枝(Pre-Pruning)和后剪枝(Post-Pruning)。预剪枝是根据一些原则及早的停止树增长，如树的深度达到用户所要的深度、节点中样本个数少于用户指定个数、不纯度指标下降的最大幅度小于用户指定的幅度等。预剪枝的核心问题是如何事先指定树的最大深度，如果设置的最大深度不恰当，那么将会导致过于限制树的生长，使决策树的表达式规则趋于一般，不能更好地对新数据集进行分类和预测。除了事先限定决策树的最大深度之外，还有另外一个方法来实现预剪枝操作，那就是采用检验技术对当前结点对应的样本集合进行检验，如果该样本集合的样本数量已小于事先指定的最小允许值，那么停止该结点的继续生长，并将该结点变为叶子结点，否则可以继续扩展该结点。

西瓜书80,81页有具体实例，不举例了。

总结：可以看出预剪枝使得很多属性都没有展开，降低了过拟合的风险，还显著减少了训练时间开销和测试时间开销。but，你想啊，你禁止了一个分支的展开，只是说明这个分支展开降低了泛化性能，但是有没有可能这个分支展开之后再展开反而会提高泛化性能呢？有可能。所以预剪枝还是有缺点的，他使得欠拟合的风险提高。

预剪枝后：

后剪枝

后剪枝就是在生成决策树之后再进行剪枝，用下面这么几句话进行概括：

其实就是先生成决策树，然后倒过来从最底层的父节点开始，判断删除它并且变成叶子结点之后，划分的正确率是否高于当前不删除，划分的正确率。明白了预剪枝之后后剪枝就很容易明白了，西瓜书上也有具体例子，这里不用讲大家应该也可以明白了。

另一种规范的表述：

后剪枝则是通过在完全生长的树上剪去分枝实现的，通过删除节点的分支来剪去树节点，可以使用的后剪枝方法有多种，比如：代价复杂性剪枝、最小误差剪枝、悲观误差剪枝等等。后剪枝操作是一个边修剪边检验的过程，一般规则标准是：在决策树的不断剪枝操作过程中，将原样本集合或新数据集合作为测试数据，检验决策树对测试数据的预测精度，并计算出相应的错误率，如果剪掉某个子树后的决策树对测试数据的预测精度或其他测度不降低，那么剪掉该子树。

总结：后剪枝比预剪枝保留了一些分支，（因为它相比预剪枝避免了一个情况，那就是避免了禁止一个分支展开会直接抹杀这个分支展开后再展开对于正确率反而增加的情况），所以欠拟合风险变小，泛化性能往往优于预剪枝。但是后剪枝是在已经生成完全决策树之后进行的，并且要自上而下对于所有父节点进行考察，训练时间开销远远大于不进行剪枝操作的决策树和预剪枝决策树。

后剪枝后：

决策树特点：

优点：

计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。
准确性高: 挖掘出来的分类规则准确性高, 便于理解, 决策树可以清晰的显示哪些字段比较重要, 即可以生成可以理解的规则。
可以处理连续和离散字段
不需要任何领域知识和参数假设
适合高维数据
缺点：
对于各类别样本数量不一致的数据, 信息增益偏向于那些更多数值的特征
容易过拟合
忽略属性之间的相关性

适用数据类型：数值型和标称型