Saisimonzs

机器学习算法系列（五）- Lasso回归算法（Lasso Regression Algorithm）

阅读本文需要的背景知识点：线性回归算法、一丢丢编程知识

最近笔者做了一个基于人工智能实现音乐转谱和人声分离功能的在线应用——反谱（Serocs），感兴趣的读者欢迎试用与分享，感谢您的支持！serocs.cn

一、引言

上一节我们学习了解决多重共线性的一种方法是对代价函数正则化，其中一种正则化的算法叫岭回归算法（Ridge Regression Algorithm）。下面我们来学习另一种正则化的算法 - Lasso回归算法¹（Lasso Regression Algorithm），LASSO的完整名称叫最小绝对值收敛和选择算子算法（least absolute shrinkage and selection operator）。

二、模型介绍

先来回顾一下岭回归的代价函数，在原来标准线性回归代价函数上加上了一个带惩罚系数 λ 的 w 向量的 L2-范数的平方：
$\operatorname{Cost}(w) = \sum_{i = 1}^N \left( y_i - w^Tx_i \right)^2 + \lambda\|w\|_{2}^{2}$

Lasso回归算法也同岭回归一样加上了正则项，只是改成加上了一个带惩罚系数 λ 的 w 向量的 L1-范数作为惩罚项（L1-范数的含义为向量 w 每个元素绝对值的和），所以这种正则化方式也被称为L1正则化。
$\operatorname{Cost}(w) = \sum_{i = 1}^N \left( y_i - w^Tx_i \right)^2 + \lambda\|w\|_1$

同样是求使得代价函数最小时 w 的大小：
$\underset{w}{\operatorname{argmin}}\left(\sum_{i = 1}^N \left( y_i - w^Tx_i \right)^2 + \lambda\|w\|_1\right)$

由于加入的是向量的 L1-范数，其中存在绝对值，导致其代价函数不是处处可导的，所以就没办法通过直接求导的方式来直接得到 w 的解析解。下面介绍两种求解权重系数 w 的方法：坐标下降法²（coordinate descent）、最小角回归法³（Least Angle Regression，LARS）

三、算法步骤

坐标下降法：
坐标下降法的核心与它的名称一样，就是沿着某一个坐标轴方向，通过一次一次的迭代更新权重系数的值，来渐渐逼近最优解。

具体步骤：
（1）初始化权重系数 w，例如初始化为零向量。
（2）遍历所有权重系数，依次将其中一个权重系数当作变量，其他权重系数固定为上一次计算的结果当作常量，求出当前条件下只有一个权重系数变量的情况下的最优解。
在第 k 次迭代时，更新权重系数的方法如下：
$\begin{matrix} w_m^k 表示第k次迭代，第m个权重系数 \\ w_1^k = \underset{w_1}{\operatorname{argmin}} \left( \operatorname{Cost}(w_1, w_2^{k-1}, \dots, w_{m-1}^{k-1}, w_m^{k-1}) \right) \\ w_2^k = \underset{w_2}{\operatorname{argmin}} \left( \operatorname{Cost}(w_1^{k}, w_2, \dots, w_{m-1}^{k-1}, w_m^{k-1}) \right) \\ \vdots \\ w_m^k = \underset{w_m}{\operatorname{argmin}} \left( \operatorname{Cost}(w_1^{k}, w_2^{k}, \dots, w_{m-1}^{k}, w_m) \right) \\ \end{matrix}$

（3）步骤（2）为一次完整迭代，当所有权重系数的变化不大或者到达最大迭代次数时，结束迭代。

By Nicoguaro - Own work

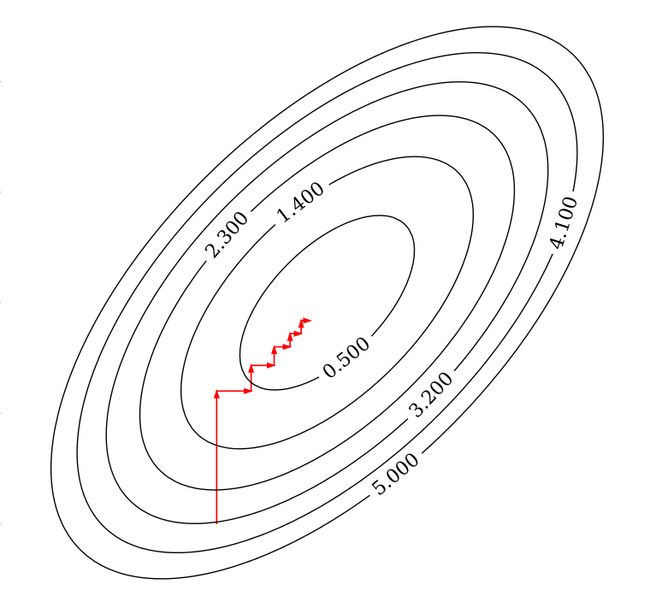
如上图所示，每次迭代固定其他的权重系数，只朝着其中一个坐标轴的方向更新，最后到达最优解。

最小角回归法：
最小角回归法是一种特征选择的方法，计算出每个特征的相关性，通过数学公式逐渐计算出最优解。

具体步骤：
（1）初始化权重系数 w，例如初始化为零向量。
（2）初始化残差向量 residual 为目标标签向量 $y - Xw$ ，由于此时 w 为零向量，所以残差向量等于目标标签向量 y
（3）选择一个与残差向量相关性最大的特征向量 $x_i$ ，沿着特征向量 $x_i$ 的方向找到一组权重系数 w，出现另一个与残差向量相关性最大的特征向量 $x_j$ 使得新的残差向量 residual 与这两个特征向量的相关性相等（即残差向量等于这两个特征向量的角平分向量上），重新计算残差向量。
（4）重复步骤（3），继续找到一组权重系数 w，使得第三个与残差向量相关性最大的特征向量 $x_k$ 使得新的残差向量 residual 与这三个特征向量的相关性相等（即残差向量等于这三个特征向量的等角向量上），以此类推。
（5）当残差向量 residual 足够小或者所有特征向量都已被选择，结束迭代。

Least Angle Regression - Figure 2

上图演示了只有两个特征向量时的情况，初始残差向量为 $y_2$ ，其中 $x_1$ 向量与残差向量的相关性最大（向量夹角最小），找到一个 $θ_{11}$ 使得新的残差向量 $y_2 - x_1 * θ_{11}$ 是 $x_1$ 和 $x_2$ 的角平分线（图中为 $u_2$ ），此时 $w_1 = θ_{11}$ , $w_2 = 0$ 。最后找到一组 $θ_{21}$ ， $θ_{22}$ 使得新的残差向量 $y_2 - x_1 * θ_{11} - (x_1 * θ_{21} + x_2 * θ_{22})$ 尽可能小，此时 $w_1 = θ_{11} + θ_{21}$ ， $w_2 = θ_{22}$ 。所有特征向量都已被选择，所以结束迭代。

坐标下降法相对最小角回归法相对好理解一些，每次只需要关心一个权重系数即可。最小角回归法则是通过一些巧妙的数学公式减少了迭代次数，使其的最坏计算复杂度和最小二乘法类似。

四、原理证明

Lasso回归代价函数为凸函数

同样需要证明：
$f\left(\frac{x_{1}+x_{2}}{2}\right) \leq \frac{f\left(x_{1}\right)+f\left(x_{2}\right)}{2}$

不等式左边：
$\operatorname{Cost}\left(\frac{w_{1}+w_{2}}{2}\right)=\sum_{i=1}^{N}\left[\left(\frac{w_{1}+w_{2}}{2}\right)^{T} x_{i}-y_{i}\right]^{2}+\lambda\left\|\frac{w_{1}+w_{2}}{2}\right\|_{1}$

不等式右边：
$\frac{\operatorname{Cost}\left(w_{1}\right)+\operatorname{Cost}\left(w_{2}\right)}{2}=\frac{\sum_{i=1}^{N}\left(w_{1}^{T} x_{i}-y_{i}\right)^{2}+\sum_{i=1}^{N}\left(w_{2}^{T} x_{i}-y_{i}\right)^{2}+\lambda\left\|w_{1}\right\|_{1}+\lambda\left\|w_{2}\right\|_{1}}{2}$

（1）不等式两边的前半部分与标准线性回归一致，只需要证明剩下的差值大于等于零即可
（2）根据向量范数的正齐次性，常数项系数可以乘进去
（3）将 λ 提到括号外
（4）根据向量范数的定义，满足三角不等式，必然是大于等于零
$\begin{aligned} \Delta &=\lambda\left\|w_{1}\right\|_{1}+\lambda\left\|w_{2}\right\|_{1}-2 \lambda\left\|\frac{w_{1}+w_{2}}{2}\right\|_{1} & (1) \\ &=\lambda\left\|w_{1}\right\|_{1}+\lambda\left\|w_{2}\right\|_{1}-\lambda\left\|w_{1}+w_{2}\right\|_{1} & (2) \\ &=\lambda\left(\left\|w_{1}\right\|_{1}+\left\|w_{2}\right\|_{1}-\left\|w_{1}+w_{2}\right\|_{1}\right) & (3) \\ & \geq 0 & (4) \end{aligned}$

人为的控制 λ 的大小，最后的结果在实数范围内必然大于等于零，证毕。

最小回归法数学公式

求单位角平分向量：

（1）设单位角平分向量为 $u_A$ ，可以将其看成选中的特征向量的线性组合，下标 A 表示选中的特征的序号集合
（2）由于每个选中的特征向量与角平分向量的夹角都相同，所以特征向量与角平分向量的点积后的向量每一个元素必然相同， $1_A$ 为元素都为 1 的向量，z 为常数
（3）根据（2）式可以表示出线性组合的系数向量 $ω_A$
$\begin{aligned} & u_\mathcal{A} = X_\mathcal{A} \omega_\mathcal{A} & (1)\\ & X_\mathcal{A}^Tu_\mathcal{A} = X_\mathcal{A}^TX_\mathcal{A} \omega_\mathcal{A} = z 1_\mathcal{A} & (2)\\ & \omega_\mathcal{A} = z(X_\mathcal{A}^TX_\mathcal{A})^{-1} 1_\mathcal{A} & (3) \end{aligned}$

（1）角平分向量 $u_A$ 为单位向量，所以长度为 1
（2）改写成向量的形式
（3）带入上一步的线性组合的系数向量 $ω_A$
（4）根据转置的性质第一项的括号可以化简，提出常数 z
（5）矩阵乘以其逆矩阵为单位矩阵，所以可以化简
（6）最后解得常数 z 的表达式
$\begin{aligned} & \left\|u_{\mathcal{A}}\right\|^{2}=1 & (1)\\ & \omega_{\mathcal{A}}^{T} X_{\mathcal{A}}^{T} X_{\mathcal{A}} \omega_{\mathcal{A}}=1 & (2) \\ & \left(z\left(X_{\mathcal{A}}^{T} X_{\mathcal{A}}\right)^{-1} 1_{\mathcal{A}}\right)^{T} X_{\mathcal{A}}^{T} X_{\mathcal{A}} z\left(X_{\mathcal{A}}^{T} X_{\mathcal{A}}\right)^{-1} 1_{\mathcal{A}}=1 & (3) \\ & z^{2} 1_{\mathcal{A}}^{T}\left(X_{\mathcal{A}}^{T} X_{\mathcal{A}}\right)^{-1}\left(X_{\mathcal{A}}^{T} X_{\mathcal{A}}\right)\left(X_{\mathcal{A}}^{T} X_{\mathcal{A}}\right)^{-1} 1_{\mathcal{A}}=1 & (4) \\ & z^21_\mathcal{A}^T\left(X_\mathcal{A}^TX_\mathcal{A}\right)^{-1}1_\mathcal{A} = 1 & (5) \\ & z= \frac{1}{\sqrt[]{1_\mathcal{A}^T\left(X_\mathcal{A}^TX_\mathcal{A}\right)^{-1}1_\mathcal{A}}} = \left(1_\mathcal{A}^T\left(X_\mathcal{A}^TX_\mathcal{A}\right)^{-1}1_\mathcal{A}\right)^{-\frac{1}{2} } & (6) \\ \end{aligned}$

（1）将特征向量的转置乘以特征向量用 $G_A$ 表示
（2）带入 $G_A$ ，得到 z 的表达式
（3）带入 $G_A$ ，得到 $ω_A$ 的表达式
$\begin{aligned}{} & G_{\mathcal{A}}=X_{\mathcal{A}}^{T} X_{\mathcal{A}} & (1)\\ & z=\left(1_{\mathcal{A}}^{T}\left(G_{\mathcal{A}}\right)^{-1} 1_{\mathcal{A}}\right)^{-\frac{1}{2}} & (2)\\ & \omega_{\mathcal{A}}=z\left(G_{\mathcal{A}}\right)^{-1} 1_{\mathcal{A}} & (3) \end{aligned}$

将 $X_A$ 乘以 $ω_A$ ，就得到了角平分向量 $u_A$ 的表达式，这样就可以求出单位角平分向量。更加详细的证明请参考 Bradley Efron 的论文⁴。

求角平分向量的长度：

（1） $μ_A$ 表示当前预测值，沿着角平分向量的方向更新一个 γ 长度
（2）C 表示特征向量与残差向量的相关性，为两个向量的点积，带入（1）式，得到相关性的更新表达式
（3）当特征向量为被选中的特征向量时，由于每个特征向量与角平分向量的乘积都相同，都等于 z
（4）计算每个特征向量与角平分向量的乘积
（5）当特征向量不是被选中的特征向量时，使用 a 来带入（2）式
（6）要想加入下一个特征向量，则（3）式与（5）式的绝对值必然相等，才能保证下一次更新后的相关性也是相同的
（7）解得 γ 的表达式
$\begin{aligned} &\mu_{A^{+}}=\mu_{A}+\gamma u_{A} & (1)\\ &C_{+}=X^{T}\left(y-\mu_{A^{+}}\right)=X^{T}\left(y-\mu_{A}-\gamma u_{A}\right)=C-\gamma X^{T} u_{A} & (2)\\ &C_{+}=C-\gamma z \quad(j \in A) & (3)\\ &a=X^{T} u_{A} & (4)\\ &C_{+}=C_{j}-\gamma a_{j} \quad(j \notin A) & (5)\\ &|C-\gamma z|=\left|C-\gamma a_{j}\right| & (6)\\ &\gamma=\min _{j \notin A}^{+}\left\{\frac{C-C_{j}}{z-a_{j}}, \frac{C+C_{j}}{z+a_{j}}\right\} & (7) \end{aligned}$

这样就求出了 γ 的表达式，也就是角平分向量的长度。更加详细的证明请参考 Bradley Efron 的论文⁴。

五、代码实现

使用 Python 实现Lasso回归算法（坐标下降法）：
注：本实现未考虑偏移量 b ，需要对特征进行归一化处理

def lassoUseCd(X, y, lambdas=0.1, max_iter=1000, tol=1e-4):
    """
    Lasso回归，使用坐标下降法（coordinate descent）
    args:
        X - 训练数据集
        y - 目标标签值
        lambdas - 惩罚项系数
        max_iter - 最大迭代次数
        tol - 变化量容忍值
    return:
        w - 权重系数
    """
    # 初始化 w 为零向量
    w = np.zeros(X.shape[1])
    for it in range(max_iter):
        done = True
        # 遍历所有自变量
        for i in range(0, len(w)):
            # 记录上一轮系数
            weight = w[i]
            # 求出当前条件下的最佳系数
            w[i] = down(X, y, w, i, lambdas)
            # 当其中一个系数变化量未到达其容忍值，继续循环
            if (np.abs(weight - w[i]) > tol):
                done = False
        # 所有系数都变化不大时，结束循环
        if (done):
            break
    return w

def down(X, y, w, index, lambdas=0.1):
    """
    cost(w) = (x1 * w1 + x2 * w2 + ... - y)^2 + ... + λ(|w1| + |w2| + ...)
    假设 w1 是变量，这时其他的值均为常数，带入上式后，其代价函数是关于 w1 的一元二次函数，可以写成下式：
    cost(w1) = (a * w1 + b)^2 + ... + λ|w1| + c (a,b,c,λ 均为常数)
    => 展开后
    cost(w1) = aa * w1^2 + 2ab * w1 + λ|w1| + c (aa,ab,c,λ 均为常数)
    """
    # 展开后的二次项的系数之和
    aa = 0
    # 展开后的一次项的系数之和
    ab = 0
    for i in range(X.shape[0]):
        # 括号内一次项的系数
        a = X[i][index]
        # 括号内常数项的系数
        b = X[i][:].dot(w) - a * w[index] - y[i]
        # 可以很容易的得到展开后的二次项的系数为括号内一次项的系数平方的和
        aa = aa + a * a
        # 可以很容易的得到展开后的一次项的系数为括号内一次项的系数乘以括号内常数项的和
        ab = ab + a * b
    # 由于是一元二次函数，当导数为零时，函数值最小值，只需要关注二次项系数、一次项系数和 λ
    return det(aa, ab, lambdas)

def det(aa, ab, lambdas=0.1):
    """
    通过代价函数的导数求 w，当 w = 0 时，不可导
    det(w) = 2aa * w + 2ab + λ = 0 (w > 0)
    => w = - (2 * ab + λ) / (2 * aa)

    det(w) = 2aa * w + 2ab - λ = 0 (w < 0)
    => w = - (2 * ab - λ) / (2 * aa)

    det(w) = NaN (w = 0)
    => w = 0
    """
    w = - (2 * ab + lambdas) / (2 * aa)
    if w < 0:
        w = - (2 * ab - lambdas) / (2 * aa)
        if w > 0:
            w = 0
    return w

使用 Python 实现Lasso回归算法（最小角回归法）：

def lassoUseLars(X, y, lambdas=0.1, max_iter=1000):
    """
    Lasso回归，使用最小角回归法（Least Angle Regression）
    论文：https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf
    args:
        X - 训练数据集
        y - 目标标签值
        lambdas - 惩罚项系数
        max_iter - 最大迭代次数
    return:
        w - 权重系数
    """
    n, m = X.shape
    # 已被选择的特征下标
    active_set = set()
    # 当前预测向量
    cur_pred = np.zeros((n,), dtype=np.float32)
    # 残差向量
    residual = y - cur_pred
    # 特征向量与残差向量的点积，即相关性
    cur_corr = X.T.dot(residual)
    # 选取相关性最大的下标
    j = np.argmax(np.abs(cur_corr), 0)
    # 将下标添加至已被选择的特征下标集合
    active_set.add(j)
    # 初始化权重系数
    w = np.zeros((m,), dtype=np.float32)
    # 记录上一次的权重系数
    prev_w = np.zeros((m,), dtype=np.float32)
    # 记录特征更新方向
    sign = np.zeros((m,), dtype=np.int32)
    sign[j] = 1
    # 平均相关性
    lambda_hat = None
    # 记录上一次平均相关性
    prev_lambda_hat = None
    for it in range(max_iter):
        # 计算残差向量
        residual = y - cur_pred
        # 特征向量与残差向量的点积
        cur_corr = X.T.dot(residual)
        # 当前相关性最大值
        largest_abs_correlation = np.abs(cur_corr).max()
        # 计算当前平均相关性
        lambda_hat = largest_abs_correlation / n
        # 当平均相关性小于λ时，提前结束迭代
        # https://github.com/scikit-learn/scikit-learn/blob/2beed55847ee70d363bdbfe14ee4401438fba057/sklearn/linear_model/_least_angle.py#L542
        if lambda_hat <= lambdas:
            if (it > 0 and lambda_hat != lambdas):
                ss = ((prev_lambda_hat - lambdas) / (prev_lambda_hat - lambda_hat))
                # 重新计算权重系数
                w[:] = prev_w + ss * (w - prev_w)
            break
        # 更新上一次平均相关性
        prev_lambda_hat = lambda_hat

        # 当全部特征都被选择，结束迭代
        if len(active_set) > m:
            break

        # 选中的特征向量
        X_a = X[:, list(active_set)]
        # 论文中 X_a 的计算公式 - (2.4)
        X_a *= sign[list(active_set)]
        # 论文中 G_a 的计算公式 - (2.5)
        G_a = X_a.T.dot(X_a)
        G_a_inv = np.linalg.inv(G_a)
        G_a_inv_red_cols = np.sum(G_a_inv, 1)     
        # 论文中 A_a 的计算公式 - (2.5)
        A_a = 1 / np.sqrt(np.sum(G_a_inv_red_cols))
        # 论文中 ω 的计算公式 - (2.6)
        omega = A_a * G_a_inv_red_cols
        # 论文中角平分向量的计算公式 - (2.6)
        equiangular = X_a.dot(omega)
        # 论文中 a 的计算公式 - (2.11)
        cos_angle = X.T.dot(equiangular)
        # 论文中的 γ
        gamma = None
        # 下一个选择的特征下标
        next_j = None
        # 下一个特征的方向
        next_sign = 0
        for j in range(m):
            if j in active_set:
                continue
            # 论文中 γ 的计算方法 - (2.13)
            v0 = (largest_abs_correlation - cur_corr[j]) / (A_a - cos_angle[j]).item()
            v1 = (largest_abs_correlation + cur_corr[j]) / (A_a + cos_angle[j]).item()
            if v0 > 0 and (gamma is None or v0 < gamma):
                gamma = v0
                next_j = j
                next_sign = 1
            if v1 > 0 and (gamma is None or v1 < gamma):
                gamma = v1
                next_j = j
                next_sign = -1
        if gamma is None:
            # 论文中 γ 的计算方法 - (2.21)
            gamma = largest_abs_correlation / A_a

        # 选中的特征向量
        sa = X_a
        # 角平分向量
        sb = equiangular * gamma
        # 解线性方程（sa * sx = sb）
        sx = np.linalg.lstsq(sa, sb)
        # 记录上一次的权重系数
        prev_w = w.copy()
        d_hat = np.zeros((m,), dtype=np.int32)
        for i, j in enumerate(active_set):
            # 更新当前的权重系数
            w[j] += sx[0][i] * sign[j]
            # 论文中 d_hat 的计算方法 - (3.3)
            d_hat[j] = omega[i] * sign[j]
        # 论文中 γ_j 的计算方法 - (3.4)
        gamma_hat = -w / d_hat
        # 论文中 γ_hat 的计算方法 - (3.5)
        gamma_hat_min = float("+inf")
        # 论文中 γ_hat 的下标
        gamma_hat_min_idx = None
        for i, j in enumerate(gamma_hat):
            if j <= 0:
                continue
            if gamma_hat_min > j:
                gamma_hat_min = j
                gamma_hat_min_idx = i
        if gamma_hat_min < gamma:
            # 更新当前预测向量 - (3.6)
            cur_pred = cur_pred + gamma_hat_min * equiangular
            # 将下标移除至已被选择的特征下标集合
            active_set.remove(gamma_hat_min_idx)
            # 更新特征更新方向集合
            sign[gamma_hat_min_idx] = 0
        else:
            # 更新当前预测向量
            cur_pred = X.dot(w)
            # 将下标添加至已被选择的特征下标集合
            active_set.add(next_j)
            # 更新特征更新方向集合
            sign[next_j] = next_sign

    return w

六、第三方库实现

scikit-learn⁶ 实现（坐标下降法）：

from sklearn.linear_model import Lasso

# 初始化Lasso回归器，默认使用坐标下降法
reg = Lasso(alpha=0.1, fit_intercept=False)
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_

scikit-learn⁷ 实现（最小角回归法）：

from sklearn.linear_model import LassoLars

# 初始化Lasso回归器，使用最小角回归法
reg = LassoLars(alpha=0.1, fit_intercept=False)
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_

七、示例演示

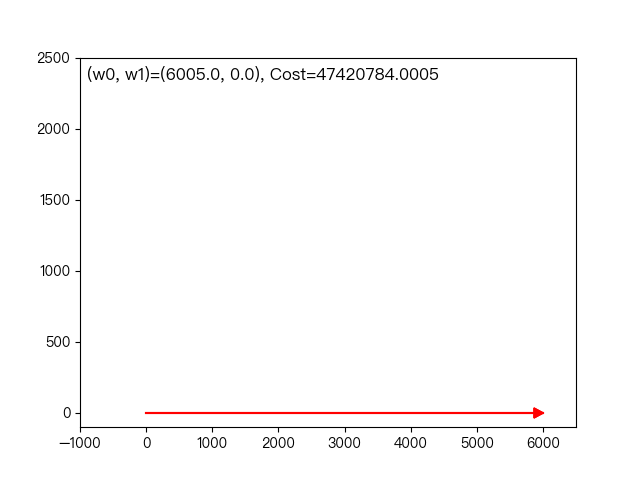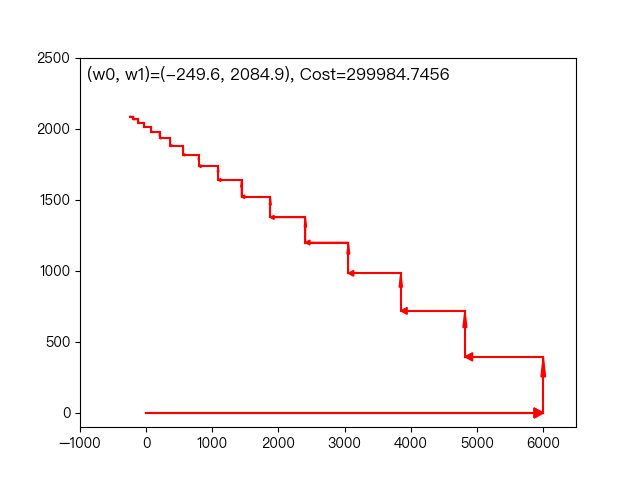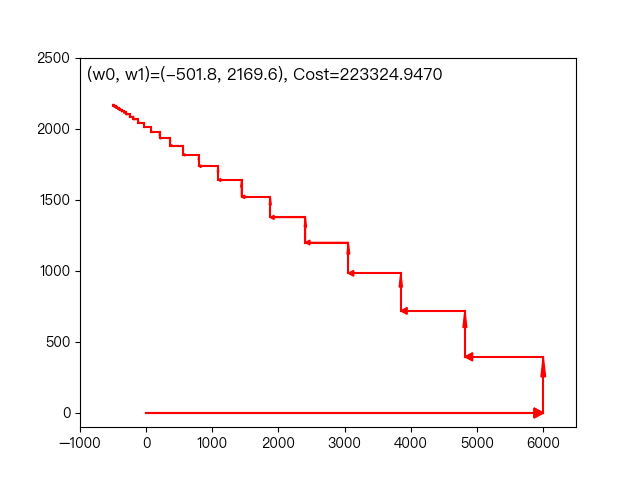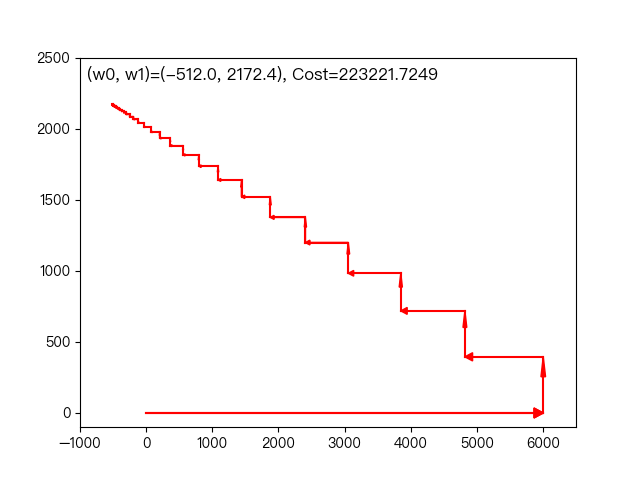
下面动图展示了前面一节的工作年限与平均月工资的例子，每次只朝这坐标轴的一个方向改变权重系数，逐渐逼近最优解的过程。

坐标下降法

下面动图展示了 λ 对各个自变量权重系数的影响，横轴为惩罚系数 λ ，纵轴为权重系数，每一个颜色表示一个自变量的权重系数（训练数据来源于sklearn diabetes datasets）：

λ 对权重系数的影响

可以看到当 λ 逐渐增大时（ λ 向左移动），某些特征的权重系数会快速变成零，通过这个性质说明Lasso 回归可以用来做特征选择，控制 λ 的大小来选择出关键特征。

八、思维导图

九、参考文献

https://en.wikipedia.org/wiki/Lasso_(statistics)
https://en.wikipedia.org/wiki/Coordinate_descent
https://en.wikipedia.org/wiki/Least-angle_regression
https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf
https://zhuanlan.zhihu.com/p/46999826
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LassoLars.html

完整演示请点击这里