【李宏毅机器学习2021】Task02 回归

【李宏毅机器学习2021】本系列是针对datawhale《李宏毅机器学习-2022 10月》的学习笔记。本次是对回归的学习总结。本节通过视频学习到回归任务的提出，三个要素，及如何优化。李老师通过层层递进，提出问题解决问题的方式不断打磨方法，从中介绍回归任务的始末，引出深度学习及网络加深伴随的过拟合问题。

目录

Task02 回归

不同的机器学习方程类型：

回归

分类

 structure learning

如何求得方程：

1.写出带有未知数的方程

 2.为训练数据定义损失函数

3.优化（Optimization）

模型优化：

1.增加para数据量，引入更多有效信息

2.更改模型

---

Task02 回归

书接上回，Machine Learning的本质就是让计算机找一个解决问题的方程。

不同的机器学习方程类型：

回归

例如给定一些特征，对数据进行预测。例如给定PM2.5相关的参数，如臭氧、今日的PM2.5、今日温度湿度等，预测明天的温度。

 

分类

给定特征，对数据进行分类。且分类的目标已经提前告诉计算机，让计算机做选择题。例如判断邮箱邮件是不是垃圾邮件。 

再比如告诉计算机棋盘的情况，让计算机下棋，计算机自己选择19*19矩阵内的一点。

 

 structure learning

分类回归只是一小部分，深度学习能做的还有很多很多！！！

如何求得方程：

 

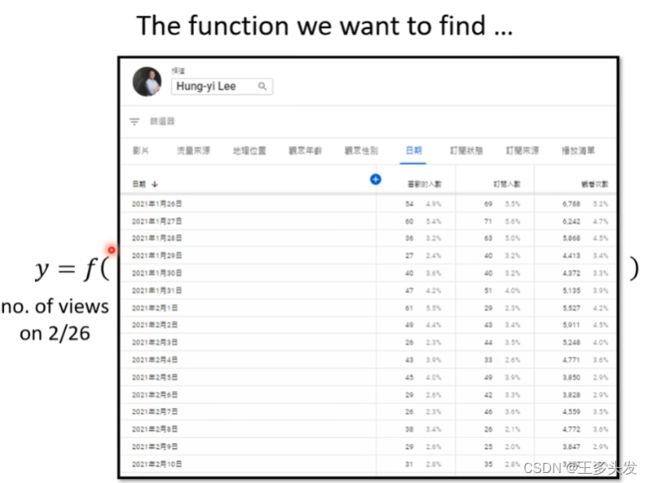
 在这里李老师给出了一个任务，就是给出历史的YouTuBe的视频播放量，预测明天视频播放量是多少。

这里的方程任务就是输入历史数据，输出预测情况（回归）。

1.写出带有未知数的方程

将输出和输出用函数表示联系起来，同时加入未知数w（权重）和b（偏值）。

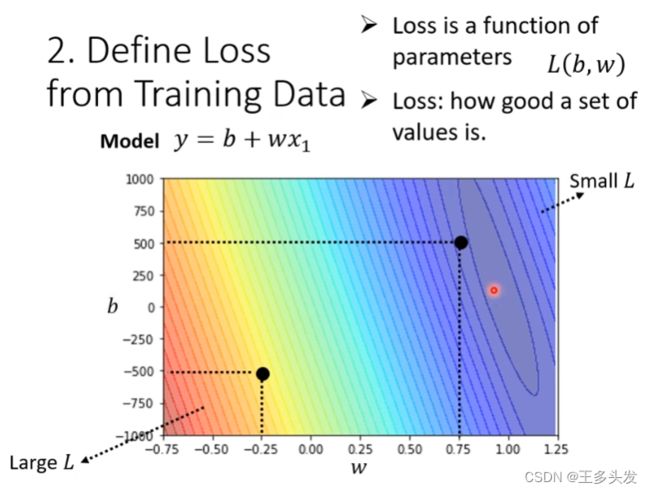
 2.为训练数据定义损失函数

 损失函数的出现是为了判断你在1中提出的方程有多好，例如通过你的预测在输入17年1月1日后预测2号的播放量为5.3K 实际播放量为4.9K  相差0.4K即为当前的loss。

两种loss： 

MAE 平均值loss

MSE 方差loss（作业里使用）

知道了怎么评价，下一个问题又来了。如何调整方程，让他更好的进行预测呢？

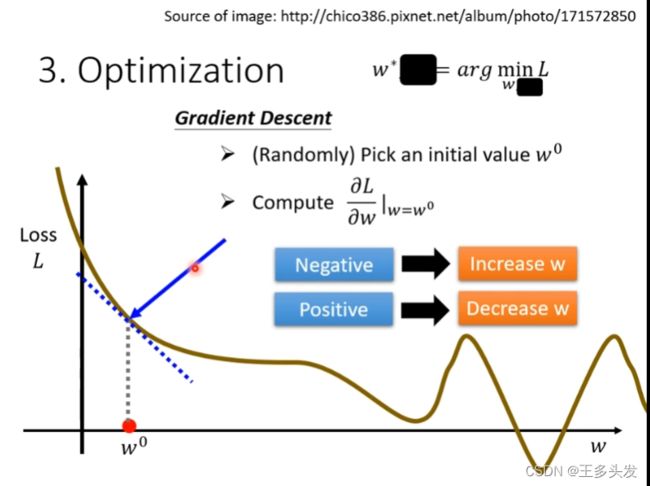
3.优化（Optimization）

采用梯度下降算法对提出的函数优化，让函数找到一个局部最优解。在向梯度下降的位置移动，找到梯度为零的点。

引入学习率的概念，学习率表示每次找到梯度下降方向后要移动的大小尺寸。 

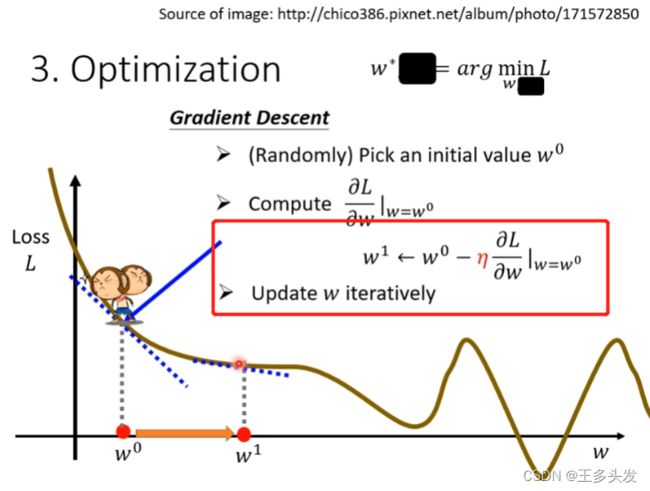
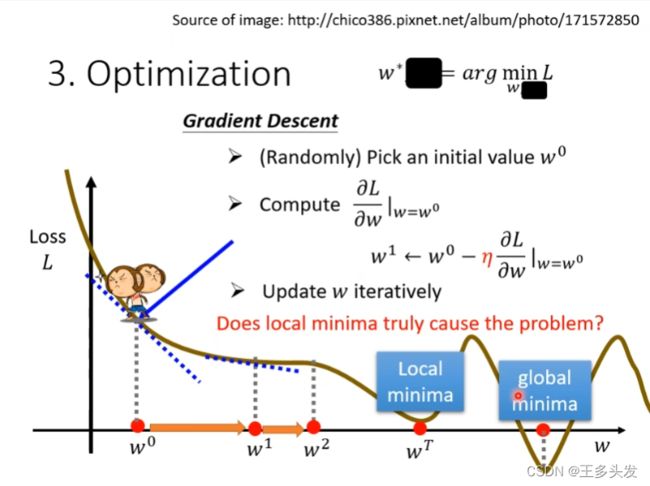
通过梯度下降的方法，对w参数不断优化，保证loss下降。函数找到合适的参数。 

 

这里又引出另一个问题，如果在local minima点梯度下降算法失效，会带来什么问题呢？一般来说局部最优解（local minima） 就可以解决问题了（在参数选择正态分布参数时）。而更严重的问题是过拟合问题。

在例子中梯度优化的步骤如上图。 

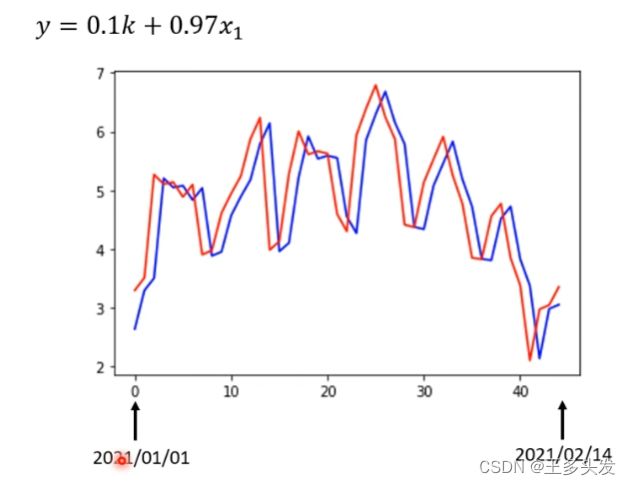
整体效果：

在经过上述三部操作后得到以下结果：

模型优化：

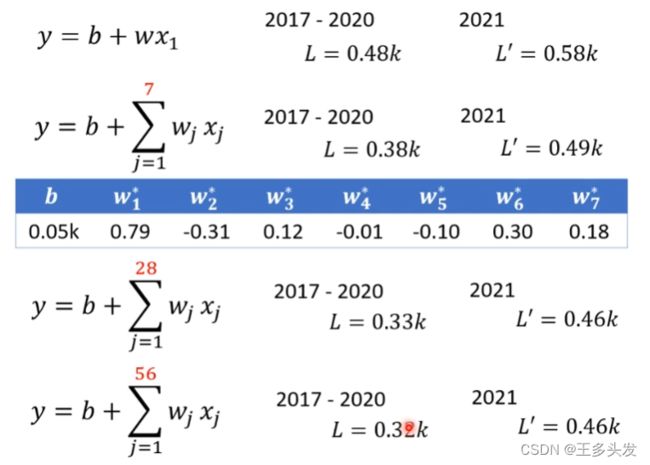
1.增加para数据量，引入更多有效信息

针对训练数据从一天的尺度不断扩充，从一天到七天，从七天到一个月、两个月。可以发现刚开始增加尺度还是有一定效果的，但是到后面增加数据也没了收益。

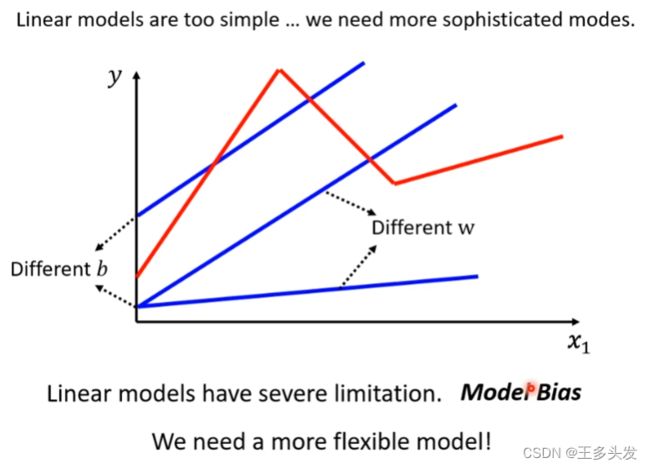
2.更改模型

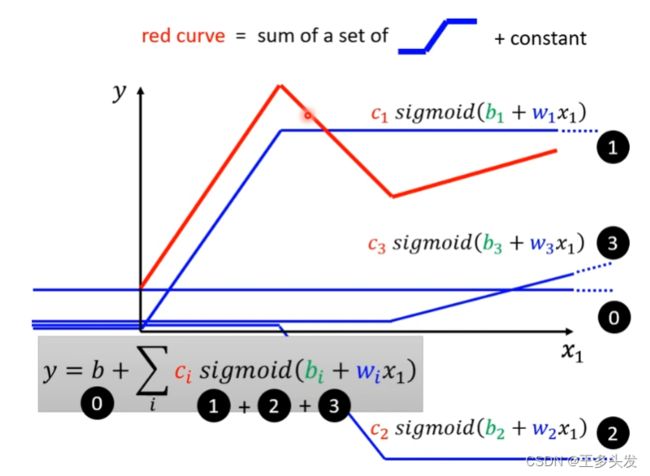
将模型更新成红色部分的函数，这样的函数进行预测应该有更好的效果。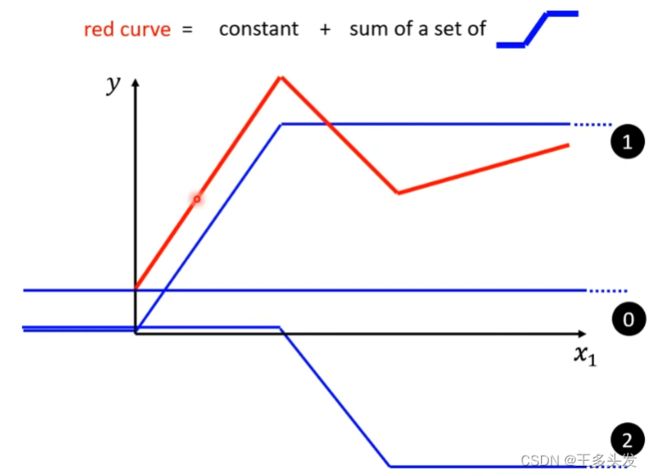 

 和傅里叶级数的概念差不多，一般函数常见函数（除了一些怪异的也不会在深度学习问题里出现）都可以用这样的分段函数去表示。他们的组合叠加，像傅里叶级数的信号叠加一样。

 

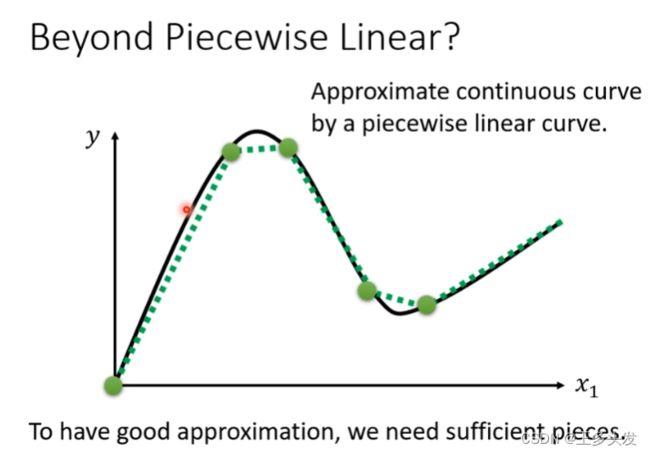
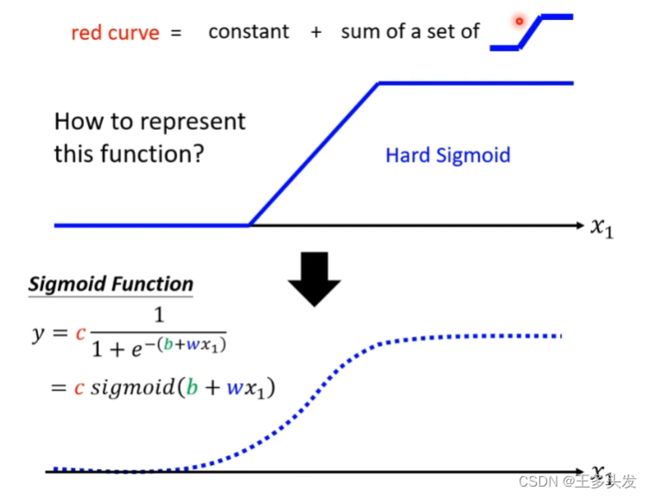
这里就会出现另一个问题，如何表示这样的折线函数呢？

Sigmoid函数

这里引入了sigmoid函数，去做分段函数。其实用这个Sigmoid函数的工作也是模拟了神经元，在输入信号达到一定值时，会做出反应，如果没有达到阈值反应比较微弱或没有反应。

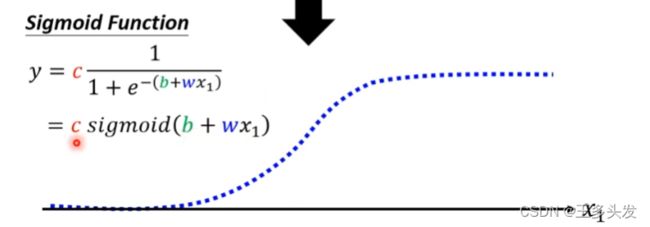
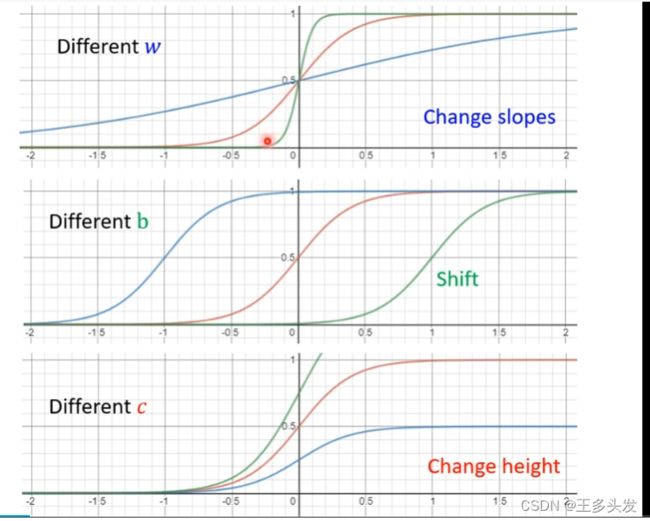
 通过采用不同的w和b及c可以调整sigmoid函数的表示，让他们综合起来可以表现任意函数。= =看起来就很像横过来的tanθ函数。

 

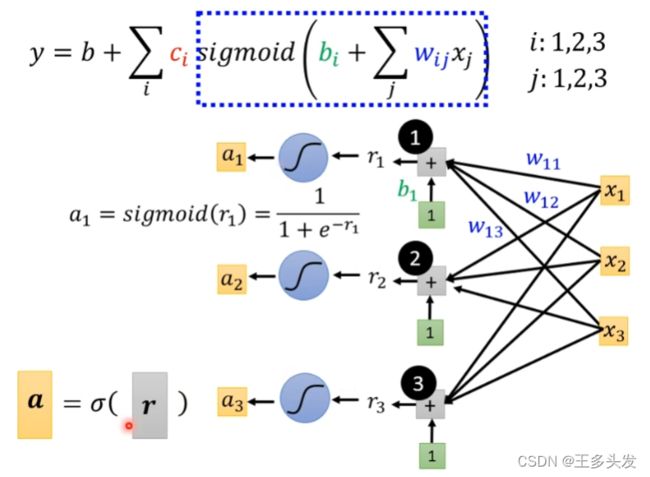
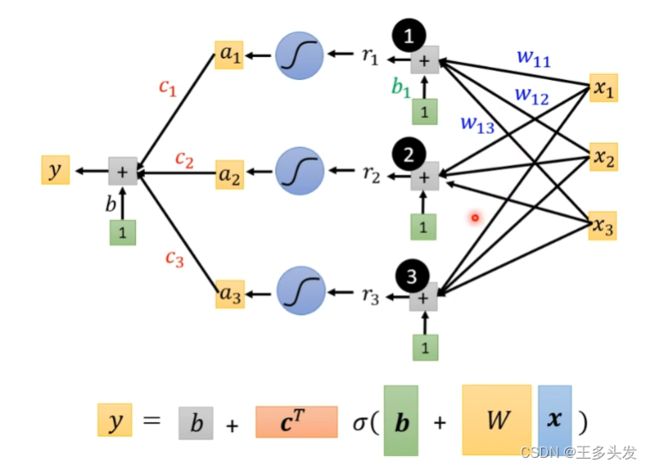
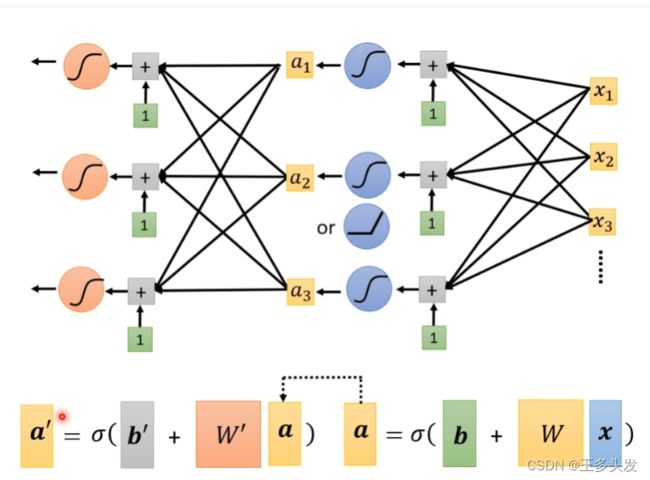
加入了sigmoid函数就复杂起来了，整体函数表现如下：

 

 看上去式子比较复杂，其实改改就很清晰了

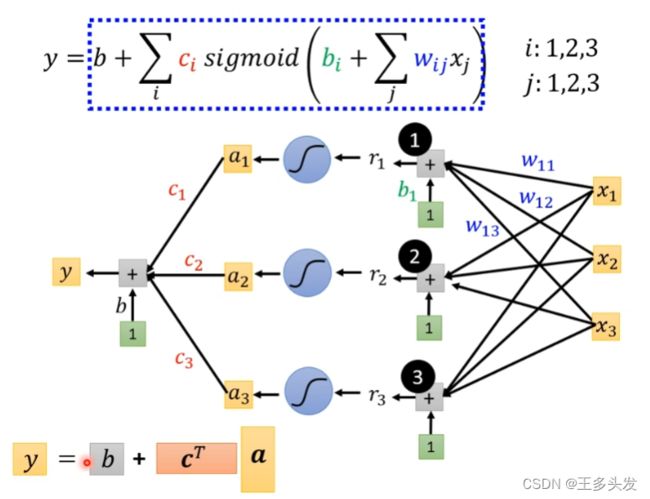
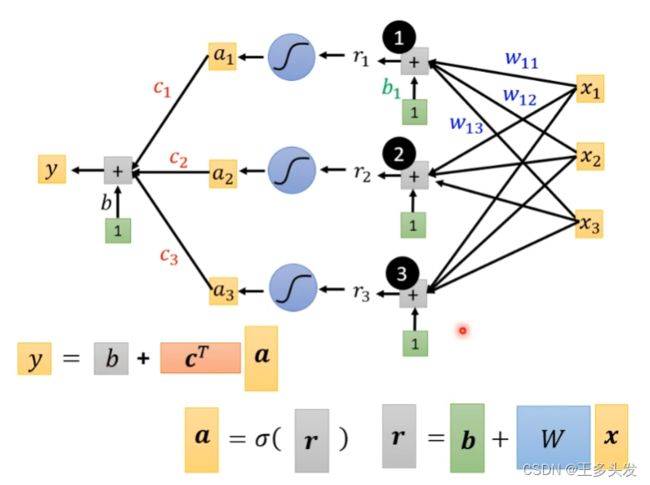
括号内的内容可以用r=b+wx矩阵形式表示。

 

 

  最终式子就如上所示。

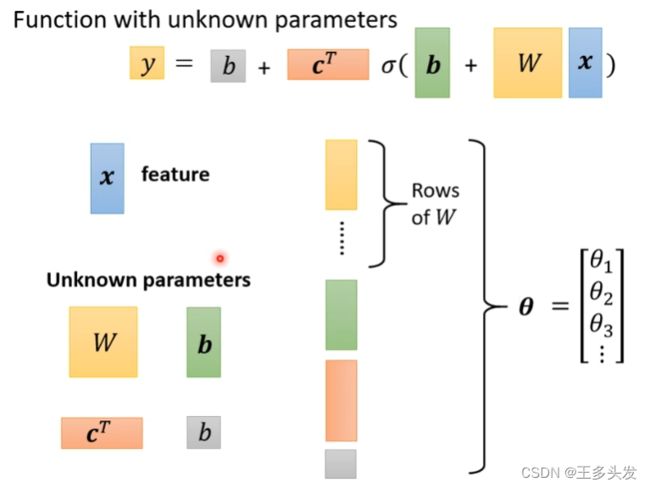
这里所有未知数都看作是θ

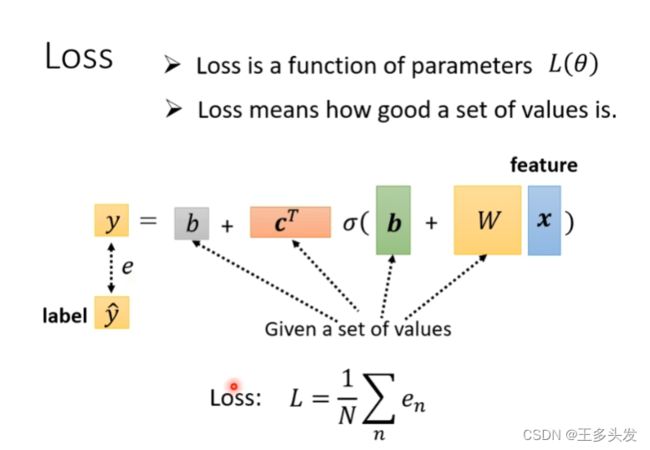
这里我们计算loss

 最后进行迭代优化

其实也一样，都差不多。

 

当然对每个数据做一次opt非常麻烦，这里对数据进行划分，每个batch优化一次loss。 

所以有数据集中数据都跑完叫一个epoch

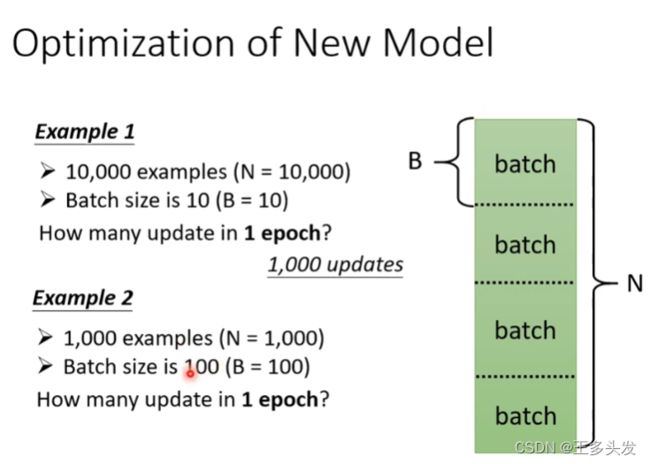 简单算一下:1000个数据 每个batch100个数据，这样就做十次opt

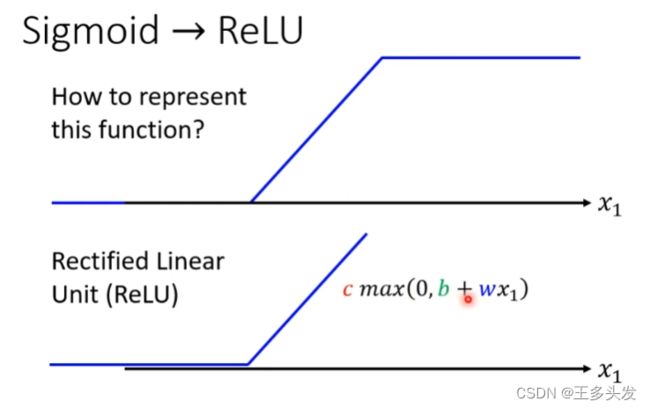
RELU

这里对sigmoid函数做优化调整，引入relu函数。

 

 

模型加深，进化成DeepLearning

 

 

这里表示很多网络叠加在一起，为什么要这样做，有什么好处呢？为什不横向加宽呢？

这里就买了一个包袱。

 这里盲目加深网络，会带来过拟合问题。over fitting 

 

最后让大家去猜如果用三层的，预测后天的结果会不会小于0.38。让大家真实感受一下预测的情况，我觉得大于0.38的概率大一些哈哈。 

【结语】本节课学习了深度学习的搭建方法，从一个线性预测一步步到神经网络再到深度学习模型。后面会跟着更新一个对作业的笔记。作业我也详细写一下笔记，虽然学过很多知识但是看完视频还是收获颇丰，继续加油吧~