深度学习基础——多层感知机

多层感知机（Multilayer Perceptron, MLP）是最简单的深度网络。本文回顾多层感知机的相关内容及一些基本概念术语。

多层感知机

为什么需要多层感知机

多层感知机是对线性回归的拓展和修正，可以看做是多层线性回归。因为线性回归中一般采用类似Softmax回归的模型结构，Softmax操作将输入直接映射到输出，虽然其本身非线性，但其仿射变换后输入输出为线性对应关系，即隐藏一个假设：输入输出之间具有单调线性关系，即特征的增大一定会导致模型输出的单调增大或减小。然而实际情况中，输入输出显然不一定具有单调性，而且特征之间相互会有影响，因此线性回归具有一定局限性。因此，我们引入深度神经网络。

什么是多层感知机

以输入、隐藏、输出三层感知机为例，由上节可知，多层感知机是为了克服线性回归的局限性而引入的。线性回归之所以会存在局限的原因是特征之间会有影响。因此我们可以在输入和输出之间虚拟一层作为”二次输入“（隐藏层）。隐藏层的值由输入层决定，通过线性回归的特性可知，隐藏层受输入层中的特征影响，而对于输出层，隐藏层又可以看做是新的输入层，是考虑了输入层特征之间影响而得到的输入层，因此，通过隐藏层的加入，三层感知机可以弥补单层线性回归的局限性。因为层与层间输入输出关系类似于人体交错纵横的神经元网络，所以称为神经网络。

需要注意的是，为了考虑所有特征之间的相互影响，最理想情况是每一层都考虑上一层之间所有特征之间相互影响的可能，即层与层之间为全连接结构。然而根据计算复杂度理论可知，全连接的神经网络的复杂度非常非常高，因此在实际使用中，存在实用性与有效性之间的权衡。

如何构建多层感知机

本节从数据角度推导如何建立多层感知机。用矩阵$\mathbf{X}\in {\mathbb{R}}^{n\times d}$表示$n$个样本的小批量，其中每个样本都有$d$个输入特征。为简单起见，此处推导单隐藏层的多层感知机，记其隐藏单元个数为$h$，$\mathbf{H}\in {\mathbb{R}}^{n\times h}$表示隐藏层的输出，称为隐藏表示（hidden representation）、隐藏层变量（hidden-layer variable）或者隐藏变量（hidden variable）。因为隐藏层和输出层都是全连接，所以有隐藏层权重${\mathbf{W}}^{(1)}\in {\mathbb{R}}^{n\times h}$ 和隐藏层偏置${\mathbf{b}}^{(1)}\in {\mathbb{R}}^{1\times h}$以及输出层权重${\mathbf{W}}^{(2)}\in {\mathbb{R}}^{h\times q}$和输出层偏置${\mathbf{b}}^{(2)}\in {\mathbb{R}}^{1\times q}$。

此时，可以计算出输出层的输出$\mathbf{O}\in {\mathbb{R}}^{n\times q}$为

$$\begin{gathered} \mathbf{H}=\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)} \\ \mathbf{O}=\mathbf{H}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)} \end{gathered}$$

接下来证明通过上式得到的输出与直接进行仿射变换得到的输出相等。联立以上两式，消掉隐藏层输出后可得

$$\begin{array}{rl}\mathbf{O}& =(\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)}){\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)}\\ & =\mathbf{X}{\mathbf{W}}^{(1)}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(1)}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)}\\ & =\mathbf{X}\mathbf{W}+\mathbf{b}\end{array}$$

通过以上证明可以，添加隐藏之后，模型的输入输出与线性回归相同，仍然遵循仿射变换关系！即添加的隐藏层没有任何作用！因此我们需要对隐藏层的输出进行处理，使其不再满足上式中的变换关系，我们采用的处理手段为激活函数（activation function），在隐藏层仿射变换后，对每个隐藏单元应用激活函数进行处理：

$$\begin{gathered} \mathbf{H}=\sigma (\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)}) \\ \mathbf{O}=\mathbf{H}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)} \end{gathered}$$

处理后的输出称为活性值（activations）。经过激活函数处理后，因为激活函数一般不满足仿射变换，所以处理后的多层感知机模型整体不再满足仿射变换关系。因为$\mathbf{X}$中的每一行对应一个样本，因此激活函数也按照行的方式作用于输入。

为了提升多层感知机的能力，可以继续堆叠这样的隐藏层，通过与上述过程类似的处理，可以产生效果更好的模型。

激活函数

通过上节的证明可以发现，多层感知机区别于线性回归的仿射变换的关键在于激活函数，激活函数一般是非线性的，通过计算加权和加上偏置来确定该神经元是否被激活，他可以将上一层的输入转换为可微分的输出，下面介绍常见的激活函数。

ReLU函数

ReLu是修正线性单元（Rectified linear unit，ReLu）的简称。对于任一给定元素$x$，ReLU函数为该元素与0的最大值，即函数可表示为

$$\mathbf{R}\mathbf{e}\mathbf{L}\mathbf{U}=max(x,0)$$

直观上看，ReLU函数将所有负元素的活性值设为0，从而将仿射变换变为非线性变换。而其导数对于负元素为0，正元素为1，即要么让特征保留，要么让特征消失，可以解决神经网络的梯度消失问题。

sigmoid函数

sigmoid函数的定义为对于任一定义域在$\mathbb{R}$的输入，可以将其变换为区间$(0,1)$之间的输出，因此sigmoid函数通常被称为挤压函数（squashing function）(将任意输入挤压到(0,1)之间)。

$$sigmoid(x)=\frac{1}{1+\exp (-x)}$$

从上式可看出，sigmoid的优点是平滑可微，然而其复杂度较高，因此常被用作输出单元的激活（隐藏层的激活用ReLu函数）。sigmoid函数的导数为

$$\frac{d}{dx}sigmoid(x)=\frac{exp(-x)}{(1+exp(-x){)}^2}=sigmoid(x)(1-sigmoid(x))$$

从导数可以看出，当$x\to 0^{-}$或$x\to 0^{+}$时，导数值趋近于0.25，$x\to +\infty$或$x\to -\infty$时，导数值趋向于0。通过画sigmoid函数的曲线图或者求二阶导数可以看出，函数在0附近接近线性0。

tanh函数

tanh（双曲正切）函数与sigmoid函数类似，也是将输入压缩到$(-1,1)$之间，不同的是，sigmoid函数关于原点中心对称。

$$\tanh (x)=\frac{1-\exp (-2x)}{1+\exp (-2x)}$$

其导数为

$$\frac{d}{dx}\tanh (x)=1-{\tanh }^2(x)$$

权重衰减

在训练过程中，过拟合是非常常见的现象，可以通过采用更多的训练数据来缓解过拟合，当数据数目难以增加时，可以采用正则化方法缓解过拟合，比如权重衰减。

权重衰减（weight decay）也被称为$L_2$正则化，通过函数与零的距离来衡量函数的复杂度。函数与零的距离可以采用范数来度量。对于线性函数$f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}$，可以采用其权重向量的范数来度量其与零的距离，即采用权重向量的范数可以度量函数复杂性，例如$\left | \mathbf{w} \right |^2 $。训练过程中，降低函数的复杂性，也就是要减小权重向量的范数，可以考虑将范数作为惩罚项加入到损失函数中，即原来的训练目标为最小化预测损失，现在改为最小化预测损失和惩罚项之和。

已有的线性函数的损失函数为：

$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}({\mathbf{w}}^T{\mathbf{x}}^{(i)}+b-y^{(i)}{)}^2$$

式中，${\mathbf{x}}^{(i)}$表示样本$i$的特征，$y^{(i)}$表示样本$i$的标签，$(\mathbf{w},b)$是权重和偏置参数。调整后，需要将权重向量的范数加入到损失函数中，具体如何添加来保持预测损失和权重向量范数的平衡未知，所以用常数$\lambda$来描述添加后的范数。为了消去求导后的常数系数，所以常数采用$\frac{\lambda }{2}$的形式。同样地，为了便于计算，采用平方范数进行度量而不是标准范数。易知，$\frac{\lambda }{2}$还是$\lambda$，采用平方范数还是标准范数对损失函数没有影响。添加后的损失函数为

$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}({\mathbf{w}}^T{\mathbf{x}}^{(i)}+b-y^{(i)}{)}^2+\frac{\lambda }{2}{\Vert \mathbf{w}\Vert }^2$$

当$\lambda$等于0时，损失函数没有变化。当$\lambda >0$时，可以对范数起到权衡作用。此外，选择$L_2$范数而不是$L_1$范数的原因是，$L_2$范数对权重向量的大分量施加了巨大的惩罚，这使得训练过程中偏向于大量特征上均匀分布权重的模型，相比之下，$L_1$范数会将权重集中于一小部分特征，将其他特征清除为0，因此适合于特征选择等场景。

暂退法

训练模型的目的是为了让模型能在未知的数据上获得较好的表现，即良好的泛化性。统计学中的泛化理论认为，为了模型在训练集和测试集上的性能差距，应该使模型尽可能简单。通过上节的讨论可知，模型的简单性可以通过范数来衡量，它是模型简单性的一种度量，模型的简单性还可以从其他角度度量，比如模型的平滑性，即模型不应对输入的微小变化敏感，如果给训练数据中添加随机噪声，对模型效果的影响应该是有限的。因此，可以考虑在训练有多层的深层网络时，向每一层注入噪声以增强输入输出映射上的平滑性。这种方法被称为暂退法（drop out）。

顾名思义，暂退法是在训练过程中做舍弃（drop out），在整个训练过程的每一次迭代中，将当前层中的一些节点置0。问题的关键在于如何添加这种随机噪声，噪声应满足何种特性。目前常用的一种噪声注入方式是以一种无偏向（unbiased）的方式注入噪声，即噪声满足均值为0的正态分布。这样在固定其他层时，每一层的期望等于不添加噪声的值。对于输入$\mathbf{x}$，在添加服从$ϵ\sim \mathcal{N}\left(0,{\sigma }^2\right)$的正态分布采样噪声后，产生扰动点${\mathbf{x}}^{\prime }=\mathbf{x}+ϵ$，扰动点的期望为$E[{\mathbf{x}}^{\prime }]=e[\mathbf{x}]$。

采用暂退法之后，如果要进行正则化，可以通过按照保留节点的分数进行规范化来进行。即，中间层的活性值$h$以暂退概率$p$替换为$h^{\prime }$。

$$h^{\prime }=\{\begin{array}{ll}0& \text{ 概率为 }p\\ \frac{h}{1-p}& \text{ 其他情况 }\end{array}$$

易知，此时的期望值仍保持不变，仍有$E[h^{\prime }]=h$成立。

需要注意的是，一般在测试时不用暂退法，也有特殊情况：在测试网络预测的不确定性时可以采用暂退法，如果不同的暂退法遮盖后得到的预测结构都一致，则网络较为稳定。

前向传播、反向传播、计算图

前向传播

本节以带权重衰减的单隐藏层多层感知机为例推导前向传播和反向传播。前向传播指的是按照从输入层到输出层的顺序计算和存储每层的结果。为简单起见，假设输入样本为$\mathbf{x}\in {\mathbb{R}}^d$，且隐藏层不包含偏置项（$b=0$）。中间变量为

$$\mathbf{z}={\mathbf{W}}^{(1)}\mathbf{x}$$

其中，${\mathbf{W}}^{(1)}\in {\mathbb{R}}^{h\times d}$是隐藏层的权重向量，隐藏层的中间变量经过激活函数$\varphi$之后，得到隐藏层长度为$h$的激活向量

$$\mathbf{h}=\varphi (\mathbf{z})$$

假设输出层的参数只有权重向量${\mathbf{W}}^{(2)}\in {\mathbb{R}}^{q\times h}$，则可以得到输出层变量，易知其是长度为$q$的向量

$$\mathbf{o}={\mathbf{W}}^{(2)}\mathbf{h}$$

记损失函数为$l$，样本标签为$y$，则可以得到单个样本的预测损失为

$$L=l(\mathbf{o},y)$$

因为此过程中有权重衰减，所以根据$L_2$正则化的定义，可以得出正则化项为

$$s=\frac{\lambda }{2}({\Vert {\mathbf{W}}^{(1)}\Vert }_F^2+{\Vert {\mathbf{W}}^{(2)}\Vert }_F^2)$$

则总的损失函数为

$$\mathbf{J}=L+s$$

因为训练目标是为了使损失最小，所以$\mathbf{J}$也被称为目标函数（objective function）。下图为与上述推导过程对应的数据流图，其中正方形为变量，圆圈表示操作符。

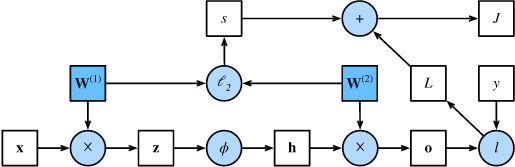
反向传播

反向传播（backward propagation）用于计算参数梯度。根据求导的连式法则，从输出层到输入层进行遍历，求取各参数的梯度。在上节的推导中，参数主要是隐藏层和输出层的权重向量${\mathbf{W}}^{(1)}$和${\mathbf{W}}^{(2)}$，反向传播的目的是计算梯度$\frac{\partial \mathbf{J}}{\partial {\mathbf{W}}^{(1)}}$和$\frac{\partial \mathbf{J}}{\partial {\mathbf{W}}^{(2)}}$。因此，根据连式法则，需要一次计算每个中间变量的参数和梯度，即按照计算图中数据流的反向进行计算，最终目标是求得两个权重变量的梯度。

从数据流图可以看出，第一步是计算目标函数分别相对于两项的梯度。易知其均为1，即

$$\begin{gathered} \frac{\partial \mathbf{J}}{\partial L}=1 \\ \frac{\partial \mathbf{J}}{\partial s}=1 \end{gathered}$$

第二步，求目标函数关于输出层输出$\mathbf{o}$的梯度

$$\frac{\partial \mathbf{J}}{\partial \mathbf{o}}=\frac{\partial \mathbf{J}}{\partial L}\cdot \frac{\partial L}{\partial \mathbf{o}}=\frac{\partial L}{\partial \mathbf{o}}\in {\mathbb{R}}^q$$

第三步，计算正则化项相对于相对于两个权重参数的梯度

$$\begin{gathered} \frac{\partial s}{\partial {\mathbf{W}}^{(1)}}=\lambda {\mathbf{W}}^{(1)} \\ \frac{\partial s}{\partial {\mathbf{W}}^{(2)}}=\lambda {\mathbf{W}}^{(2)}根据以上三部，可以计算出 \end{gathered}$$

根据以上三步，可以计算出最接近输出层的参数的梯度$\partial J/\partial {\mathbf{W}}^{(2)}\in {\mathbb{R}}^{q\times h}$

$$\frac{\partial J}{\partial {\mathbf{W}}^{(2)}}=\left(\frac{\partial J}{\partial \mathbf{o}}\cdot \frac{\partial \mathbf{o}}{\partial {\mathbf{W}}^{(2)}}\right)+\left(\frac{\partial J}{\partial s}\cdot \frac{\partial s}{\partial {\mathbf{W}}^{(2)}}\right)=\frac{\partial J}{\partial \mathbf{o}}{\mathbf{h}}^{\top }+\lambda {\mathbf{W}}^{(2)}$$

继续沿着数据流图求另一个参数，沿着输出层到隐藏层反向传播。关于隐藏层输出的梯度$\partial \mathbf{J}/\partial \mathbf{h}\in {\mathbb{R}}^h$可以根据下式计算

$$\frac{\partial J}{\partial \mathbf{h}}=\frac{\partial J}{\partial \mathbf{o}}\cdot \frac{\partial \mathbf{o}}{\partial \mathbf{h}}={\mathbf{W}}^{(2)}\frac{\partial J}{\partial \mathbf{o}}$$

因为激活函数$\varphi$的计算是以元素为单位的，所以计算中间变量$\mathbf{z}$的梯度$\partial \mathbf{J}/\partial \mathbf{z}\in {\mathbb{R}}^h$也需要艺元素为单位进行计算，我们用$\odot$表示按元素乘法

$$\frac{\partial J}{\partial \mathbf{z}}=\frac{\partial J}{\partial \mathbf{h}}\cdot \frac{\partial \mathbf{h}}{\partial \mathbf{z}}=\frac{\partial J}{\partial \mathbf{h}}\odot {\varphi }^{\prime }(\mathbf{z})$$

最后，可以得出最接近输入层的参数的梯度$\partial J/\partial {\mathbf{W}}^{(1)}\in {\mathbb{R}}^{h\times d}$

$$\frac{\partial J}{\partial {\mathbf{W}}^{(1)}}=\frac{\partial J}{\partial \mathbf{z}}\cdot \frac{\partial \mathbf{z}}{\partial {\mathbf{W}}^{(1)}}+\frac{\partial J}{\partial s}\cdot \frac{\partial s}{\partial {\mathbf{W}}^{(1)}}=\frac{\partial J}{\partial \mathbf{z}}{\mathbf{x}}^{\top }+\lambda {\mathbf{W}}^{(1)}$$

训练时，前向传播和反向传播相互依赖。前向传播时，沿着计算图正向计算所有变量，反向传播时计算这些变量对应的梯度。因此，训练时初始化模型参数后，需要交替进行前向传播和反向传播，利用反向传播给出的梯度来更新模型参数。需要注意的是，反向传播需要重复利用中间值，为了避免重复计算，需要将中间值进行存储直至反向传播完成，因此训练比单纯的预测需要消耗更多的内存，而且中间值的大小与网络层的数量和批量大小成正相关，因此，使用更大批量训练更深层次的网络要注意是否存在内存不足的问题。

数值稳定性和模型初始化

上文中主要关注的是在给定初始化模型参数的情况下，方案如何进行训练，对于如何给定初始化模型参数并未提及。然而，初始化模型参数及激活函数的选择对于方案的训练效果起到决定性作用。

此处讨论一个具有$L$层、输入为$\mathbf{x}$，输出$\mathbf{o}$的深层网络。每一层$l$由变换$f_l$定义，权重参数为${\mathbf{W}}^{(\mathbf{l})}$，隐藏变量为${\mathbf{h}}^{(1)}({\mathbf{h}}^{(0)}=\mathbf{x})$。根据上文推导易知，存在如下关系

$$\begin{gathered} {\mathbf{h}}^{(l)}=f_l({\mathbf{h}}^{(l-1)}) \\ \mathbf{o}=f_L\cdot ...\cdot f_1(\mathbf{x}) \end{gathered}$$

输出$\mathbf{o}$关于任一组权重参数${\mathbf{W}}^{(\mathbf{l})}$的梯度可以写为下式

$${\partial }_{{\mathbf{W}}^{(l)}0}=\underset{{\mathbf{M}}^{(L)\text{ def }}}{{\partial }_{{\mathbf{h}}^{(L-1}{\mathbf{h}}^{(L)}}}\cdot \dots \cdot \underset{{\mathbf{M}}^{(l+1)\text{ def }}}{{\partial }_{{\mathbf{h}}^{(l)}{\mathbf{h}}^{(l+1)}}}\underset{{\mathbf{v}}^{(l)\text{ def }}}{{\partial }_{\mathbf{W}}^{(l){\mathbf{h}}^{(l)}}}$$

可以看出，该梯度是$L-l$个矩阵${\mathbf{M}}^{(L)}\cdot ...\cdot {\mathbf{M}}^{(l+1)}$与梯度向量${\mathbf{v}}^{(l)}$的乘积。容易产生数值溢出的问题。在处理概率时，一种常用手段是取对数，将其映射到对数空间，可以将数据溢出的压力从尾数转移至指数，从而达到缓解压力的目的。然而，如果对上式进行这种操作，并不能起到缓解压力的作用甚至可能会加重。因为矩阵中可能有各种特征值，他们可能很大可能很小，他们的乘积可能很大也可能很小，导致映射到对数空间后仍有溢出的可能。

提不稳定一方面容易导致数值表示不正确，另一方面也会破坏算法的稳定性。如果梯度过大，会产生梯度爆炸（gradient exploding）的问题，使模型无法稳定收敛，要么会有梯度消失（gradient vanishing）的问题，是模型无法更新参数，无法学习。

常用的激活函数中，易知sigmoid函数在输入较大或较小时梯度变化很小甚至消失，因此使用sigmoid函数会导致梯度消失的现象，所以，ReLU更常用。

除了梯度消失和梯度爆炸的问题外，神经网络设计的另一个问题是其参数固有的对称性。如果对隐藏层的权重向量进行冲排列，同时对输出层的权重向量进行重排列，两种情况得出的函数相同，也就是说，每层的隐藏单元之间具有排列对称性。

环节排列对称性的一种方法是进行参数初始化。一般情况，默认的初始化权重向量为服从正态分布的权重值，因为正态分布更为适合一般情况的参数分布，一般情况下，这种方法较为有效。特殊情况下，可以采用Xavier参数初始化方法。

上文讨论的是线性全连接层输出，如果对于没有非线性的情况，该层$n_{in}$的输入$x_j$及相关权重可以由下式给出

$$o_i=\sum _{j=1}^{n_{in}}{w}_{ij}{x}_j$$

所有的权重为独立同分布，记该分布的均值为0，方差为${\sigma }^2$（并不意味着是正态分布）。假设输入$x_j$，输入之间相互独立且与权重独立同分布，记其方差为${\gamma }^2$（均值为0）。则可通过下式计算输出$o_i$的平均值和方差

$$\begin{array}{rl}E\left[o_i\right]& =\sum _{j=1}^{n_{\text{in }}}E\left[w_{ij}{x}_j\right]\\ & =\sum _{j=1}^{n_{\text{in }}}E\left[w_{ij}\right]E\left[x_j\right]\\ & =0\end{array}$$$$\begin{array}{rl}\mathrm{Var}\left[o_i\right]& =E\left[o_i^2\right]-{\left(E\left[o_i\right]\right)}^2\\ & =\sum _{j=1}^{n_{\text{in }}}E\left[w_{ij}^2{x}_j^2\right]-0\\ & =\sum _{j=1}^{n_{\text{in }}}E\left[w_{ij}^2\right]E\left[x_j^2\right]\\ & =n_{\text{in }}{\sigma }^2{\gamma }^2\end{array}$$

如果要保持方差不变，可以设置$n_{in}{\sigma }^2=1$。在反向传播过程中，通过推导可知，梯度的方差$Var[\partial wo]=n_{out}{\sigma }^2{\gamma }^2$。与输出的方差相似，除非有$n_{out}{\sigma }^2=1$，否则梯度的方差可能会增大导致平稳受到影响。易知以上两式无法同时满足，我们可以退而求其次，只需满足

$$\frac{1}{2}\left(n_{\text{in }}+n_{\text{out }}\right){\sigma }^2=1\text{ 或等价于 }\sigma =\sqrt{\frac{2}{n_{\text{in }}+n_{\text{out }}}}\text{. }$$

这就是Xavier参数初始化方法，从均值为0，方差${\sigma }^2=\frac{2}{n_{in}+n_{out}}$的正态分布中采样初始化参数。

环境和分布偏移

实际应用中，一般将模型训练好之后部署到实际应用场景中，然而如果实际数据分布改变，可能会导致模型效果大副下降，本节讨论数据分布可能变化的方式以及如何挽救模型性能。数据分布改变常常表现为数据分布偏移。常见的数据偏移方式包括协变量偏移、标签偏移、概念偏移等。

协变量偏移及纠正

协变量偏移指的是输入的分布随时间改变，标签函数（即条件分布$P(y|x)$）没有改变。

根据推导可知，如果不考虑正则化，可以用$\underset{f}{\mathrm{minimize}}\frac{1}{n}{\sum }_{i=1}^{n}l\left(f\left({\mathbf{x}}_i\right),y_i\right)$表示训练损失，其中$l$为损失函数，统计学中称此项为经验风险（empirical risk），用于近似真实风险（true risk），真实风险为从真实分布$p(x,y)$中抽取的所有数据总体损失的期望

$$E_{p(\mathbf{x},y)}[l(f(\mathbf{x}),y)]=\iint l(f(\mathbf{x}),y)p(\mathbf{x},y)d\mathbf{x}dy$$

然而，无法获得全部数据，因此，风险最小化指的是最小化经验风险。对于带标签的数据$(x_i,y_i)$，要评估$P(y|x)$。然而协变量偏移的情况下，观测值$x_i$是从源分布$q(x)$得出的，目标分布为$p(x)$。根据依赖性假设，即条件分布保持不变$p(y|x)=q(y|x)$。协变量偏移情况下，源分布发生了偏移，可以采用如下恒等式进行纠正

$$\iint l(f(\mathbf{x}),y)p(y\mid \mathbf{x})p(\mathbf{x})d\mathbf{x}dy=\iint l(f(\mathbf{x}),y)q(y\mid \mathbf{x})q(\mathbf{x})\frac{p(\mathbf{x})}{q(\mathbf{x})}d\mathbf{x}dy$$

即需要知道，数据来自正确分布与错误分布的概率之比，以此重新衡量每个样本的权重

$${\beta }_i\stackrel{\text{ def }}{=}\frac{p\left({\mathbf{x}}_i\right)}{q\left({\mathbf{x}}_i\right)}$$

将权重${\beta }_i$带入数据样本中，则此时可以使用”加权经验风险最小化“来训练模型

$$\underset{f}{\mathrm{minimize}}\frac{1}{n}\sum _{i=1}^n{\beta }_{i}l\left(f\left(\mathbf{x}\ast i\right),y\ast i\right)$$

但是，因为权重未知，因此需要对权重进行估计。可以采用的方法有很多，不过任意一种方法都需要从两个分布中抽取样本：从测试数据中获取”真实“分布$p$，从训练集中获取$q$。从恒等式可以知道，我们只需要$x\sim p(x)$和$x\sim q(x)$，因此只需要访问特征而不需要访问标签。

综上所述，需要对从两种分布中抽取的数据进行区分。可以很好区分的样本，其权重应该相应地显著增加或减少。如果两个分布无法区分，表明相关的样本可能来自两个分布的任意一个。

假设从$p(x)$和$q(x)$中抽取相同数量的样本，均用标签$z$表示，从$p$中抽取的标签为1，从$q$中抽取的标签为-1。则混合数据集的概率分布可以由下式给出

$$P(z=1\mid \mathbf{x})=\frac{p(\mathbf{x})}{p(\mathbf{x})+q(\mathbf{x})}\text{ and hence }\frac{P(z=1\mid \mathbf{x})}{P(z=-1\mid \mathbf{x})}=\frac{p(\mathbf{x})}{q(\mathbf{x})}$$

此时，可以采用对数几率回归（logistic regression，用于二元分类的softmax回归的特例），即对权重取对数,将其结果记为$h$。

$$log{\beta }_i\stackrel{\text{ def }}{=}log\frac{p\left({\mathbf{x}}_i\right)}{q\left({\mathbf{x}}_i\right)}=h$$

则可推出

$$\frac{p(x)}{q(x)}=exp(-h)$$

带入混合数据集的概率分布可得

$$P(z=1\mid \mathbf{x})=\frac{1}{1+\exp (-h(\mathbf{x}))}$$

至此，可以得出纠正协变量偏移的算法。假设训练集为$(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$和一个未标记的测试集$u_1,u_2,...,u_n$。$x_i,1\le i\le n$来自源分布，$u_i$来自目标分布。

1. 生成一个二元分类训练集$(x_1,-1),...,(x_n,-1),(u_1,1),...,(u_n,1)$

2. 用对数几率回归训练二元分类器得到函数$h$

3. 用${\beta }_i=exp(h(x_i))$或者${\beta }_i=min(exp(h(x_i)),c)(c为常量)$对训练数据进行加权

4. 使用权重${\beta }_i$进行训练

需要注意的是目标分布（测试分布）中不能存在训练时出现概率为0的样本，否则，会出现$p(x)>0$但$q(x)=0$的情况，其对应的权重为$\infty$。

标签偏移及纠正

标签偏移描述的问题与协变量偏移相反，$P(y)$改变但$P(x|y)$保持不变。

为了讨论方便，此处基本假设与协变量偏移的情况相同，所不同的是此时处理的是$k$个类别的分类问题，且标签的分布随时间变化，即$q(y)\ne p(y)$，但类别条件分布保持不变，即$p(x|y)=q(x|y)$。如果源分布出错，可以通过以下恒等式进行纠正

$$\iint l(f(\mathbf{x}),y)p(\mathbf{x}\mid y)p(y)d\mathbf{x}dy=\iint l(f(\mathbf{x}),y)q(\mathbf{x}\mid y)q(y)\frac{p(y)}{q(y)}d\mathbf{x}dy$$

类似地，权重应为

$${\beta }_i\stackrel{\text{ def }}{=}\frac{p\left({\mathbf{y}}_i\right)}{q\left({\mathbf{y}}_i\right)}$$

标签偏移时不改变$p(x)$，所以如果在源分布上得到一个模型，可以从中得出对权重的一致估计，而不需要处理其他维度。因此我们在训练集训练分类器，使用验证集计算其混淆矩阵。如果我们的分类器一开始就相当准确， 并且目标数据只包含我们以前见过的类别， 以及如果标签偏移假设成立（这里最强的假设）， 我们就可以通过求解一个简单的线性系统来估计测试集的标签分布$p(y)$。观测源数据上的标签，很容易估计分布$q(y)$，可以进一步求得权重，带入加权经验风险最小化。

概念偏移及纠正

概念偏移是指标签的定义发生变化，例如不同语境下对于同一个单词take的翻译不同、不同地区对于毒品的种类定义不同等。

概念偏移很难用原则性的方式解决，除了从零开始收集标签和训练目前别无他法。不过因为通常情况下，概念的变化总是相对缓慢的，因此，可以使用新数据更新现有的权重，而不是从头开始训练