卡尔曼滤波的统计学推导
卡尔曼滤波的统计学推导
本篇基于徐益达的机器学习——卡尔曼滤波详解介绍一下卡尔曼滤波的统计学公式推导。
1.背景知识
在介绍卡尔曼滤波之前必须知道的概念:
- 均方误差: E ( Δ 2 ) = ∑ p i ( l i − L ) 2 E(\Delta^2)=\sum{p_i(l_i-L)^2} E(Δ2)=∑pi(li−L)2
- 方差: σ 2 = E [ ( x − μ ) ( x − μ ) T ] \sigma^2=E[(x-\mu)(x-\mu)^T] σ2=E[(x−μ)(x−μ)T]
- 协方差: c o v ( X , Y ) = E [ ( X − μ ) ( Y − v ) T ] cov(X,Y)=E[(X-\mu)(Y-v)^T] cov(X,Y)=E[(X−μ)(Y−v)T]
- 高斯分布: 一 元 高 斯 分 布 X N ( μ , σ 2 ) 一元高斯分布 X~N(\mu,\sigma^2) 一元高斯分布X N(μ,σ2) f ( x ) = 1 σ 2 π e − ( x − μ ) ( x − μ ) T 2 σ 2 f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)(x-\mu)^T}{2\sigma^2}} f(x)=σ2π1e−2σ2(x−μ)(x−μ)T
2.公式推导
2.1 什么是动态模型?
如下图所示,每个时刻对应的观测值yi之间不是相互独立的。即这一时刻的观测值由之前时刻的观测值决定。但是在动态模型中,我们往往不求解观测值之间的相互影响关系,而是对应每个时刻观测值寻找一个隐状态xi,通过求解隐状态之间相互影响的概率和隐状态与其观测值之间的影响概率去描述观测值之间的影响概率。
上图中Xi之间的蓝色箭头对应的概率叫作Transition Probability,是指隐状态之间的影响概率,用 P ( X t ∣ X t − 1 ) P(X_t|X_{t-1}) P(Xt∣Xt−1)表示。
白色的箭头对应的概率叫作 Measurement Probability,是指隐状态与观测值之间的影响概率,用 P ( Y t ∣ X t ) P(Y_t|X_t) P(Yt∣Xt)表示。
另外,该模型还需要另外一个初始概率,也叫先验概率Initial Probability。
当所有这样的概率都知道的时候,我们便可以描述任意一个动态模型了。
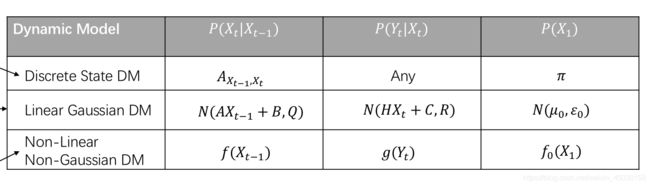
常见的几种动态模型如上表所示,表中给出了常见动态模型的Trasition probability 、 Measurement Probability 以及 initial probability。
第一种为离散状态的动态模型,典型代表为我们熟知的HMM(隐含马尔可夫)模型。离散状态主要是针对于Transition probability而言的,此概率可以用一个二维矩阵描述。而对于Measurement Probability 和 initial probability 而言 则没有过多的要求。
第二种为线性高斯模型。就是我们今天所说的卡尔曼滤波模型。他的三个概率就是一个带有高斯噪声的线性模型。
第三种为非线性非高斯模型。就是我们熟知的粒子滤波模型。他的三种概率仅需不是线性的不是高斯的任意函数均可。
2.2 卡尔曼滤波
滤波的目的: P ( x t ∣ y 1 , y 2 , . . . , y t ) P(x_t|y_1,y_2,...,y_t) P(xt∣y1,y2,...,yt)
将表格中的卡尔曼滤波具体化为如下: N ( A X t − 1 + B , Q ) − > X t = A X t − 1 + B + w w ∼ N ( 0 , Q ) N(AX_{t-1}+B,Q)->X_t=AX_{t-1}+B+w w\sim N(0,Q) N(AXt−1+B,Q)−>Xt=AXt−1+B+ww∼N(0,Q) N ( H X t + C , R ) − > y t = H X t + C + v v ∼ N ( 0 , R ) N(HX_t+C,R)->y_t=HX_t+C+v v\sim N(0,R) N(HXt+C,R)−>yt=HXt+C+vv∼N(0,R)
在这个模型中我们需要学习的参数如下 L . D M = [ A , B , Q , H , C , R ] L.DM=[A,B,Q,H,C,R] L.DM=[A,B,Q,H,C,R]
而在这里我们不讨论如何学习这些参数,我们只讨论参数的制定。
用一个例子去说明
假设有一个一维运动的小车,加速度服从0均值方差为v的高斯分布。
在这个例子中观测值y就是每个时刻我们观测到的小车的实际位置。而状态x如下表示: X = [ X t X t ˙ ] X=\begin{bmatrix} X_t \\ \dot{X_t} \end{bmatrix} X=[XtXt˙]
根据高中物理知识,卡尔曼滤波的两个方程可以写为: X t = X t − 1 + X ˙ t − 1 Δ t + 1 2 a ( Δ t ) 2 X_t=X_{t-1}+\dot{X}_{t-1}\Delta{t}+\frac{1}{2}a(\Delta{t})^2 Xt=Xt−1+X˙t−1Δt+21a(Δt)2
X ˙ t = X ˙ t − 1 + a Δ t \dot{X}_t=\dot{X}_{t-1}+a\Delta{t} X˙t=X˙t−1+aΔt
用矩阵的形式:
[ X t X t ˙ ] = [ 1 Δ t 0 1 ] [ X t − 1 X ˙ t − 1 ] + [ 1 2 a ( Δ t ) 2 a Δ t ] \begin{bmatrix} X_t \\ \dot{X_t} \end{bmatrix}=\begin{bmatrix} 1 & \Delta{t} \\ 0 & 1 \end{bmatrix} \begin{bmatrix} X_{t-1} \\ \dot{X}_{t-1} \end{bmatrix} + \begin{bmatrix} \frac{1}{2}a(\Delta{t})^2 \\ a\Delta{t} \end{bmatrix} [XtXt˙]=[10Δt1][Xt−1X˙t−1]+[21a(Δt)2aΔt]
等号坐边即为t时刻的状态。求其均值为右边第一项,方差计算如下: v a r ( X t ˉ ) = E [ ( X t ˉ − μ ) ( X t ˉ − μ ) T ] = E ( [ 1 2 a ( Δ t ) 2 a Δ t ] [ 1 2 a ( Δ t ) 2 a Δ t ] ) var(\bar{X_t})=E[(\bar{X_t}-\mu)(\bar{X_t}-\mu)^T]=E(\begin{bmatrix} \frac{1}{2}a(\Delta{t})^2 \\ a\Delta{t} \end{bmatrix} \begin{bmatrix} \frac{1}{2}a(\Delta{t})^2 \\ a\Delta{t} \end{bmatrix}) var(Xtˉ)=E[(Xtˉ−μ)(Xtˉ−μ)T]=E([21a(Δt)2aΔt][21a(Δt)2aΔt])
= E ( [ 1 4 a 2 ( Δ t ) 4 1 2 a 2 ( Δ t ) 3 1 2 a 2 ( Δ t ) 3 a 2 ( Δ t ) 2 ] = E ( a 2 ) [ 1 4 ( Δ t ) 4 1 2 ( Δ t ) 3 1 2 ( Δ t ) 3 ( Δ t ) 2 ] =E(\begin{bmatrix} \frac{1}{4}a^2(\Delta{t})^4 & \frac{1}{2}a^2(\Delta{t})^3 \\ \frac{1}{2}a^2(\Delta{t})^3 & a^2(\Delta{t})^2 \end{bmatrix}=E(a^2)\begin{bmatrix} \frac{1}{4}(\Delta{t})^4 & \frac{1}{2}(\Delta{t})^3 \\ \frac{1}{2}(\Delta{t})^3 & (\Delta{t})^2 \end{bmatrix} =E([41a2(Δt)421a2(Δt)321a2(Δt)3a2(Δt)2]=E(a2)[41(Δt)421(Δt)321(Δt)3(Δt)2]
其中 E ( a 2 ) = v E(a^2)=v E(a2)=v,后面的矩阵是一个常数矩阵。
同理 y t y_t yt部分的方程也可以写成矩阵形式并制定好各个参数。
当参数制定好以后再把滤波的目的写出来: P ( x t ∣ y 1 , . . . , y t ) ∝ P ( x t , y 1 , . . . , y t ) P(x_t|y_1,...,y_t)\propto P(x_t,y_1,...,y_t) P(xt∣y1,...,yt)∝P(xt,y1,...,yt)
而 P ( x t , y 1 , . . . , y t ) ∝ P ( y t ∣ x t , y 1 , . . . , y t − 1 ) P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t,y_1,...,y_t)\propto P(y_t|x_t,y_1,...,y_{t-1})P(x_t|y_1,...,y_{t-1}) P(xt,y1,...,yt)∝P(yt∣xt,y1,...,yt−1)P(xt∣y1,...,yt−1)
其中 P ( x t ∣ y 1 , . . . , y t ) P(x_t|y_1,...,y_t) P(xt∣y1,...,yt)叫作update阶段, P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt−1)叫作prediction。
而预测概率又满足下式: P ( x t ∣ y 1 , . . . , y t − 1 ) = ∫ P ( x t , x t − 1 ∣ y 1 , . . . , y t − 1 ) d x t − 1 P(x_t|y_1,...,y_{t-1})=\int P(x_t,x_{t-1}|y_1,...,y_{t-1})dx_{t-1} P(xt∣y1,...,yt−1)=∫P(xt,xt−1∣y1,...,yt−1)dxt−1
而 ∫ P ( x t , x t − 1 ∣ y 1 , . . . , y t − 1 ) d x t − 1 ∝ ∫ P ( x t ∣ x t − 1 , y 1 , . . . , y t − 1 ) P ( x t − 1 ∣ y 1 , . . . , y t − 1 ) d x t − 1 \int P(x_t,x_{t-1}|y_1,...,y_{t-1})dx_{t-1} \propto \int P(x_t|x_{t-1},y_1,...,y_{t-1})P(x_{t-1}|y_1,...,y_{t-1})dx_{t-1} ∫P(xt,xt−1∣y1,...,yt−1)dxt−1∝∫P(xt∣xt−1,y1,...,yt−1)P(xt−1∣y1,...,yt−1)dxt−1
上式中最后一项即为t-1时刻的update。
整个上述公式说明了update是存在递归的,即我们可以从t-1时刻的update求的t时刻的prediction,又从t时刻的prediction求得t时刻的update。
在递归的过程中,高斯噪声也存在一个传播。
因此卡尔曼滤波做了一件什么事呢?卡尔曼滤波做的事的核心就是通过噪声从上一时刻到这一时刻的传播来完成每一时刻的update和prediction,最终直到t时刻的update。