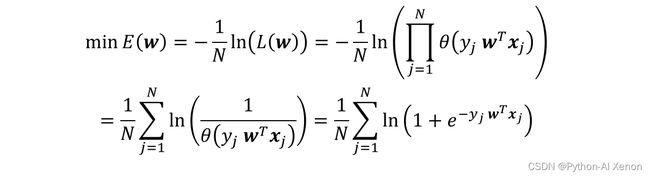Logistic回归实战---疝气病症预测病马的死亡率

Logistic回归实现预测HorseColic

使用Logistic回归来预测患疝气病的马的存活问题(从疝气病症预测病马的死亡率)

一、环境准备

原始数据集下载及说明：http://archive.ics.uci.edu/ml/datasets/Horse+Colic

Python 3.9.13+PyCharm 2022.2.3 (Professional Edition) 或者 jupyter什么的自己选择

sklearn==1.1.3 pip install -U scikit-learn

数据预处理（缺失值问题）

源数据说明: 数据包含368个样本和28个特征.我们使用的时候将其储存如下

• horseColicTraining.txt 作为训练集,包含300个样本
• horseColicTest.txt 作为测试集,包含68个样本

关于28个特征,官网上有详细的介绍，这里我们不用进行深究，从一些文献中了解到，疝病是描述马胃肠痛的术语。然而，这种病不一定源自马的胃肠问题，其他问题也可能引发马疝病。该数据集中包含了医院检测马疝病的一些指标，有的指标比较主观，有的指标难以测量，例如马的疼痛级别。

我们要做的就是通过训练这300个样本，然后对68个样本做测试。

另外需要说明的是，除了部分指标主观和难以测量外，该数据还存在一个问题，数据集中有30%的值是缺失的。

关于缺失值问题，下面给出了一些可选的做法：

• 使用可用特征的均值来填补缺失值；
• 使用特殊值来填补缺失值，如 -1；
• 忽略有缺失值的样本；
• 使用相似样本的均值添补缺失值；
• 使用另外的机器学习算法预测缺失值。

不用担心，我们的数据集只需要做两件事：

第一，所有的缺失值必须用一个实数值0来替换

第二，如果测试集中一条数据的特征值已经缺失，那么我们将该条数据丢弃。

（原因：因为我们如果使用的Numpy数据类型加速计算则不允许包含缺失值。这里选择实数0来替换所有缺失值，恰好能适用于Logistic回归。这样做我们就能得到一个在更新时不会影响系数的值。另外，由于sigmoid(0)=0.5，即它对结果的预测不具由任何倾向性，因此上述做法也不会对误差项造成任何影响。）

原始的数据集经过预处理之后保存成上述两个文件：horseColicTest.txt和horseColicTraining.txt。现在我们就已经初步完成数据的预处理工作了。

预处理完成之后我们还剩下22个可用的特征，已经299条训练数据和67条测试数据。

二、Logistic回归 基础知识

基本公式

深入的大家自行上网查阅相关知识吧,推荐 logistic回归详解 Logistic公式推导 Logistic 回归

• 重点:

logistic回归虽然叫做回归，但却是为了解决分类问题的，是二分类任务的首选方法，简单来说，输出结果不是0就是1

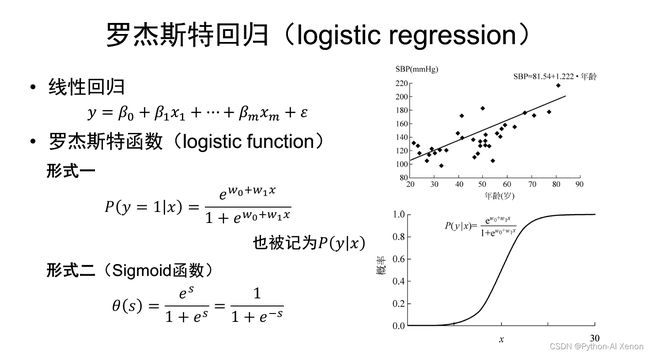
• logistic回归和线性回归的关系

逻辑回归（Logistic Regression）与线性回归（Linear Regression）都是一种广义线性模型（generalized linear model）。
逻辑回归假设因变量 y 服从二项分布，而线性回归假设因变量 y 服从高斯分布。因此与线性回归有很多相同之处，简单认为去除Sigmoid映射函数的话，逻辑回归算法就是一个线性回归。可以说，逻辑回归是以线性回归为理论支持的，但是逻辑回归通过Sigmoid函数引入了非线性因素，因此可以轻松处理0/1分类问题。

• Logistic回归的优缺点

优点：实现简单，易于理解和实现；计算代价不高，速度很快，存储资源低。

缺点：容易欠拟合，分类精度可能不高。

• 适用数据类型：数值型和标称型数据。

最大似然法

梯度下降法

•梯度下降法最优化目标函数 可转化为以下的优化问题：

•算法步骤如下：

三、sk-learn模块基础知识

scikit-learn是一个整合了多种常用的机器学习算法的Python库，又简称skLearn。scikit-learn非常易于使用，为我们学习机器学习提供了一个很好的切入点。

官方英文文档地址 点我查看

码农教程文档 中文文档

class sklearn.linear_model.LogisticRegression 的参数如下所示：

__init__:
penalty: Any = "l2",#惩罚项，str类型，可选参数为l1和l2，默认为l2。
*,
dual: Any = False,	#对偶或原始方法，bool类型，默认为False。
tol: Any = 1e-4,		#停止求解的标准，float类型，默认为1e-4
C: Any = 1.0,			#正则化系数λ的倒数，float类型，默认为1.0
fit_intercept: Any = True,		#是否存在截距或偏差，bool类型，默认为True
intercept_scaling: Any = 1,	#仅在正则化项为”liblinear”，且fit_intercept设置为True时有用。float类型，默认为1。
class_weight: Any = None,	#用于标示分类模型中各种类型的权重，可以是一个字典或者balanced字符串，默认为None
random_state: Any = None,#随机数种子，int类型，可选参数，默认为无，仅在正则化优化算法为sag,liblinear时有用。
solver: Any = "lbfgs",			#优化算法选择参数，只有五个可选参数，即newton-cg,lbfgs,liblinear,sag,saga。默认为liblinear。
max_iter: Any = 100,			#算法收敛最大迭代次数，int类型，默认为100
multi_class: Any = "auto",	#分类方式选择参数，str类型，可选参数为ovr和multinomial，默认为ovr
verbose: Any = 0,				#日志冗长度，int类型。默认为0。
warm_start: Any = False,	#热启动参数，bool类型。默认为False
n_jobs: Any = None,			#并行数。int类型，默认为1
l1_ratio: Any = None) -> None #弹性网混合参数,默认为None

四、Python代码

# -*- coding: utf-8 -*-
# @Author : yxn
# @Date : 2022/11/12 18:49 
# @IDE : PyCharm(2022.2.3) Python3.9.13

# 导入逻辑回归(又名logit, MaxEnt)分类器
from sklearn.linear_model import LogisticRegression


def colicSklearn():
    """处理数据得到训练集、训练集标签、测试集、测试集标签"""
    frTrain = open('horseColicTraining.txt')  # 打开训练集
    frTest = open('horseColicTest.txt')  # 打开测试集
    trainingSet = []  # 创建保存训练数据集的列表
    trainingLabels = []  # 创建保存训练集标签的列表
    testSet = []  # 创建保存测试数据集的列表
    testLabels = []  # 创建保存测试集标签的列表
    # 遍历训练集每个样本
    for line in frTrain.readlines():
        # split__split()通过指定分隔符对字符串进行切片
        # strip__strip()方法用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列
        currLine = line.strip().split('\t')
        lineArr = []  # 创建列表每个样本的特征向量
        for i in range(len(currLine) - 1):  # 遍历训练集每个样本的特征
            lineArr.append(float(currLine[i]))  # 将训练集样本的特征存储在lineArr列表
        trainingSet.append(lineArr)  # 将训练集样本的特征向量存储入数据集列表中
        trainingLabels.append(float(currLine[-1]))  # 将训练集标签列表存储入标签列表

    # 遍历测试集的每个样本
    for line in frTest.readlines():
        currLine = line.strip().split('\t')
        lineArr = []  # 创建特征向量列表
        for i in range(len(currLine) - 1):  # 遍历测试集每个样本的特征
            lineArr.append(float(currLine[i]))  # 将测试集样本的特征存储在lineArr列表
        testSet.append(lineArr)  # 将测试集样本的特征向量存储入数据集列表中
        testLabels.append(float(currLine[-1]))  # 将测试集标签列表存储入标签列表

    return trainingSet, trainingLabels, testSet, testLabels


def run():
    """主函数"""
    # 得到训练集、训练集标签、测试集、测试集标签
    trainingSet, trainingLabels, testSet, testLabels = colicSklearn()
    # 调用sklearn库中的LogisticRegression()完成
    # 参数solver='liblinear'指定优化问题的算法，其内部使用了坐标轴下降法来迭代优化损失函数
    # 参数max_iter=10指定算法收敛最大迭代次数为100，fit根据给定的训练数据拟合模型,返回Fitted estimator.
    classifier = LogisticRegression(solver='liblinear', max_iter=100).fit(trainingSet, trainingLabels)
    # 计算"准确率",score()用于返回给定测试数据和标签的平均精度
    test_accuracy = classifier.score(testSet, testLabels) * 100
    print('训练后对67个样本的正确率为:%f%%' % test_accuracy)


if __name__ == '__main__':
    run()

运行的结果如下：

可以看到我们通过此方法训练的模型对测试集的正确率为73%左右，有待改进。

---

参考链接:

https://www.zhihu.com/column/c_1165018804261785600