自动驾驶算法-滤波器系列（三）——不同运动模型（CV、CA、CTRV、CTRA）的建模和推导

---

上一篇文章主要讲解了不同卡尔曼滤波的原理和特点，其中提到状态预测过程和状态更新两个主要的过程。在将卡尔曼滤波应用在车辆状态跟踪的问题中时，状态预测过程其实就是根据不同的运动模型来对车辆目标的状态进行预测。不同的运动模型是对实际车辆目标的运动过程进行一定的简化来建构的，其中包括一次运动模型和更高级的二次运动模型。本篇文章就是选用不同运动模型来分别构建卡尔曼滤波的模型（包括状态转移矩阵，过程噪声模型的构建和推导，以及不同模型对应的各个矩阵维度的分析）。

0. 运动模型简介

首先要明确的一点是，不管是什么运动模型，本质上都是为了帮助我们简化问题，所以我们可以根据运动模型的复杂程度来进行分类。

一次运动模型（也别称为线性运动模型）：

• 恒定速度模型（Constant Velocity, CV）
• 恒定加速度模型（Constant Acceleration, CA）

二次运动模型：

• 恒定转率和速度模型（Constant Turn Rate and Velocity, CTRV）
• 恒定转率和加速度模型（Constant Turn Rate and Acceleration, CTRA）

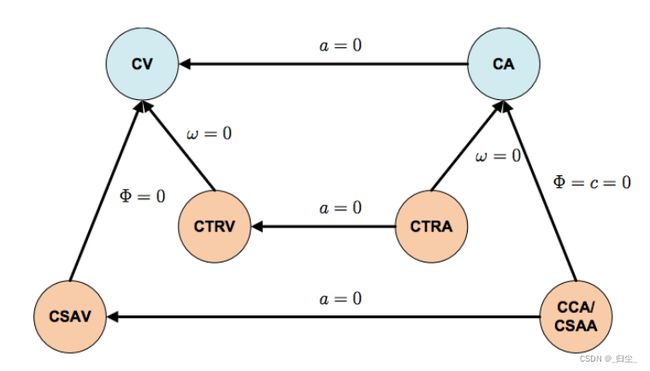
CTRV目前多用于机载追踪系统（飞机），这些二次运动模型大多假定速度$v$和 偏航角速度（yaw rate） $\omega$没有关系，因此，在这类运动模型中，由于偏航角速度测量的扰动（不稳定），即使车辆没有移动，我们的运动模型下的角速度也会发生细微的变化。

为了解决这个问题，速度$v$和 偏航角速度 $\omega$ 的关联可以通过设定转向角$\Phi$恒定来建立，这样就引出了恒定转向角和速度模型（Constant Steering Angle and Velocity，CSAV）； 另外，速度可以别假定为线性变化的，进而引出了常曲率和加速度模型（Constant Curvature and Acceleration，CCA）。

这些运动模型的关系如图：

本篇文章暂时只针对CV, CA, CTRV, CTRA四种运动模型进行建模和推导分析。

1. CV模型

恒定速度模型，（CV，Constant Velocity），模型的速度不变。恒定速度模型的状态空间：
$$x=(x,y,v_x,v_y{)}^T$$
依次为$x$坐标，$y$坐标，$x$速度，$y$速度。

对于$x=(x,y,v_x,v_y{)}^T$，推导运动模型以及状态转移矩阵。
$$\begin{gathered} x_{k+1}=A_k{x}_k+B{u}_k+{\omega }_k \\ {z}_{k+1}=H{x}_{k+1}+{\upsilon }_{k+1} \end{gathered}$$

$A$是状态转移矩阵，$B$是可选的控制输入$u_k$的增益，在大多数实际情况下并没有控制增益，所以$B{u}_k$这一项为零； ${\omega }_k$代表了过程噪声，它对应了每个分量的噪声，是期望为0，协方差矩阵为$Q$的高斯白噪声。

观测方程中, $z_{k+1}$是$m$阶向量，状态变量是$n$阶向量。$H$是$m\ast n$阶矩阵，代表状态变量$x_{k+1}$对测量变量$z_{k+1}$的增益。 观测噪声${\upsilon }_{k+1}$是期望为0，协方差矩阵为$R$的高斯白噪声。

已知上一时刻的状态，推导下一时刻的状态，因为是匀速模型速度不变，故可以根据物理原理$s=s_0+v\Delta t$建模：
$$x_{k+1}={\left\{\begin{array}{c}x\\ y\\ v_x\\ v_y\end{array}\right\}}_{k+1}=\left\{\begin{array}{cccc}1& 0& \Delta t& 0\\ 0& 1& 0& \Delta t\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right\}{\left\{\begin{array}{c}x\\ y\\ v_x\\ v_y\end{array}\right\}}_k$$

上式中的4*4的矩阵即为状态转移矩阵$A$。很显然，车辆不一定会以恒定的速度运动，所以过程包含了一定的过程噪声。在车辆的状态估计中的过程噪声其实就是车的加速度。由分析可知，影响速度的两个参数量，$a_x$和$a_y$。推导出加速度与位移的关系式$s=\frac{1}{2}a{\Delta t}^2$，即可得到过程噪声$\omega$。

$$\omega =\left\{\begin{array}{c}\frac{1}{2}{a}_x{\Delta t}^2\\ \frac{1}{2}{a}_y{\Delta t}^2\\ a_x\Delta t\\ a_y\Delta t\end{array}\right\}=\left\{\begin{array}{cc}\frac{1}{2}{\Delta t}^2& 0\\ 0& \frac{1}{2}{\Delta t}^2\\ \Delta t& 0\\ 0& \Delta t\end{array}\right\}\left\{\begin{array}{c}{a}_x\\ a_y\end{array}\right\}=Gu$$

$$u=\left\{\begin{array}{c}{a}_x\\ a_y\end{array}\right\}G=\left\{\begin{array}{cc}\frac{\Delta t^2}{2}& 0\\ 0& \frac{\Delta t^2}{2}\\ \Delta t& 0\\ 0& \Delta t\end{array}\right\}$$

针对$Q$矩阵，通过最高阶状态量对其他量的扰动来初始化。
关于$Q$矩阵的公式推导：

$$Q=cov(\omega )=E(\omega {\omega }^T)=GE(u{u}^T)G^T=G\left\{\begin{array}{cc}{\sigma }_{a_x}^2& 0\\ 0& {\sigma }_{a_y}^2\end{array}\right\}{G}^T$$

$$Q=\left\{\begin{array}{cccc}0.25{\Delta t}^4{{\sigma }_{a_x}}^2& 0& 0.5{\Delta t}^3{{\sigma }_{a_x}}^2& 0\\ 0& 0.25{\Delta t}^4{{\sigma }_{a_y}}^2& 0& 0.5{\Delta t}^3{{\sigma }_{a_y}}^2\\ 0.5{\Delta t}^3{{\sigma }_{a_x}}^2& 0& {\Delta t}^2{{\sigma }_{a_x}}^2& 0\\ 0& 0.5{\Delta t}^3{{\sigma }_{a_y}}^2& 0& {\Delta t}^2{{\sigma }_{a_y}}^2\end{array}\right\}$$

针对$R$矩阵，根据Gaussian的假设，取各个观测值最大偏差的三倍。尽管这在许多应用中并不合适（比如某些实验不可重复），但有一个准则还是好于任意值。本文中，针对CV模型中$R$矩阵设置如下：
$$R=\left\{\begin{array}{cc}{{\sigma }_x}^2& 0\\ 0& {{\sigma }_y}^2\end{array}\right\}$$

针对观测矩阵$H$，我们结合实际情况，要观测的是位置信息，所以H只需要取状态变量的前两个元素就够了，所以$H$设计成如下形式（注意$H$矩阵的维度 ）：
$$H=\left\{\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right\}$$

针对$P$矩阵，表示协方差矩阵，这个协方差矩阵只要确定了一开始的$P_0$, 后面可以递推出来，而且初始的协方差矩阵只要不是为0，它的取值对滤波效果影响很小，都能很快收敛。
$$P_0=\left\{\begin{array}{cccc}\sum xx& & & \\ & \sum yy& & \\ & & \sum v_x{v}_x& \\ & & & \sum v_y{v}_y\end{array}\right\}$$

总结：

$$A=\left\{\begin{array}{cccc}1& 0& \Delta t& 0\\ 0& 1& 0& \Delta t\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right\}$$

$$B=0$$

$$Q=\left\{\begin{array}{cccc}0.25{\Delta t}^4{{\sigma }_x}^2& 0& 0.5{\Delta t}^3{{\sigma }_x}^2& 0\\ 0& 0.25{\Delta t}^4{{\sigma }_y}^2& 0& 0.5{\Delta t}^3{{\sigma }_y}^2\\ 0.5{\Delta t}^3{{\sigma }_x}^2& 0& {\Delta t}^2{{\sigma }_x}^2& 0\\ 0& 0.5{\Delta t}^3{{\sigma }_y}^2& 0& {\Delta t}^2{{\sigma }_y}^2\end{array}\right\}$$

$$H=\left\{\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right\}$$

$$R=\left\{\begin{array}{cc}{{\sigma }_x}^2& 0\\ 0& {{\sigma }_y}^2\end{array}\right\}$$

$$P=\left\{\begin{array}{cccc}\sum xx& & & \\ & \sum yy& & \\ & & \sum v_x{v}_x& \\ & & & \sum v_y{v}_y\end{array}\right\}$$

已知状态空间的维度是4x1。

矩阵	A	B	Q	H	R	P
维度	4x4（与状态空间维度有关）	4×n（n为输入的列数）	4x4	2x4（2是z的维度，4是x的维度）	2x2（与z的维度有关）	4x4

CV模型的局限性：假设速度是常量，简化了车辆实际移动的形式，相对于匀加速模型来说过于简单。

2. CA模型

恒定加速度模型，（CA，constant acceleration），恒定加速度不变。CA模型有两种状态空间表达：
$$x=(x,y,v_x,v_y,a_x,a_y{)}^T$$
依次为$x$坐标，$y$坐标，$x$速度，$y$速度，$x$加速度，$y$加速度。

对于$x=(x,y,v_x,v_y,a_x,a_y{)}^T$，推导运动模型以及状态转移矩阵。

$$\begin{gathered} x_{k+1}=A_k{x}_k+B{u}_k+{\omega }_k \\ {z}_{k+1}=H{x}_{k+1}+{\upsilon }_{k+1} \end{gathered}$$

已知上一时刻的状态，推导下一时刻的状态，因为是匀加速模型加速度不变，故可以根据物理原理$s=s_0+v\Delta t+\frac{1}{2}a\Delta t^2$建模，得到：
$$x_{k+1}={\left\{\begin{array}{c}x\\ y\\ v_x\\ v_y\\ a_x\\ a_y\end{array}\right\}}_{k+1}=\left\{\begin{array}{cccccc}1& 0& \Delta t& 0& \frac{1}{2}\Delta t^2& 0\\ 0& 1& 0& \Delta t& 0& \frac{1}{2}\Delta t^2\\ 0& 0& 1& 0& \Delta t& 0\\ 0& 0& 0& 1& 0& \Delta t\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right\}{\left\{\begin{array}{c}x\\ y\\ v_x\\ v_y\\ a_x\\ a_y\end{array}\right\}}_k$$

则$A$矩阵为：
$$A=\left\{\begin{array}{cccccc}1& 0& \Delta t& 0& \frac{1}{2}\Delta t^2& 0\\ 0& 1& 0& \Delta t& 0& \frac{1}{2}\Delta t^2\\ 0& 0& 1& 0& \Delta t& 0\\ 0& 0& 0& 1& 0& \Delta t\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right\}$$

在匀加速车辆模型的状态估计中的过程噪声是车的加速度的变化率。由分析可知，影响速度的两个参数量，${\dot{a}}_x$和${\dot{a}}_y$。推导出位移和加速度变化率的关系式，$s=\frac{1}{6}\dot{a}\Delta t^3$，既可以得到过程噪声$\omega$。
$$\omega =\left\{\begin{array}{c}\frac{1}{6}{\dot{a}}_x{\Delta t}^3\\ \frac{1}{6}{\dot{a}}_y{\Delta t}^3\\ \frac{1}{2}{\dot{a}}_x\Delta t^2\\ \frac{1}{2}{\dot{a}}_y\Delta t^2\\ {\dot{a}}_x\Delta t\\ {\dot{a}}_y\Delta t\end{array}\right\}=\left\{\begin{array}{cc}\frac{1}{6}{\Delta t}^3& 0\\ 0& \frac{1}{6}{\Delta t}^3\\ \frac{1}{2}\Delta t^2& 0\\ 0& \frac{1}{2}\Delta t^2\\ \Delta t& 0\\ 0& \Delta t\end{array}\right\}\left\{\begin{array}{c}{\dot{a}}_x\\ {\dot{a}}_y\end{array}\right\}=Gu$$

$$G=\left\{\begin{array}{cc}\frac{1}{6}{\Delta t}^3& 0\\ 0& \frac{1}{6}{\Delta t}^3\\ \frac{1}{2}\Delta t^2& 0\\ 0& \frac{1}{2}\Delta t^2\\ \Delta t& 0\\ 0& \Delta t\end{array}\right\}u=\left\{\begin{array}{c}{\dot{a}}_x\\ {\dot{a}}_y\end{array}\right\}$$

针对$Q$矩阵，通过最高阶状态量对其他量的扰动来初始化。关于$Q$矩阵的公式推导：
$$Q=cov(\omega )=E[(Gu)(Gu{)}^T]=GE[u^2]G^T=G\left\{\begin{array}{cc}{{\sigma }_{{\dot{a}}_x}}^2& 0\\ 0& {{\sigma }_{{\dot{a}}_y}}^2\end{array}\right\}{G}^T$$

$$Q=\left\{\begin{array}{cc}\frac{1}{6}{\Delta t}^3& 0\\ 0& \frac{1}{6}{\Delta t}^3\\ \frac{1}{2}\Delta t^2& 0\\ 0& \frac{1}{2}\Delta t^2\\ \Delta t& 0\\ 0& \Delta t\end{array}\right\}\left\{\begin{array}{cc}{{\sigma }_{{\dot{a}}_x}}^2& 0\\ 0& {{\sigma }_{{\dot{a}}_y}}^2\end{array}\right\}{\left\{\begin{array}{cc}\frac{1}{6}{\Delta t}^3& 0\\ 0& \frac{1}{6}{\Delta t}^3\\ \frac{1}{2}\Delta t^2& 0\\ 0& \frac{1}{2}\Delta t^2\\ \Delta t& 0\\ 0& \Delta t\end{array}\right\}}^T$$

这里的R矩阵设置为：
$$R=\left\{\begin{array}{cc}{{\sigma }_x}^2& 0\\ 0& {{\sigma }_y}^2\end{array}\right\}$$

针对观测矩阵$H$，我们结合实际情况，要观测的是位置信息，所以H只需要取状态变量的前两个元素就够了，所以$H$设计成如下形式（要注意$H$矩阵的维度）：
$$H=\left\{\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\end{array}\right\}$$

P矩阵如下：
$$P=\left\{\begin{array}{cccccc}\sum xx& & & & & \\ & \sum yy& & & & \\ & & \sum v_x{v}_x& & & \\ & & & \sum v_y{v}_y& & \\ & & & & \sum a_x{a}_x& \\ & & & & & \sum a_y{a}_y\end{array}\right\}$$

总结：
$$A=\left\{\begin{array}{cccccc}1& 0& \Delta t& 0& \frac{1}{2}\Delta t^2& 0\\ 0& 1& 0& \Delta t& 0& \frac{1}{2}\Delta t^2\\ 0& 0& 1& 0& \Delta t& 0\\ 0& 0& 0& 1& 0& \Delta t\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right\}$$

$$B=0$$

$$Q=\left\{\begin{array}{cc}\frac{1}{6}{\Delta t}^3& 0\\ 0& \frac{1}{6}{\Delta t}^3\\ \frac{1}{2}\Delta t^2& 0\\ 0& \frac{1}{2}\Delta t^2\\ \Delta t& 0\\ 0& \Delta t\end{array}\right\}\left\{\begin{array}{cc}{{\sigma }_{{\dot{a}}_x}}^2& 0\\ 0& {{\sigma }_{{\dot{a}}_y}}^2\end{array}\right\}{\left\{\begin{array}{cc}\frac{1}{6}{\Delta t}^3& 0\\ 0& \frac{1}{6}{\Delta t}^3\\ \frac{1}{2}\Delta t^2& 0\\ 0& \frac{1}{2}\Delta t^2\\ \Delta t& 0\\ 0& \Delta t\end{array}\right\}}^T$$

$$R=\left\{\begin{array}{cc}{{\sigma }_x}^2& 0\\ 0& {{\sigma }_y}^2\end{array}\right\}$$

$$H=\left\{\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\end{array}\right\}$$

$$P=\left\{\begin{array}{cccccc}\sum xx& & & & & \\ & \sum yy& & & & \\ & & \sum v_x{v}_x& & & \\ & & & \sum v_y{v}_y& & \\ & & & & \sum a_x{a}_x& \\ & & & & & \sum a_y{a}_y\end{array}\right\}$$

已知状态空间的维度是6x1。

矩阵	A	B	Q	H	R	P
维度	6x6（与状态空间维度有关）	6×n（n为输入的列数）	6x6	2x6（2是z的维度，4是x的维度）	2x2（与z的维度有关）	6x6

CA模型：相比于CV模型来说，速度由匀速变成了匀加速，但是由于大多数车辆道路是有拐弯的，CA模型会无法正确预测拐弯车辆。

3. CTRV模型

恒定转弯率和速度模型，（CTRV，Constant Turn Rate and Velocity），此模型假设对象沿直线前进，同时还能以固定的转弯速率和恒定的速度大小移动。

状态空间如下：
$$x=(x,y,v,\psi ,\dot{\psi }{)}^T$$

上式中变量依次为：$x$坐标，$y$坐标，$v$速度，$\psi$偏航角（与$x$夹角逆时针为正），$\dot{\psi }$角速度。

由运动方程分析可以得到系统的差分方程：

$$\begin{array}{c}\dot{x}=v_x=v\cos (\psi )\\ \dot{y}=v_y=v\sin (\psi )\\ \dot{v}=0\\ \dot{\psi }=\dot{\psi }\\ \ddot{\psi }=0\end{array}\Rightarrow \left\{\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{v}\\ \dot{\psi }\\ \ddot{\psi }\end{array}\right\}=\left\{\begin{array}{c}v\cos (\psi )\\ v\sin (\psi )\\ 0\\ \dot{\psi }\\ 0\end{array}\right\}$$

假设离散的时间步骤$k$和持续的时间值$t_k$相关，离散的时间步骤$k+1$和持续的时间值$t_{k+1}$相关，$t_{k+1}$和$t_k$之间的时间差叫做$\Delta t$。

当${\dot{\psi }}_k\ne 0$时，
$$x_{k+1}=x_k+\left\{\begin{array}{c}{\int }_{t_k}^{t_{k+1}}v(t)\cos (\psi (t))dt\\ {\int }_{t_k}^{t_{k+1}}v(t)\sin (\psi (t))dt\\ 0\\ {\dot{\psi }}_k\Delta t\\ 0\end{array}\right\}$$

将$\psi (t)={\psi }_k+{\dot{\psi }}_k(t-t_k)$带入上式中，同时计算积分，得到：
$$x_{k+1}=x_k+\left\{\begin{array}{c}\frac{v_k}{{\dot{\psi }}_k}(\sin ({\psi }_k+{\dot{\psi }}_k\Delta t)-\sin ({\psi }_k))\\ \frac{v_k}{{\dot{\psi }}_k}(-\cos ({\psi }_k+{\dot{\psi }}_k\Delta t)+\cos ({\psi }_k))\\ 0\\ {\dot{\psi }}_k\Delta t\\ 0\end{array}\right\}$$

当${\dot{\psi }}_k=0$时，实际上是直线行驶，
$$\begin{gathered} x=v_k\cos ({\psi }_k)\Delta t \\ y=v_k\sin ({\psi }_k)\Delta t \end{gathered}$$

CTRV模型中，假定车的纵向速度和角速度为恒定值，忽略了速度变化，因此把加速度项的影响放到了误差里面。

噪声分为两个部分，加速度${\upsilon }_{a,k}$和${\upsilon }_{\ddot{\psi },k}$，

$${\upsilon }_k=\left\{\begin{array}{c}{\upsilon }_{a,k}\\ {\upsilon }_{\ddot{\psi },k}\end{array}\right\}$$

其中：
${\upsilon }_{a,k}\sim N(0,{\sigma }_a^2)$纵向加速度噪声，表示在纵向速度上的不确定性；
${\upsilon }_{\ddot{\psi },k}\sim N(0,{\sigma }_{\stackrel{..}{\psi }}^2)$角加速度噪声，表示偏航角上的不确定性。

假设误差项，偏航角角加速度和纵向加速度是常量，那么在时间差内产生的误差$a,b,c,d,e$可定义为：

$$\begin{gathered} a=\frac{1}{2}{\upsilon }_{a,k}\cos ({\psi }_k)\Delta t^2 \\ b=\frac{1}{2}{\upsilon }_{a,k}\sin ({\psi }_k)\Delta t^2 \\ c=\Delta t{\upsilon }_{a,k} \\ d=\frac{1}{2}{\upsilon }_{\ddot{\psi },k}\Delta t^2 \\ e=\Delta t{\upsilon }_{\ddot{\psi },k} \end{gathered}$$

则完整的状态方程为：
$$\left\{\begin{array}{c}{x}_{k+1}\\ y_{k+1}\\ v_{k+1}\\ {\psi }_{k+1}\\ {\dot{\psi }}_{k+1}\end{array}\right\}=\left\{\begin{array}{c}{x}_k+\frac{v_k}{\dot{{\psi }_k}}(\sin ({\psi }_k+\dot{{\psi }_k}\Delta t)-\sin ({\psi }_k))\\ y_k+\frac{v_k}{\dot{{\psi }_k}}(-\cos ({\psi }_k+\dot{{\psi }_k}\Delta t)+\cos ({\psi }_k))\\ v_k\\ {\psi }_k+\dot{{\psi }_k}\Delta t\\ \dot{{\psi }_k}\end{array}\right\}+\left\{\begin{array}{c}\frac{1}{2}{\upsilon }_{a,k}\cos ({\psi }_k)\Delta t^2\\ \frac{1}{2}{\upsilon }_{a,k}\sin ({\psi }_k)\Delta t^2\\ \Delta t{\upsilon }_{a,k}\\ \frac{1}{2}{\upsilon }_{\ddot{\psi },k}\Delta t^2\\ \Delta t{\upsilon }_{\ddot{\psi },k}\end{array}\right\},\dot{{\psi }_k}\ne 0$$

$$\left\{\begin{array}{c}{x}_{k+1}\\ y_{k+1}\\ v_{k+1}\\ {\psi }_{k+1}\\ {\dot{\psi }}_{k+1}\end{array}\right\}=\left\{\begin{array}{c}{x}_k+v_k\cos ({\psi }_k)\Delta t\\ y_k+v_k\sin ({\psi }_k)\Delta t\\ v_k\\ {\psi }_k+\dot{{\psi }_k}\Delta t\\ \dot{{\psi }_k}\end{array}\right\}+\left\{\begin{array}{c}\frac{1}{2}{\upsilon }_{a,k}\cos ({\psi }_k)\Delta t^2\\ \frac{1}{2}{\upsilon }_{a,k}\sin ({\psi }_k)\Delta t^2\\ \Delta t{\upsilon }_{a,k}\\ \frac{1}{2}{\upsilon }_{\ddot{\psi },k}\Delta t^2\\ \Delta t{\upsilon }_{\ddot{\psi },k}\end{array}\right\},\dot{{\psi }_k}=0$$

可知CTRV模型是非线性的，需要线性化处理才能应用卡尔曼滤波。

过程噪声$\upsilon$
$$\upsilon =\left\{\begin{array}{c}\frac{1}{2}{a}_k\cos ({\psi }_k)\Delta t^2\\ \frac{1}{2}{a}_k\sin ({\psi }_k)\Delta t^2\\ \Delta t{a}_k\\ \frac{1}{2}{\ddot{\psi }}_k\Delta t^2\\ \Delta t\ddot{{\psi }_k}\end{array}\right\}=\left\{\begin{array}{cc}\frac{1}{2}\cos ({\psi }_k)\Delta t^2& 0\\ \frac{1}{2}\sin ({\psi }_k)\Delta t^2& 0\\ \Delta t& 0\\ 0& \frac{1}{2}\Delta t^2\\ 0& \Delta t\end{array}\right\}\left\{\begin{array}{c}{a}_k\\ \ddot{{\psi }_k}\end{array}\right\}=Gu$$

针对$Q$矩阵，

$$Q=cov(\upsilon )=E[(Gu)(Gu{)}^T]=GE[u^2]G^T=G\left\{\begin{array}{cc}{{\sigma }_{a_k}}^2& 0\\ 0& {{\sigma }_{{\ddot{\psi }}_k}}^2\end{array}\right\}{G}^T$$

$$Q=\left\{\begin{array}{cc}\frac{1}{2}\cos ({\psi }_k)\Delta t^2& 0\\ \frac{1}{2}\sin ({\psi }_k)\Delta t^2& 0\\ \Delta t& 0\\ 0& \frac{1}{2}\Delta t^2\\ 0& \Delta t\end{array}\right\}\left\{\begin{array}{cc}{{\sigma }_{a_k}}^2& 0\\ 0& {{\sigma }_{{\ddot{\psi }}_k}}^2\end{array}\right\}{\left\{\begin{array}{cc}\frac{1}{2}\cos ({\psi }_k)\Delta t^2& 0\\ \frac{1}{2}\sin ({\psi }_k)\Delta t^2& 0\\ \Delta t& 0\\ 0& \frac{1}{2}\Delta t^2\\ 0& \Delta t\end{array}\right\}}^T$$

针对$H$矩阵，需要观测的量为$x，y$的坐标和偏航角，故$H$是3x5维的矩阵。
$$H=\left\{\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 0\end{array}\right\}$$

针对$P$矩阵，在CTRV模型中，状态的数量$n$除了要包含5个状态以外，还要包括处理噪声，因为这些处理噪声对模型也有着非线性的影响。在增加了处理噪声的影响以后，我们的不确定性矩阵P就变成了：
$$P=\left\{\begin{array}{cc}P\prime & 0\\ 0& Q\end{array}\right\}$$

4. CTRA模型

恒定转弯率和加速度模型。（CTRA，Constant Turn Rate and Acceleration）。同CTRV相比，转速不变，说明在相同时间内转过的角度是一样的，径向速度由匀速变成了匀加速，那么对应的位移会变长。

状态空间：
$$x=(x,y,\psi ,v,a,\omega {)}^T$$

在状态空间中，车辆的加速度和角速度是不会发生变化的。

系统的差分方程：
$$\begin{gathered} \stackrel{.}{x}=v_x=(v_k+a\Delta t)\cos ({\psi }_k+\omega \Delta t) \\ \stackrel{.}{y}=v_y=(v_k+a\Delta t)\sin ({\psi }_k+\omega \Delta t) \\ \stackrel{.}{\psi }=\omega \\ \stackrel{.}{v}=a \\ \stackrel{.}{a}=0 \\ \stackrel{.}{\omega }=0 \end{gathered}$$

对差分方程，我们在$t_k$和$t_{k+1}$上积分，得到$\Delta t(\Delta t=t_{k+1}-t_k)$时间 段内的增量。运动方程如下：
x k + 1 = x k + { g x ( x k , Δ t ) g y ( x k , Δ t ) ω Δ t a Δ t 0 0 } x_{k+1}=x_k+ \left\{\begin{matrix} g_x(x_k,\Delta t)\\ g_y(x_k,\Delta t)\\ \omega \Delta t\\ a\Delta t\\ 0\\ 0 \end{matrix}\right\} xk+1​=x