自动驾驶路径规划——人工势场法
目录
- 前言
- 1. 人工势场法
-
- 1.1 引力势场函数模型
-
- 1.1.1 MATLAB中实现引力函数模型
- 1.2 斥力势场函数模型
-
- 1.2.1 MATLAB中实现斥力函数
- 1.3 合势场模型
- 2. 人工势场法实现流程
- 3. 人工势场法的优缺点
- 4. 人工势场法改进算法
-
- 4.1障碍物斥力场改进
- 4.2 局部极小值改进
-
- 4.2.1 引入虚拟力
- 4.2.2 障碍物连锁网络结构
- 4.2.3 选取子目标点
- 4.3 动态避障能力提升改进
-
- 4.3.1 建立速度斥力场函数
- 声明
前言
这个学期学校开设了相应的课程,同时也在学习古月居机器人学系列的《基于栅格地图的机器人路径规划指南》,为了巩固知识,方便自己的学习与整理,遂以学习笔记的形式记录。
1. 人工势场法
人工势场法(artificial potential field,APF)是由Oussama Khatib博士提出的一种应用于研究机器人的路径方法。人工势场法的基本原理就是通过一系列环境感知传感器来探知环境的障碍物情况,无人车在多个斥力势场和一个引力势场的和势场环境下沿着势场下降的方向运动。人工势场法是一种广泛应用的路径规划方法,适用于已知环境或未知环境。人工势场法本质上是一种控制方法,其轨迹并非像其他规划算法一样,而是由实时的控制量产生的。
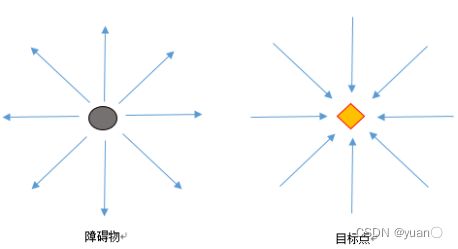
APF算法是一种假设的虚拟势力场法,其相关的设定类似于磁场,同性相斥,异性相吸,其中,
目标点对无人车辆产生的引力势场 方向是从无人车到目标位置;
障碍物对无人车辆产生的斥力势场 方向是从障碍物到无人车位置。

在势场中,无人车会受到来自所有势场叠加的力,作用力的规则满足平行四边形法则,合力将会驱动无人车向目标点运动。无人车辆在这两种势力场合的作用下,沿着合势力场梯度下降最快的方向朝目标点移动。我们为了便于理解可以把引力势场看作是一个山谷区,把障碍物产生的斥力势场看作是一个高峰区,无人驾驶汽车就像水流一样,从地势较高地区向地势较低地区运动,最后到达地势最低的位置即为目标点。
1.1 引力势场函数模型
在势场中目标位置对无人车产生吸引的影响,构成引力势场,驱动着无人驾驶汽车向着希望的目标位置运动。无人驾驶汽车所受的引力大小主要和汽车与目标位置的间隔距离有关系,若无人车与目标位置间隔越大,引力就越大;反之,引力就越小。当无人汽车到达目标位置的时候,车和目标位置的间距为零,因此,无人车所受的引力逐渐减小为零。通过查阅资料发现,无人车引力和无人车、目标点三者之间的距离是成正比关系,因此,我们可以使用幂函数来对定义引力势场:
U a t t = 1 2 K a t t P 0 m U_{att} = \frac{1}{2}K_{att}P_0^m Uatt=21KattP0m
式中 Katt —— 引力势场正比列系数;
P0 —— 无人驾驶车辆和目标点位置的直线距离;
m —— 引力势场因子。
通常我们取引力势场因子m=2,引力势场正比列系数Katt可以任意选取,我选取20。
无人驾驶汽车受到引力Fatt作用,引力Fatt是引力势场函数Uatt的负导数,意义是引力势场的变化最快方向。引力的大小是引力势场函数对无人车和目标位置之间的距离取的导数,因此可得:
F a t t ( P 0 ) = − ∇ U a t t ( P 0 ) = − K a t t P 0 F_{att}(P0) = - \nabla U_{att}(P0) = - K_{att}P0 Fatt(P0)=−∇Uatt(P0)=−KattP0
引力函数采用的模型类似于弹力模型,距离越远,引力越大,相应的无人车的速度就会越大。
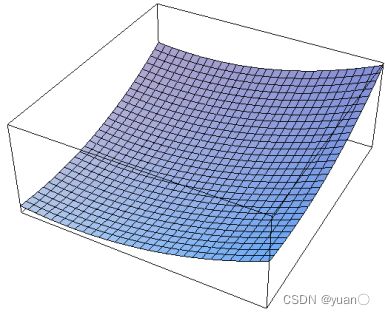
引力势场函数值受无人车辆和目标点之间的距离影响,距离越大,引力势场值越大,距离越小,引力势场值越小。
1.1.1 MATLAB中实现引力函数模型
function [Fattx,Fatty]=compute_Attract(currentPoint,finalPoint,Katt,angleGoal)
%输入参数为当前坐标,目标坐标,引力增益常数,力的角度
r=norm(currentPoint-finalPoint);%路径点和目标的距离,欧式几何距离
Fattx=Katt*r*cos(angleGoal);%angle=Y(1)
Fatty=Katt*r*sin(angleGoal);
end
% Uatt=1/2.0*Katt*r*r;
1.2 斥力势场函数模型
在人工势场法中障碍物对智能驾驶汽车会产生排斥的影响,构成斥力势场,引导着无人驾驶汽车远离障碍物运动,从而顺利躲避障碍物顺利到达目标点。无人驾驶汽车所受的斥力大小和距离有关系,此距离大小就是车和障碍物相隔的距离,如果无人车和障碍物相隔的距离很小,斥力就很大;反之,斥力就很小。当无人汽车离开障碍物时,如果两者之间的距离超过斥力势场的影响范围,无人车不会受到斥力的影响。斥力函数如下:
U r e p ( P g ) = { 1 2 K r e p ( 1 P g − 1 ρ ) 2 , P g ≤ ρ 0 , P g > ρ Urep(Pg) = \left\{ {\begin{array}{ccccccccccccccc}{\frac{{\rm{1}}}{{\rm{2}}}Krep{{\left( {\frac{1}{{Pg}} - \frac{1}{\rho }} \right)}^2},Pg \le \rho }\\{0,{\rm{ }}Pg > \rho }\end{array}} \right. Urep(Pg)={21Krep(Pg1−ρ1)2,Pg≤ρ0,Pg>ρ
F r e p ( P g ) = { K r e p ( 1 P g − 1 ρ ) 1 P g 2 , P g ≤ ρ 0 , P g > ρ Frep(Pg) = \left\{ {\begin{array}{ccccccccccccccc}{Krep(\frac{1}{{Pg}} - \frac{1}{\rho })\frac{1}{{P_g^2}},Pg \le \rho }\\{0,{\rm{ }}Pg > \rho }\end{array}} \right. Frep(Pg)={Krep(Pg1−ρ1)Pg21,Pg≤ρ0,Pg>ρ
式中 ρ —— 障碍物对无人车产生斥力的最大作用范围;
Pg —— 障碍物和无人车的距离;
Krep —— 斥力势场中的正比例系数。
当无人车辆进入障碍物的影响范围时,两者之间距离越大,斥力势场值应越小;反之,距离越小,势场值应越大。同样的,由于无人车需要控制指令去操控,所以当距离越小时,其转向角也会增大,有快速偏离障碍物之效。

1.2.1 MATLAB中实现斥力函数
function [Frepx,Frepy]=compute_repulsion(currentPoint,obstaclePoint,Krep,angle,obstacleNum,influenceDistance,finalPoint)
%输入参数为当前坐标,Xsum是目标和障碍的坐标向量,增益常数,障碍,目标方向的角度
r=norm(currentPoint-finalPoint);
for i=1:obstacleNum
currentObstacle=norm(currentPoint-obstaclePoint(i,:));%路径点和障碍的距离保存在数组rrei中
if currentObstacle>influenceDistance%如果每个障碍和路径的距离大于障碍影响距离,斥力令为0
Yrepx(i)=0;
Yrepy(i)=0;
else
Y1=-Krep*(1/currentObstacle-1/influenceDistance)*(1/(currentObstacle*currentObstacle));%分解的Fre1向量
Yrepx(i)=Y1*cos(angle(i+1));%障碍物的点从初始化点中第二个记起
Yrepy(i)=Y1*sin(angle(i+1));
end
end
Frepx=sum(Yrepx);%叠加斥力的分量
Frepy=sum(Yrepy);
end
1.3 合势场模型
根据人工势场法的基础原理,无人驾驶汽车在这两种势场的环境下运动时,无人车所受的人工势场中的势能是由多个势能矢量相加决定的,因此,无人车所受的力等效于多个斥力与一个目标点的引力的合力。合势场为:
U t a l ( P ) = U a t t ( P ) + U r e p ( P ) Utal(P) = Uatt(P) + Urep(P) Utal(P)=Uatt(P)+Urep(P)
因此,由合势场可知合力的表达式为:
F t a l ( P ) = F a t t ( P ) + F r e p ( P ) Ftal(P) = Fatt(P) + Frep(P) Ftal(P)=Fatt(P)+Frep(P)
直观来讲,可以将引力势场比作凹谷,目标点为凹谷的最低点;将斥力场比作凸峰。车辆的路径规划类似于水往低处流,避开高势能的地方流向低势能的地方。

2. 人工势场法实现流程
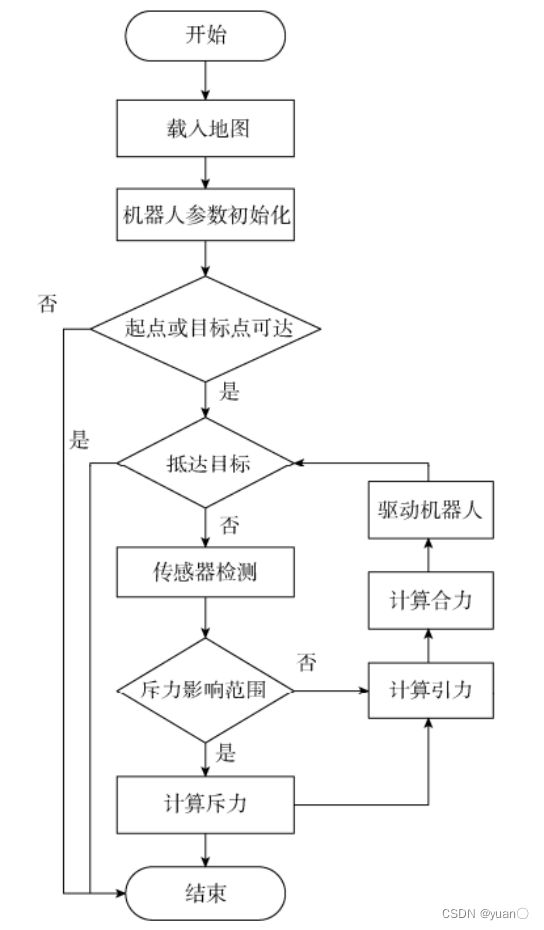
首先载入地图,预设好相关参数,如障碍物的坐标位置、大小等;再对无人车的参数初始化。之后按照上述流程进行。流程图之中有几部分值得注意:
- 如何确定斥力的影响范围对实车效果具有重要作用。理想情况下,我们会设置障碍物的中心坐标作为相应的点,然后适当膨胀,作为斥力的影响范围。实际情况中,我们可能无法得到障碍物具体的中心坐标,且我们通常得到的数据是障碍物的边缘信息,所以通常会选取这些边缘点中离无人车最近的一个点作为影响点来计算距离。
- 在计算斥力上,我们所得到的斥力其实是一个矢量,通常将其分解计算。
- 在计算合力到驱动机器人之间,通过计算出来的合力,发布指令给机器人的底层驱动,控制机器人的转向等运动。
3. 人工势场法的优缺点
优点:
便于低层的实时控制,在实时避障和平滑的轨迹控制方面,得到了广泛应用
缺点:
1.当物体离目标点比较远时,引力将变的特别大,相对较小的斥力在可以忽略的情况下,物体路径上可能会碰到障碍物
2. 当目标点附近有障碍物时,斥力将非常大,引力相对较小,物体很难到达目标点。当小车与目标点距离很近时,若目标点附近有障碍物,此时小车所受引力相对于极大的斥力近似为0,小车将一直在目标点附近徘徊而无法到达目标点。
3. 在某个点,引力和斥力刚好大小相等,方向想反,则物体容易陷入局部最优解或震荡,发生“死锁”现象。如果无人车与障碍物、目标点共线,当无人车进入障碍物影响范围内时,其受到斥力逐渐增大,而引力逐渐减小。因此在障碍物前方某点,会出现合力为0的情况。无人车往复震荡,无法避开障碍物。
4. 动态避障能力差。由公式看出,经典人工势场法只考虑无人车与目标点、障碍物间的距离,因此经典APF常用于静态路径规划。对于动态障碍物或目标点,经典APF法会因为实时性较差而无法得到平滑路径。

5.不适合用作全局路径规划。 经典APF的行驶环境是假定在无限大的区域内,而实际道路是有限范围,所以实用性较差。
人工势场法更适合作为局部避障算法,即在全局路径规划得到行驶路径后,由APF算法控制车辆实现路径跟踪并且避免与新障碍物发生碰撞。
4. 人工势场法改进算法
4.1障碍物斥力场改进
在经典APF的障碍物斥力场模型中,将无人车与目标点间距离考虑进来,使无人车在靠近目标点过程中,斥力也逐渐减小至零。
{ 1 2 γ ( 1 ρ ( X , X o b s ) − 1 ρ 0 ) 2 ( X − X g o a l ) n , ρ ( X , X o b s ) ≤ ρ 0 0 , ρ ( X , X o b s ) > ρ 0 \left\{ {\begin{array}{ccccccccccccccc}{\frac{1}{2}\gamma {{\left( {\frac{1}{{\rho \left( {X,{X_{obs}}} \right)}} - \frac{1}{{{\rho _0}}}} \right)}^2}{{\left( {X - {X_{{\rm{goal}}}}} \right)}^n}}&{,\rho \left( {X,{X_{obs}}} \right) \le {\rho _0}}\\0&{,\rho \left( {X,{X_{obs}}} \right) > {\rho _0}}\end{array}} \right. {21γ(ρ(X,Xobs)1−ρ01)2(X−Xgoal)n0,ρ(X,Xobs)≤ρ0,ρ(X,Xobs)>ρ0 F r e p 1 = { γ ( 1 ρ ( X , X o b s ) − 1 ρ 0 ) ( X − X g o a l ) n ρ ( X , X o b s ) 2 ∇ ρ , ρ ( X , X o b s ) ≤ ρ 0 0 , ρ ( X , X o b s ) > ρ 0 {F_{rep1}} = \left\{ {\begin{array}{ccccccccccccccc}{\gamma \left( {\frac{1}{{\rho \left( {X,{X_{obs}}} \right)}} - \frac{1}{{{\rho _0}}}} \right)\frac{{{{\left( {X - {X_{{\rm{goal}}}}} \right)}^n}}}{{\rho {{\left( {X,{X_{obs}}} \right)}^2}}}\nabla \rho }&{,\rho \left( {X,{X_{obs}}} \right) \le {\rho _0}}\\0&{,\rho \left( {X,{X_{obs}}} \right) > {\rho _0}}\end{array}} \right. Frep1={γ(ρ(X,Xobs)1−ρ01)ρ(X,Xobs)2(X−Xgoal)n∇ρ0,ρ(X,Xobs)≤ρ0,ρ(X,Xobs)>ρ0 F r e p 2 = { n 2 γ ( 1 ρ ( X , X o b s ) − 1 ρ 0 ) ( X − X g o a l ) n − 1 , ρ ( X , X o b s ) ≤ ρ 0 0 , ρ ( X , X o b s ) > ρ 0 {F_{rep2}} = \left\{ {\begin{array}{ccccccccccccccc}{\frac{n}{2}\gamma \left( {\frac{1}{{\rho \left( {X,{X_{obs}}} \right)}} - \frac{1}{{{\rho _0}}}} \right){{\left( {X - {X_{{\rm{goal}}}}} \right)}^{n - 1}}}&{,\rho \left( {X,{X_{obs}}} \right) \le {\rho _0}}\\0&{,\rho \left( {X,{X_{obs}}} \right) > {\rho _0}}\end{array}} \right. Frep2={2nγ(ρ(X,Xobs)1−ρ01)(X−Xgoal)n−10,ρ(X,Xobs)≤ρ0,ρ(X,Xobs)>ρ0

F r e p = F r e p 1 + F r e p 2 {F_{rep}} = {F_{rep1}} + {F_{rep2}} Frep=Frep1+Frep2
Frep1方向为障碍物指向无人车
Frep2方向为无人车指向目标点
4.2 局部极小值改进
4.2.1 引入虚拟力
当陷入局部极小值时,可以用虚拟力进行逃离。也可以采用随机的方法,跳出局部极小值的状态。
4.2.2 障碍物连锁网络结构
当多个障碍物呈U型分布时,无人车容易陷入局部极小值。将近距离密集分布的多个障碍物连锁起来,形成一个大障碍物,进行大范围区域避障。

具体步骤:
- 确定搜索范围D,搜索障碍物1周围是否存在其他障碍物。如果有,则与障碍物1距离最小的障碍物建立连锁。如左图中障碍物1与2建立连锁。
- 做OA和OB的延长线形成阴影区域。如果该区域有障碍物,是为被遮挡,不进行连锁。显然3被遮挡,4没被遮挡。算法中,若向量OA×OB与CA×CB异号,向量AO×AC与BO×BC异号,则可判断障碍物3被遮挡。
- 选择其它未被连锁或遮挡的障碍物,重复上述步骤。

4.2.3 选取子目标点
通过合理选取横向子目标点M和纵向子目标点O
打破力的平衡,即可使小车逃出局部极小值

建立子目标点引力势场来避免局部最优解导致的避障失败。当无人车在障碍物的影响范围时,选择纵向和横向子目标点。然后根据选定的子目标点建立引力场。横向子目标点引力场使无人车转向障碍物一侧,以避免引力和斥力共线造成的局部最优解。纵向子目标点引力场使无人车以平滑轨迹避障并返回全局路径。
子目标点的选择可分为以下三种情况,如下图所示。
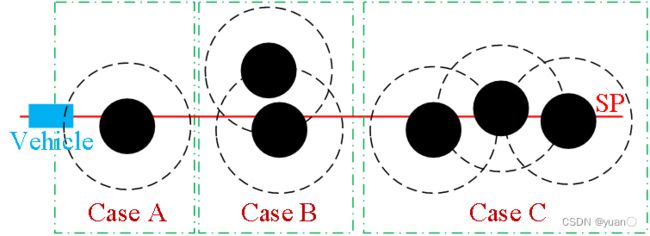
首先确定从每一侧避开障碍物的横向偏差,选取横向偏差小的那一边。当有多个不同大小的障碍物时,选取影响范围更大的障碍物作为子目标点。

4.3 动态避障能力提升改进
4.3.1 建立速度斥力场函数
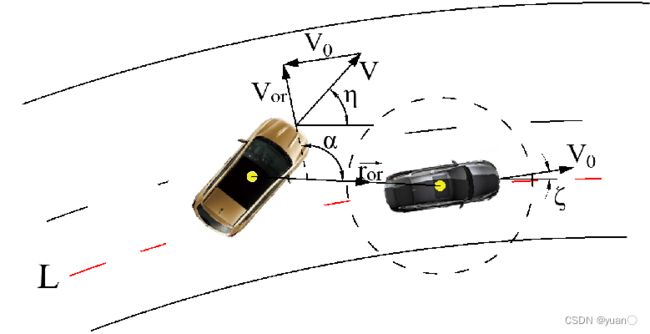
U r e p v = { 1 2 k v v o r 2 0 ≤ ρ ≤ ρ 0 ∩ α ∈ ( − π 2 , π 2 ) 0 e l s e {U_{repv}} = \left\{ {\begin{array}{ccccccccccccccc}{\frac{1}{2}{k_v}v_{or}^2}&{0 \le \rho \le {\rho _0} \cap \alpha \in \left( { - \frac{\pi }{2},\frac{\pi }{2}} \right)}\\0&{else}\end{array}} \right. Urepv={21kvvor200≤ρ≤ρ0∩α∈(−2π,2π)else
F r e p v = { k v v o r 0 ≤ ρ ≤ ρ 0 ∩ α ∈ ( − π 2 , π 2 ) 0 e l s e {F_{repv}} = \left\{ {\begin{array}{ccccccccccccccc}{{k_v}v_{or}^{}}&{0 \le \rho \le {\rho _0} \cap \alpha \in \left( { - \frac{\pi }{2},\frac{\pi }{2}} \right)}\\0&{else}\end{array}} \right. Frepv={kvvor00≤ρ≤ρ0∩α∈(−2π,2π)else
声明
本人所有文章仅作为自己的学习记录,若有侵权,联系立删。