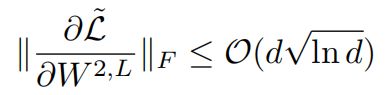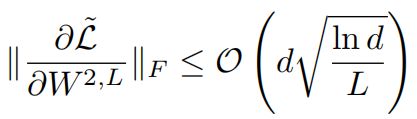BERT模型—1.BERT模型架构
文章目录
-
-
- 引言
- 一、Bert模型总览
- 二、注意力机制
-
- 1.Seq2seq中的注意力操作
- 2.注意力的一般形式（三步曲）
- 3. transformer中的自注意力机制—Self.Attention
- 4. transformer的多头注意力机制
- 5. scaling
- 6. 模型优化技巧：残差连接
- 三、BERT其他结构特性
-
- 1.BERT模型中的位置编码
- 2. BERT中的全连接层与非线性激活函数
- 3. 层归一化—LayerNormalization
-
引言
本节将按照思维导图逐步了解BERT模型。
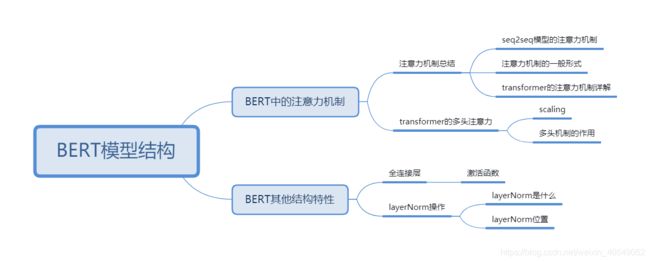
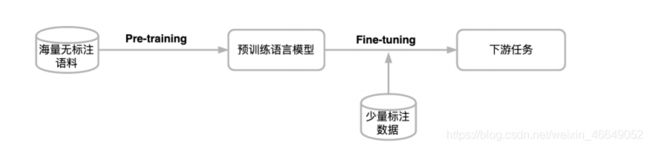
2018年谷歌在Github上开源了Bert模型之后，后续人们开发Bert模型变体以及对Bert模型进行优化，各种NLP比赛榜单都是Bert及其变体占据，开启了NLP的新时代！这个时代有两个特性：
- 模型的架构是趋同的，所有的模型基本上是基于transformer的
- 所有的模型基本上都是基于预训练的
一、Bert模型总览
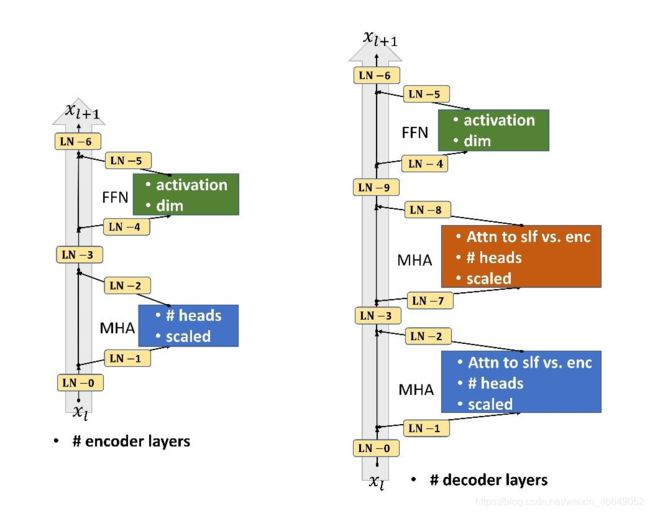
BERT网络结构是多层transformer Encoder叠加。
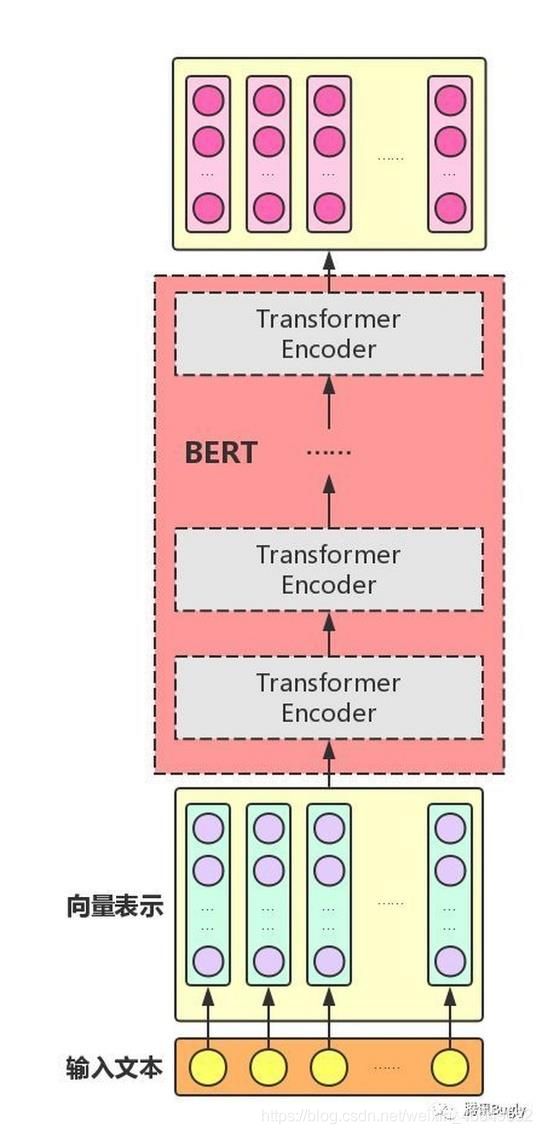
Transformer block的具体架构为：
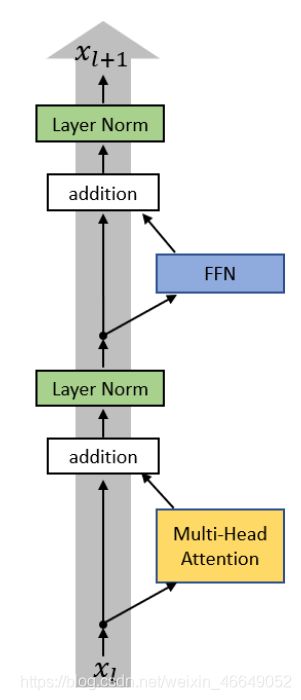
Transformer层的网络核心要素如下:
- Multi-head attention (多头注意力)
- FFN(全连接层)
- LayerNorm(层归一化)
- 残差连接
二、注意力机制
人类在接收到所有信号时，并不会将注意力平分到每一个信号中，而是会重点观察某些部分，战略性忽略某些部分。
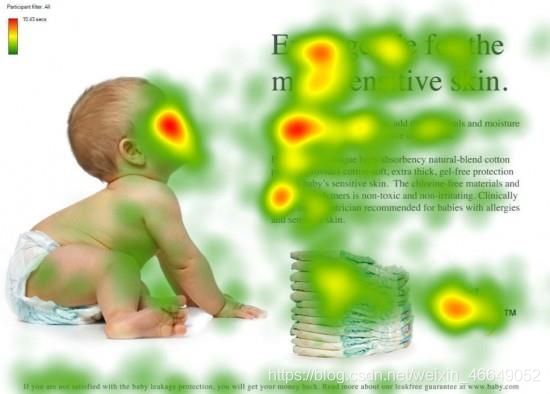
NLP中核心的注意力机制与人类的注意力机制在直观上是一致的。
1.Seq2seq中的注意力操作
我们现在从attention的起源来了解attention的功能。在没有attention机制以前，机器翻译模型通常是使用序列到序列的架构（Seq2seq）。
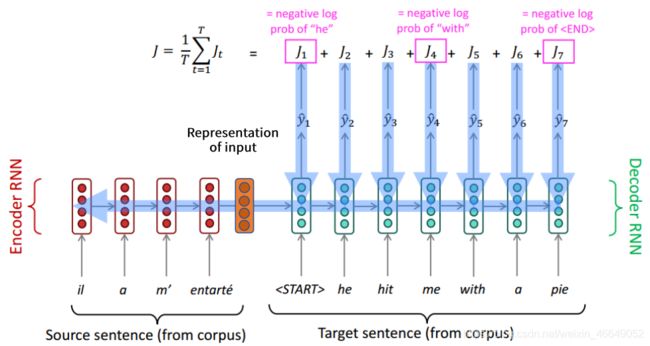
左边的编码器（Encoder）将原文直接表示成向量，这个向量用于目标语言句子的预测中，在解码器（Decoder）生成目标语言句子。这个模型架构逻辑上是非常合理的，但是会涉及到信息瓶颈的问题—即输入的句子不管有多丰富，但是面对解码器，最终只会生成一个向量。在预测目标语言句子的不同字时，所拥有的输入信息（原句输入信息）是相同的（输入句子全部局限于向量表示中）。不过，我们在预测目标语言句子的不同字时，需要关注输入的不同部分。
例如：翻译句子的前面几个字，大概率是基于句子靠前部分来翻译；翻译句子的后面几个字，大概率是基于句子靠后部分来翻译的。
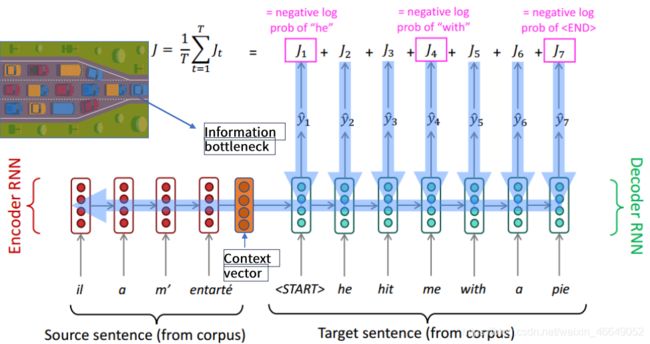
为了解决“信息瓶颈”的问题，引入了attention机制，打开了NLP架构的新格局。
在预测目标语言句子的下一个词时，利用attention接受到更多的信息。
- 首先，利用 s 1 s_1 s1向量与原句的每一个字的向量表示进行点积，相当于得到了一些打分。
Attention store:
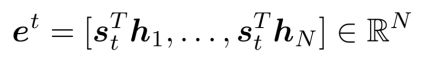
- 我们将上一步得到的打分通过求
softmax形成一个分布。经过变换后，这些打分总和为1，而且，其全部非负，可以看成概率分布。
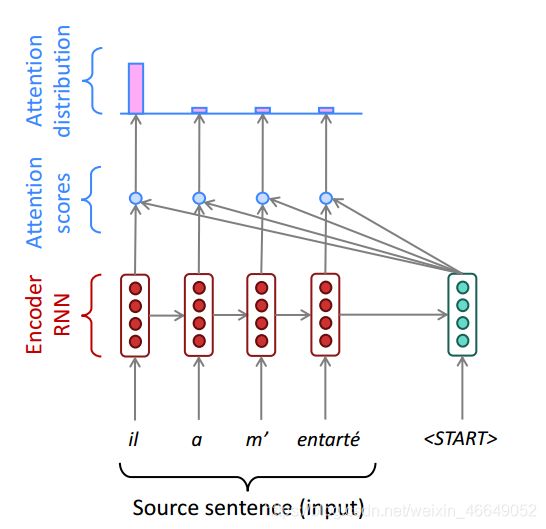
Attention distribution:
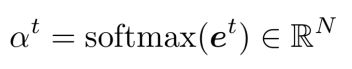
- 我们将原句的注意力向量表示用注意力打分进行加权平均就得到注意力输出向量Attention output。
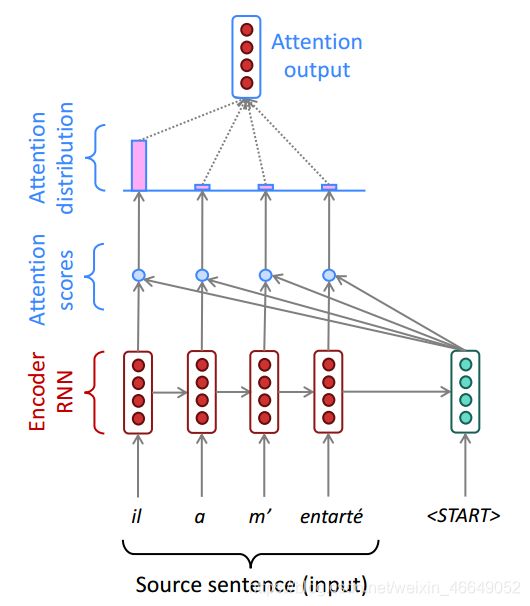
注意力打分加权平均表征：
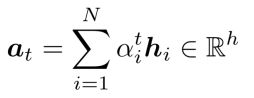
- 最后，Attention output能够帮助我们更好的预测下一个词，即将注意力输出与 s t s_t st拼接经过解码得到下一个字。
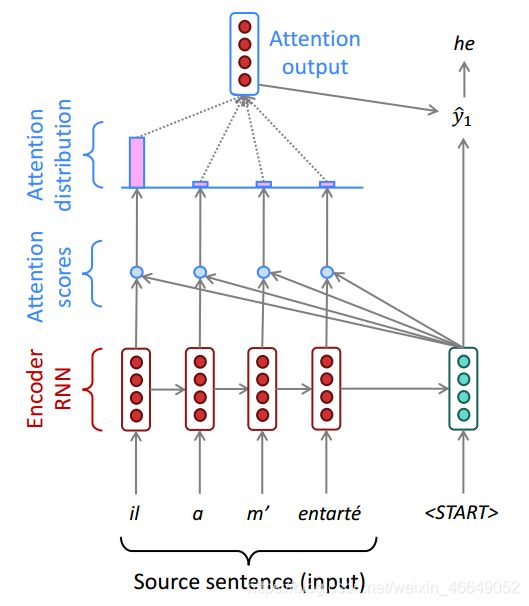
注意力输出与 s t s_t st拼接帮助解码：
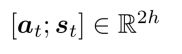
2.注意力的一般形式（三步曲）
注意力的一般定义:给定一组向量(key, value)键值对，以及一个向量query，注意力机制就是一种根据query与keys来计算values的加权平均的模块。
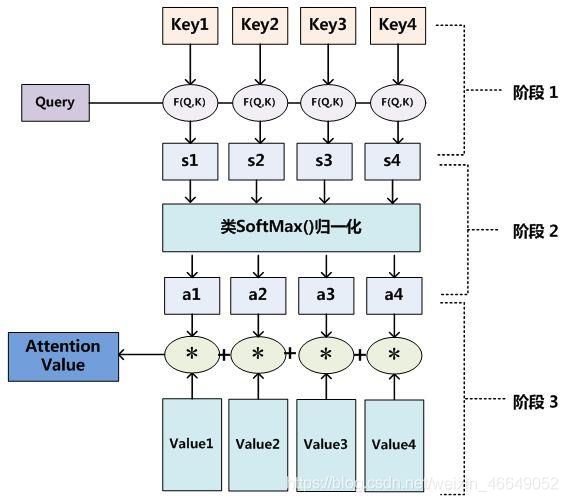
上面介绍的机器翻译模型中的attention机制打分是基于点积的。下面介绍attention机制的其他写法。常用的注意力打分方法有3种：
- 点积注意力(dot-product attention) :
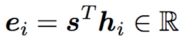
- 乘法注意力(multiplicative attention):
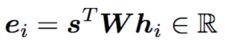
引入可学习的 W W W元素，使得attention机制更加匹配下游任务。 - 加法注意力(additive attention):
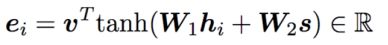
把query与key都引入到全连接层，通过引入一个额外的向量进行点积，最后形成一个attention打分。
3. transformer中的自注意力机制—Self.Attention
下面我们考虑一个问题：注意力机制是否可以得到一个句子的向量表征？这里就引出自注意力机制，通过自己注意自己，来更新句子每个词的向量表征。
自注意力机制建模句子表征的过程为：从单个字角度:e.g：it_的向量表征与句子中的所有词之间计算注意力，由此更新其向量表征。过程如下：
- 首先对Query、key与value均乘以一个参数矩阵
q i = h i W Q k i = h i W K v i = h i W V q_i=h_iW_Q\\k_i=h_iW_K\\v_i=h_iW_V qi=hiWQki=hiWKvi=hiWV - 假设
it_在句子的第 i i i个位置，那么它在第 j j j个位置的注意力打分为：
e i , j = q i T k j e_{i,j}=q_i^Tk_j ei,j=qiTkj - 通过softmax归一化成概率分布
α i = s o f t m a x ( [ e i , 1 , . . . , e i , T ] ) \alpha_i=softmax([e_{i,1},...,e_{i,T}]) αi=softmax([ei,1,...,ei,T]) - 通过注意力打分的分布，我们对value进行加权平均，然后再经过一个线性层输出 h i ′ h_i^{'} hi′， h i ′ h_i^{'} hi′正是更新后的
it_向量表征
h i ′ = ( ∑ α i , j v j ) W O h_i^{'}=(\sum{\alpha_{i,j}v_j})W_O hi′=(∑αi,jvj)WO
it_为Query，句子中的其他词为key与value
注意力机制通过操作实现了句子中词语两两间的交互。当然，在实现的过程中，不可能对句子中的每一个字都重复进行上面运算，这个非常低效。实际实现的过程中，需要通过矩阵的计算来使得整个句子直接完成两两之间的注意力的计算。整个句子的一次self-attention的过程如下：
- 假设句子现有表征记为 H = [ h 1 , . . . , h T ] H=[h_1,...,h_T] H=[h1,...,hT]，首先对Query、key与value均乘以一个参数矩阵
= = = = _\\ = _\\ = _ Q=HWQK=HWKV=HWV - 然后进行注意力打分
E = ( 转 置 ) E = ^(转置) E=QKT(转置) - 通过softmax归一化成概率分布
= ( ) = () Attn=Softmax(E) - 通过注意力打分的分布，我们对value进行加权平均
′ = ⋅ ^{'}= · H′=Attn⋅V
4. transformer的多头注意力机制
多头机制（multi-head attention）是BERT网络结构当中使用的网络优化技巧。它的思想是：使用不同的head关注不同的上下文依赖模式，类似于模型集成效应。
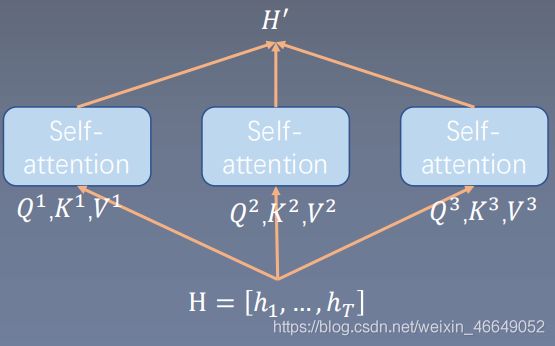
将网络的输入分成多个支，分别做注意力机制，最后将每支的结果进行拼接得到 H ′ H^{'} H′。
= i , = , = , i , ′ = ( ) ′ = [ 1 , ′ , 2 , ′ , … , , ′ ] O _ = _{i,} \\_ = _{,}\\ _ = _{,}\\ ^{i,′} = (_^{^} )\\ ′ = [^{1,′} , ^{2,′} , … , ^{,′} ]_O Qi=HWi,QKi=HWi,KVi=HWi,VHi,′=Softmax(QiKiT)ViH′=[H1,′,H2,′,…,HN,′]WO
5. scaling
scaling是transformer中又一模型优化技巧（Scaled dot-product attention）。即在计算attention分数时除以因子 d k \sqrt{d_k} dk，一般在transformer中取的是向量在每个head中的维度，一般 d k d_k dk为64。
= i , = , = , i , ′ = ( d k ) ′ = [ 1 , ′ , 2 , ′ , … , , ′ ] O _ = _{i,} \\_ = _{,}\\ _ = _{,}\\ ^{i,′} = (\frac{_^{^}}{\sqrt{d_k}})\\ ′ = [^{1,′} , ^{2,′} , … , ^{,′} ]_O Qi=HWi,QKi=HWi,KVi=HWi,VHi,′=Softmax(dkQiKiT)ViH′=[H1,′,H2,′,…,HN,′]WO
作用:模型维度较高的时候，向量点乘结果会比较大，这个时候由于经过了softmax，梯度会变小,训练会不稳定。除以因子 d k \sqrt{d_k} dk可以改善梯度不稳定的问题。
6. 模型优化技巧：残差连接
残差连接在CV领域无处不在，transformer中也存在模型优化技巧—残差连接。
残差链接的意义在于：
- 解决深度网络的梯度消失问题
- 改变损失函数形状，使得损失函数更加平滑，方便优化损失函数
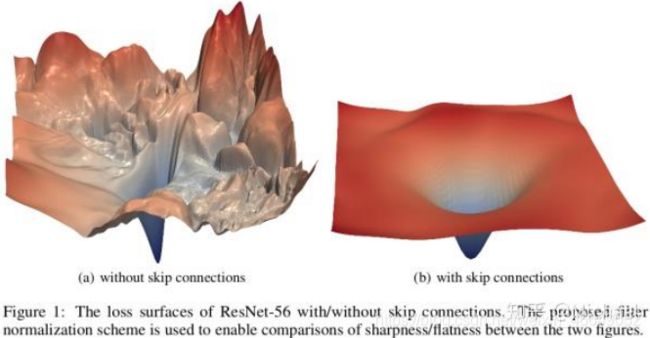
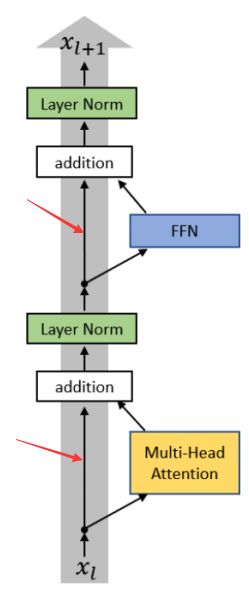
上图两部分均存在残差连接
H l + 1 = H l + l a y e r ( H l ) H^{l+1} =H^l+ layer (H^l ) Hl+1=Hl+layer(Hl)
三、BERT其他结构特性
1.BERT模型中的位置编码
一个Embedding层与多个self.Attention层是否能够组成一个NLP网络？答案是不行的。这就涉及到自注意力机制的辅助模块。首先第一个模块就是位置编码。
如果，我们将两个词was_与streets_的顺序调换，经过公式计算，并不会对其注意力打分有影响。
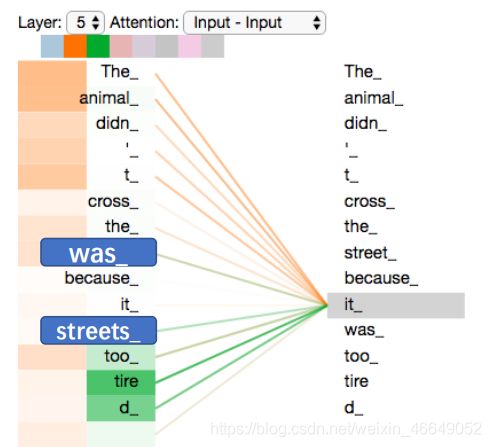
这说明我们现有的自注意力机制没有反映到句子序列的前后顺序信息。但是句子的顺序信息在自然语言处理当中应该是非常重要的，这就需要位置编码（Position encoding）用来表示位置信息。下面介绍位置编码。
位置编码形式为：
- p i ∈ R d , f o r i ∈ 1 , 2 , . . . , T p_i∈R^d,for i ∈ {1,2,...,T} pi∈Rd,fori∈1,2,...,T
位置编码的位置为：
-
可以加在Embedding层
-
也可以每层都加
位置编码的具体形式为: -
正余弦位置编码
通过给正余弦不同的周期达到区分位置的效果，transforms中使用了这种编码。
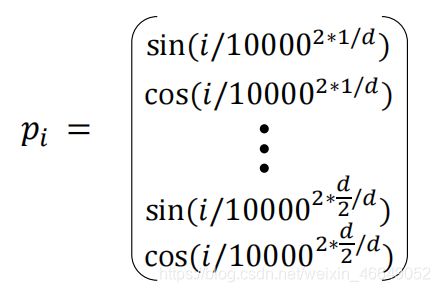
下面展示位置编码与句子位置之间的曲线关系
随着句子维度的增加，周期会逐渐增长。p_i 的不同维度，从1到768， 使用不同频率的正弦、余弦函数生成，然后和对应的位置的词向量相加。 这样设置其实是使得长度为T的序列，每个位置上的位置编码 p_i 都是不一样的。
-
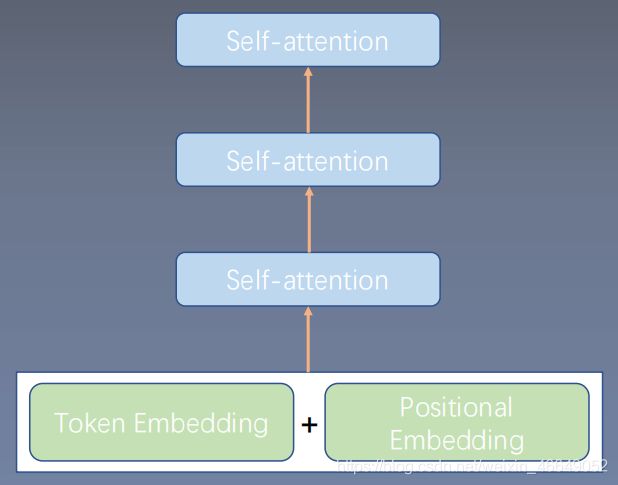
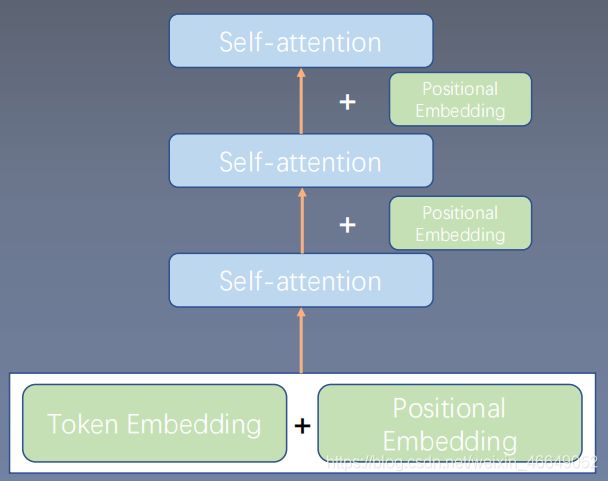
学习驱动的位置编码
p i p_i pi随机初始化，同模型一起学习。BERT模型中采用了这种位置编码。
2. BERT中的全连接层与非线性激活函数
上述工作是对句子中不同词之间的依赖进行建模，将该网络映射到更加高维的空间或者表达更加复杂的语义还有做，所以，我们可以增加一层全连接层，并给与非线性变换。这个正是BERT中的全连接层与非线性激活函数的作用。
增加全连接层后，公式为：
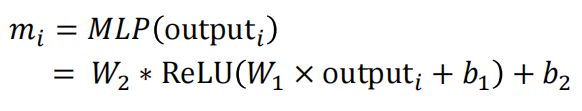
- 注意这里的操作是单点的(pointwise): m_i只由output_i决定,而不接收句子中其他信息。
后续，人们研究将不平滑的ReLU转化成平滑的ReLU，即GELU。GELU的一个特点是当输出为负数时，导数很大概率不为0。
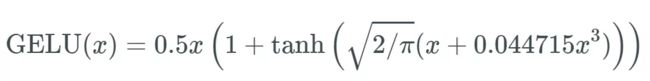
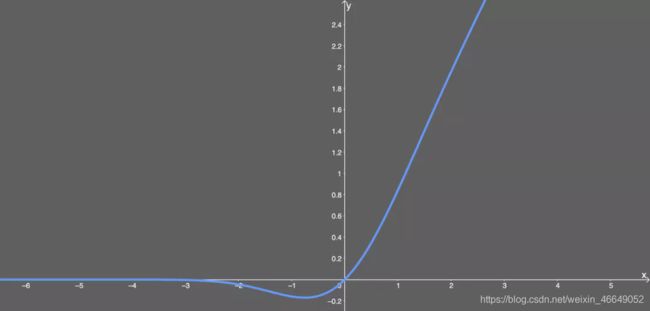
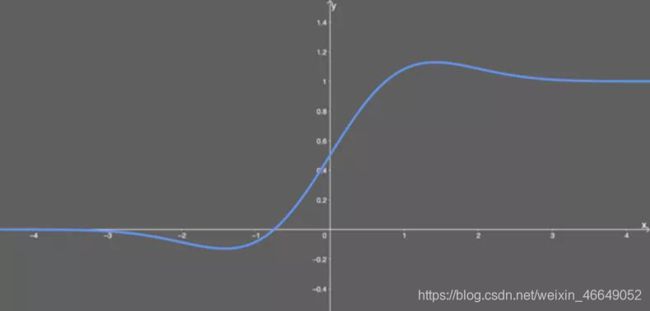
3. 层归一化—LayerNormalization
层归一化是transformer中需要的另一模型优化技巧:LayerNormalization。层归一化是对每一个向量单独求均值 μ \mu μ与方差 σ \sigma σ。
x ′ = x − μ σ + ϵ ∗ γ + β x^{'}=\frac{x-\mu}{\sqrt{\sigma}+\epsilon}*\gamma+\beta x′=σ+ϵx−μ∗γ+β
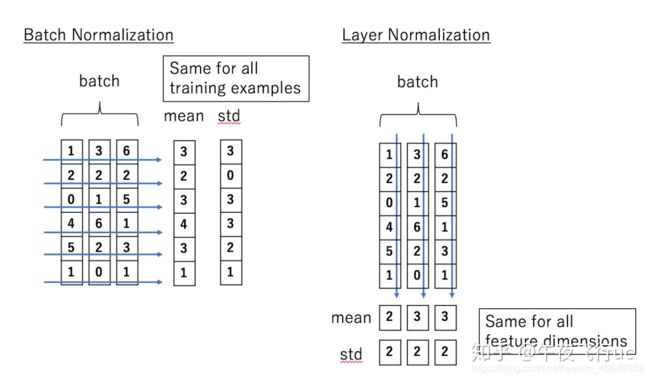
层归一化的意义：
- 与残差连接的作用类似:损失函数landscape（形状）变得平滑了
- 梯度的方差变小了，模型训练更加稳定
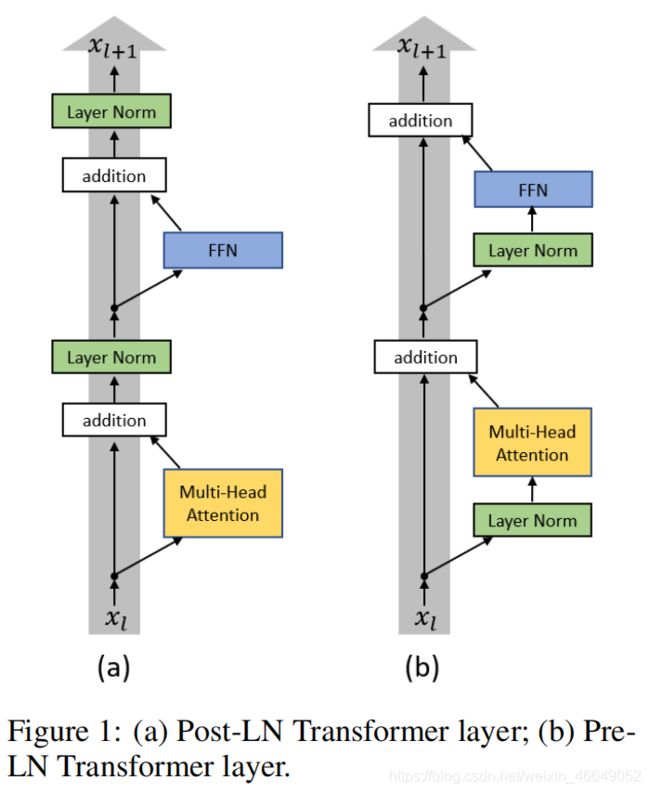
层归一化的位置也很重要。2019-2020年，微软研究了层归一化位置对模型的影响：
- 对于post-LN，最后一层的参数的梯度满足:
- 对于pre-LN，则为∶
AutoTrans提出采用自动机器学习的方法寻找layerNorm的最优位置组合。
如果对您有帮助，麻烦点赞关注，这真的对我很重要！！！如果需要互关，请评论或者私信！
