Datawhale 6月学习——图神经网络：基于GNN的节点预测任务及边预测任务

前情回顾

1. 图神经网络：图数据表示及应用
2. 图神经网络：消息传递图神经网络
3. 图神经网络：基于GNN的节点表征学习

1 节点预测任务

1.1 任务简述

通过构造一个数据完整存于内存的数据集类，并建立一个多层的图神经网络，来实现节点预测节点预测

1.2 数据完整存于内存的数据集类

所谓数据完整存于内存的数据集类，是指

对于占用内存有限的数据集，可以将整个数据集的数据都存储到内存里。

本部分主要是理解InMemory数据集类及学会覆写PyG的InMemoryDataset数据集类。
事实上，通过阅读源码可以发现，torch_geometric.datasets中的绝大部分数据集，都是通过覆写InMemoryDataset实现的。

PyG定义了使用数据的一般过程：

1. 从网络上下载数据原始文件；
2. 对数据原始文件做处理，为每一个图样本生成一个**Data对象**；
3. 对每一个Data对象执行数据处理，使其转换成新的Data对象；
4. 过滤Data对象；
5. 保存Data对象到文件；
6. 获取Data对象，在每一次获取Data对象时，都先对Data对象做数据变换（于是获取到的是数据变换后的Data对象）。

简单覆写流程需要覆写raw_file_names，processed_file_names，download，porcess等方法，具体为

• 在raw_file_names属性方法里，写上数据集原始文件有哪些，在此例子中有some_file_1, some_file_2等。
• 在processed_file_names属性方法里，处理过的数据要保存在哪些文件里，在此例子中只有data.pt。
• 在download方法里，我们实现下载数据到self.raw_dir文件夹的逻辑。
• 在process方法里，我们实现数据处理的逻辑：
  • 首先，我们从数据集原始文件中读取样本并生成Data对象，所有样本的Data对象保存在列表data_list中。
  • 其次，如果要对数据做过滤的话，我们执行数据过滤的过程。
  • 接着，如果要对数据做处理的话，我们执行数据处理的过程。
  • 最后，我们保存处理好的数据到文件。但由于python保存一个巨大的列表是相当慢的，我们需要先将所有Data对象合并成一个巨大的Data对象再保存。collate()函数接收一个列表的Data对象，返回合并后的Data对象以及用于从合并后的Data对象重构各个原始Data对象的切片字典slices。最后我们将这个巨大的Data对象和切片字典slices保存到文件。

为了方便后面进行节点预测任务，此处附上教程提供的PlanetoidPubMed数据集类代码，数据集描述可见Planetoid官方文档：torch_geometric.datasets.Planetoid

import os.path as osp

import torch
from torch_geometric.data import (InMemoryDataset, download_url)
from torch_geometric.io import read_planetoid_data

class PlanetoidPubMed(InMemoryDataset):
    r""" 节点代表文章，边代表引用关系。
   		 训练、验证和测试的划分通过二进制掩码给出。
    参数:
        root (string): 存储数据集的文件夹的路径
        transform (callable, optional): 数据转换函数，每一次获取数据时被调用。
        pre_transform (callable, optional): 数据转换函数，数据保存到文件前被调用。
    """

    url = 'https://github.com/kimiyoung/planetoid/raw/master/data'
    # url = 'https://gitee.com/rongqinchen/planetoid/raw/master/data'
    # 如果github的链接不可用，请使用gitee的链接

    def __init__(self, root, transform=None, pre_transform=None):

        super(PlanetoidPubMed, self).__init__(root, transform, pre_transform)
        self.data, self.slices = torch.load(self.processed_paths[0])

    @property
    def raw_dir(self):
        return osp.join(self.root, 'raw')

    @property
    def processed_dir(self):
        return osp.join(self.root, 'processed')

    @property
    def raw_file_names(self):
        names = ['x', 'tx', 'allx', 'y', 'ty', 'ally', 'graph', 'test.index']
        return ['ind.pubmed.{}'.format(name) for name in names]

    @property
    def processed_file_names(self):
        return 'data.pt'

    def download(self):
        for name in self.raw_file_names:
            download_url('{}/{}'.format(self.url, name), self.raw_dir)

    def process(self):
        data = read_planetoid_data(self.raw_dir, 'pubmed')
        data = data if self.pre_transform is None else self.pre_transform(data)
        torch.save(self.collate([data]), self.processed_paths[0])

    def __repr__(self):
        return '{}()'.format(self.name)

1.3 构建多层GNN网络

1.3.1 多层GAT网络

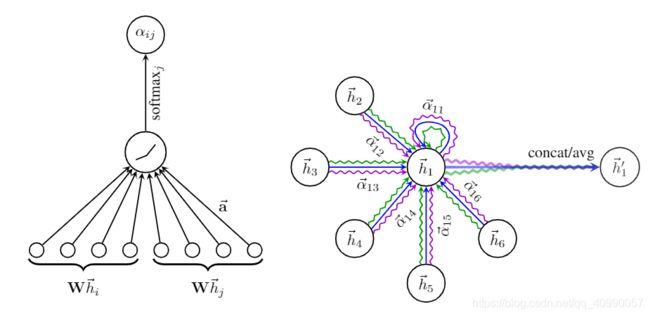
在上一节中，我们了解了几种常用的图卷积层模型，包括图卷积网络GAT

GAT，Graph Attention Networks，图注意网络，定义来源于论文Graph Attention Networks，引入了attention机制。

这里重定义一个GAT图神经网络，使其能够通过参数来定义GATConv的层数，以及每一层GATConv的out_channels，使用了torch_geometric.nn.Sequential容器，这个容器的操作可见于官方文档。
代码如下：

class GAT(torch.nn.Module):
    def __init__(self, num_features, hidden_channels_list, num_classes):
        super(GAT, self).__init__()
        torch.manual_seed(12345)
        hns = [num_features] + hidden_channels_list
        conv_list = []
        for idx in range(len(hidden_channels_list)):
            conv_list.append((GATConv(hns[idx], hns[idx+1]), 'x, edge_index -> x'))
            conv_list.append(ReLU(inplace=True),)

        self.convseq = Sequential('x, edge_index', conv_list)
        self.linear = Linear(hidden_channels_list[-1], num_classes)

    def forward(self, x, edge_index):
        x = self.convseq(x, edge_index)
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.linear(x)
        return x

这个网络由若干个GATConv层组成，hidden_channels_list传入组成这个网络的每个GATConv隐层的单元数。

1.3.2 多层GCN网络（作业）

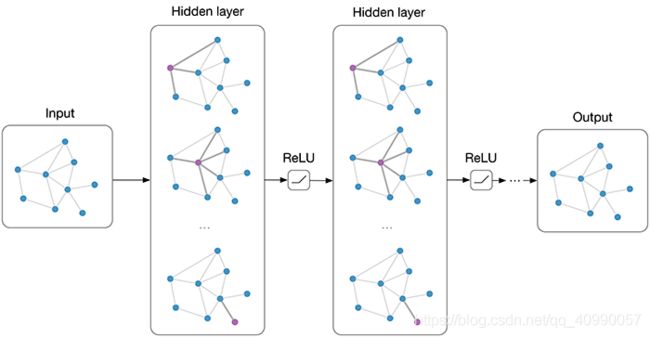
GCN的简单回顾

GCN，Graph Convolutional Networks，图卷积神经网络，定义来源于Semi-supervised Classification with Graph Convolutional Network，在hidden layers上实现消息的逐层传播。（图片来源于Graph Convolutional Networks——THOMAS KIPF）

同理可以构建如下

class GCN(torch.nn.Module):
    def __init__(self, num_features, hidden_channels_list, num_classes):
        super(GCN, self).__init__()
        torch.manual_seed(12345)
        hns = [num_features] + hidden_channels_list
        conv_list = []
        for idx in range(len(hidden_channels_list)):
            conv_list.append((GCNConv(hns[idx], hns[idx+1]), 'x, edge_index -> x'))
            conv_list.append(ReLU(inplace=True),)

        self.convseq = Sequential('x, edge_index', conv_list)
        self.linear = Linear(hidden_channels_list[-1], num_classes)

    def forward(self, x, edge_index):
        x = self.convseq(x, edge_index)
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.linear(x)
        return x

1.3.3 多层GraphSAGE网络（作业）

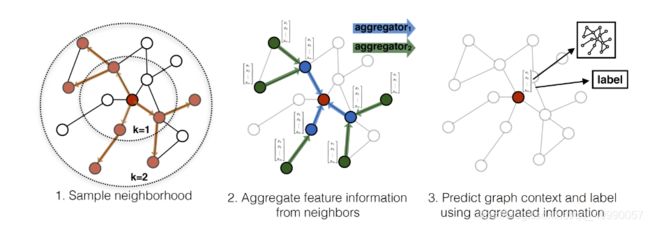
GraphSAGE的简单回顾

GraphSAGE（Graph SAmple and aggreGatE）是一种归纳学习框架，来源于论文Inductive Representation Learning on Large Graphs。

同理可以构建如下

class SAGE(torch.nn.Module):
    def __init__(self, num_features, hidden_channels_list, num_classes):
        super(SAGE, self).__init__()
        torch.manual_seed(12345)
        hns = [num_features] + hidden_channels_list
        conv_list = []
        for idx in range(len(hidden_channels_list)):
            conv_list.append((SAGEConv(hns[idx], hns[idx+1]), 'x, edge_index -> x'))
            conv_list.append(ReLU(inplace=True),)

        self.convseq = Sequential('x, edge_index', conv_list)
        self.linear = Linear(hidden_channels_list[-1], num_classes)

    def forward(self, x, edge_index):
        x = self.convseq(x, edge_index)
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.linear(x)
        return x

1.4 节点预测任务（作业）

1.4.1 两个隐层的图神经网络实例化及节点预测

以两个隐层，且单元数为200、100，实例化1.3节中定义的GAT、GCN、GraphSAGE网络，并在1.2节的数据集上进行节点预测。
实例化代码如下（以GCN为例）

dataset = PlanetoidPubMed(root="data/PlantoidPubMed")
data = dataset[0]

model = GCN(num_features = data.num_features, hidden_channels_list=[200,100], num_classes = dataset.num_classes)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
criterion = torch.nn.CrossEntropyLoss()

训练及测试代码如下

def train():
      model.train()
      optimizer.zero_grad()  # Clear gradients.
      out = model(data.x, data.edge_index)  # Perform a single forward pass.
      loss = criterion(out[data.train_mask], data.y[data.train_mask])  # Compute the loss solely based on the training nodes.
      loss.backward()  # Derive gradients.
      optimizer.step()  # Update parameters based on gradients.
      return loss

df = pd.DataFrame(columns = ["Loss"])
df.index.name = "Epoch"
for epoch in range(1, 51):
    loss = train()
    df.loc[epoch] = loss.item()

def test():
    model.eval()
    out = model(data.x, data.edge_index)
    pred = out.argmax(dim=1)  # Use the class with highest probability.
    test_correct = pred[data.test_mask] == data.y[data.test_mask]  # Check against ground-truth labels.
    test_acc = int(test_correct.sum()) / int(data.test_mask.sum())  # Derive ratio of correct predictions.
    return test_acc

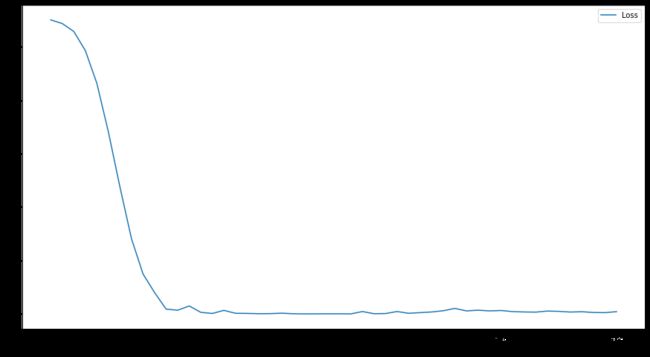
三者的训练过程中损失函数的变化情况如下

• GAT（200epoch）
• GCN（50epoch）
• GraphSAGE（50epoch）
  

可以看出，三者的收敛速度都很快。
在测试集上的准确率分别为

• GAT 74.6%
• GCN 78.7%
• GraphSAGE 75.1%

1.4.3 三个隐层的图神经网络实例化及节点预测

以三个隐层，且单元数为200，100、50，实例化1.3节中定义的GAT、GCN、GraphSAGE网络，并在1.2节的数据集上进行节点预测，代码与1.4.2节类似。
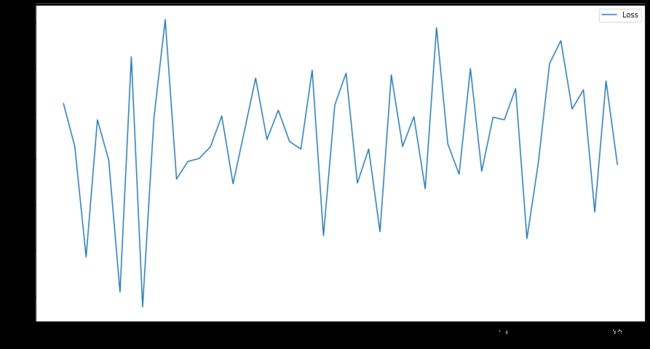
计算时间明显边长，损失函数情况如下

• GAT（50epoch）
  

• GCN（50epoch）
  

• GraphSAGE（50epoch）
  

50epoch内均未收敛
在测试集上的准确率分别为

• GAT 40.7%
• GCN 41.3%
• GraphSAGE 41.9%

效果均不如两隐层网络。
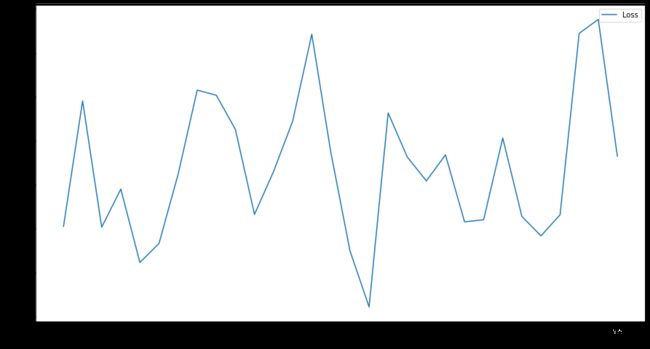
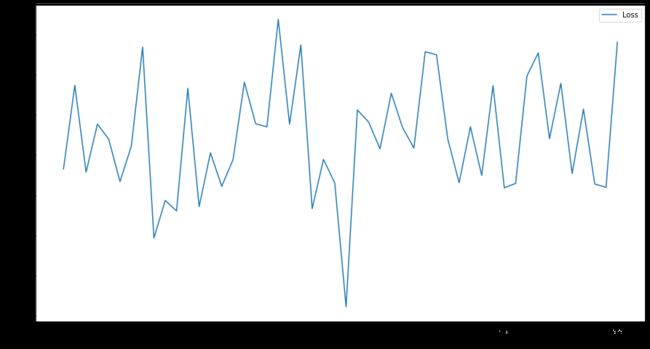
为初步探讨是否为隐层单元数影响，另外对GAT网络的三个隐层单元分别设为（200，150，100）和（400，200，100），测试如下

• （200，150，100）
  
• （400，200，100）
  

50epoch内均震荡
测试集上准确率：

• （200，150，100）：40.2%
• （400，200，100）：18.0%

效果均不如二隐层GAT，故并非隐层数越多越好；且并非单元数越多越好，在此试验中，单元数增多，反而准确率下降。
后续可以进行参数寻优，确定最合适的隐层数和隐层单元数。

2 边预测任务

2.1 任务简述

边预测任务是另一类图神经网络常见任务，目标是预测两个节点之间是否存在边。
对于此类任务，由于我们拿到手里的图edge_index中存储的都是有连接关系的节点对，所以我们需要进行处理，提取没有连接关系的节点对，才能完成这类任务。

边预测任务，目标是预测两个节点之间是否存在边。拿到一个图数据集，我们有节点属性x，边端点edge_index。edge_index存储的便是正样本。为了构建边预测任务，我们需要生成一些负样本，即采样一些不存在边的节点对作为负样本边，正负样本数量应平衡。此外要将样本分为训练集、验证集和测试集三个集合。

PyG中为我们提供了现成的采样负样本边的方法，train_test_split_edges(data, val_ratio=0.05, test_ratio=0.1)，并将正负样本分成训练集、验证集和测试集三个集合。

训练集要包含边的正向与反向，验证集与测试集都只包含了边的一个方向，因为，训练集用于训练，训练时一条边的两个端点要互传信息，只考虑一个方向的话，只能由一个端点传信息给另一个端点，而验证集与测试集的边用于衡量检验边预测的准确性，只需考虑一个方向的边即可。

2.2 边预测任务实现

2.2.1 神经网络的构造

神经网络构造源码如下

import torch
from torch_geometric.nn import GCNConv

class Net(torch.nn.Module):
    def __init__(self, in_channels, out_channels):
        super(Net, self).__init__()
        self.conv1 = GCNConv(in_channels, 128)
        self.conv2 = GCNConv(128, out_channels)

    def encode(self, x, edge_index):
        x = self.conv1(x, edge_index)
        x = x.relu()
        return self.conv2(x, edge_index)

    def decode(self, z, pos_edge_index, neg_edge_index):
        edge_index = torch.cat([pos_edge_index, neg_edge_index], dim=-1)
        return (z[edge_index[0]] * z[edge_index[1]]).sum(dim=-1)

    def decode_all(self, z):
        prob_adj = z @ z.t()
        return (prob_adj > 0).nonzero(as_tuple=False).t()

用于做边预测的神经网络主要由两部分组成：其一是编码（encode），它与我们前面介绍的节点表征生成是一样的；其二是解码（decode），它根据边两端节点的表征生成边为真的几率（odds）。
可以看到，该神经网络编码部分含两个卷积层，一个ReLU层；解码部分首先将正负样本拼接，再对output_channel的计算结果进行加和求解。

2.2.2 神经网络的训练（作业）

定义单个epoch的训练过程

def train(data, model, optimizer):
    model.train()

    neg_edge_index = negative_sampling(
        edge_index=data.train_pos_edge_index,
        num_nodes=data.num_nodes,
        num_neg_samples=data.train_pos_edge_index.size(1))

    optimizer.zero_grad()
    z = model.encode(data.x, data.train_pos_edge_index)
    link_logits = model.decode(z, data.train_pos_edge_index, neg_edge_index)
    link_labels = get_link_labels(data.train_pos_edge_index, neg_edge_index).to(data.x.device)
    loss = F.binary_cross_entropy_with_logits(link_logits, link_labels)
    loss.backward()
    optimizer.step()

    return loss

在训练开始时，首先对正负样本进行采样。

作业：我们以data.train_pos_edge_index为实际参数来进行训练集负样本采样，但这样采样得到的负样本可能包含一些验证集的正样本与测试集的正样本，即可能将真实的正样本标记为负样本，由此会产生冲突。但我们还是这么做，这是为什么？

这一步骤是为了使正负样本均衡，保证训练效果。通常，存在边的节点对的数量往往少于不存在边的节点对的数量，但有时未必，故会不可避免地采集到验证集和测试集的正样本。每个epoch都进行正负样本采样，采样到的样本数量与训练集正样本相同，但不同epoch中采样到的样本是不同的。这样做，我们既能实现类别数量平衡，又能实现增加训练集负样本的多样性。

定义单个epoch的测试过程（正负样本解码，与真实标签比较）

def test(data, model):
    model.eval()

    z = model.encode(data.x, data.train_pos_edge_index)

    results = []
    for prefix in ['val', 'test']:
        pos_edge_index = data[f'{prefix}_pos_edge_index']
        neg_edge_index = data[f'{prefix}_neg_edge_index']
        link_logits = model.decode(z, pos_edge_index, neg_edge_index)
        link_probs = link_logits.sigmoid()
        link_labels = get_link_labels(pos_edge_index, neg_edge_index)
        link_labels = link_labels.numpy()
        link_probs = link_probs.detach().numpy()
        results.append(roc_auc_score(link_labels, link_probs))
    return results

其中get_link_labels定义为，即正样本全为1，负样本全为0

def get_link_labels(pos_edge_index, neg_edge_index):
    num_links = pos_edge_index.size(1) + neg_edge_index.size(1)
    link_labels = torch.zeros(num_links, dtype=torch.float)
    link_labels[:pos_edge_index.size(1)] = 1.
    return link_labels

由于本次代码在colab平台上实现，不需要进行gpu，cpu的数据传输，故也不会进行数据类型的默认转换。在调用sklearn的roc_auc_score函数前，应确保link_labels和link_probs已变为numpy对象（不为torch.tensor），否则会出现报错

Can’t call numpy() on Tensor that requires grad. Use tensor.detach().numpy() instead.

上述代码中，

link_labels = link_labels.numpy()
link_probs = link_probs.detach().numpy()

完成了此操作。

2.2.3 边预测任务

调用主代码如下，流程包括包括数据集的导入，负样本采集，训练，测试。

import pandas as pd

#数据集导入及负样本生成
dataset = 'Cora'
dataset = Planetoid("data/Cora", dataset, transform=T.NormalizeFeatures())
data = dataset[0]
ground_truth_edge_index = data.edge_index
data.train_mask = data.val_mask = data.test_mask = data.y = None
data = train_test_split_edges(data)

#模型实例化及参数设置
model = Net(dataset.num_features, 64)
optimizer = torch.optim.Adam(params=model.parameters(), lr=0.01)

#训练及测试
df = pd.DataFrame(columns = ["Val","Test","Best_val"])
df.index.name = "Epoch"
    
best_val_auc = test_auc = 0
for epoch in range(1, 101):
    loss = train(data, model, optimizer)
    val_auc, tmp_test_auc = test(data, model)
    if val_auc > best_val_auc:
        best_val_auc = val_auc
        test_auc = tmp_test_auc
    df.loc[epoch,"Val"] = val_auc
    df.loc[epoch,"Test"] = test_auc
    df.loc[epoch,"Best_val"] = best_val_auc


z = model.encode(data.x, data.train_pos_edge_index)
final_edge_index = model.decode_all(z)

100个epoch中，验证集及测试集的ROC结果绘制如下

验证集上的最终ROC为94.4%，测试集上为90.5%。

2.3 用torch_geometric.nn.Sequential容器构造图神经网络实现边预测任务（作业）

2.3.1 神经网络的构造

使用torch_geometric.nn.Sequential构造如下

class NetSeq(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels_list, out_channels):
        super(NetSeq, self).__init__()
        torch.manual_seed(12345)
        hns = [in_channels] + hidden_channels_list
        conv_list = []
        for idx in range(len(hidden_channels_list)):
            conv_list.append((GCNConv(hns[idx], hns[idx+1]), 'x, edge_index -> x'))
            conv_list.append(ReLU(inplace=True),)

        self.convseq = Sequential('x, edge_index', conv_list)
        self.linear = Linear(hidden_channels_list[-1], out_channels)

    def encode(self, x, edge_index):
        x = self.convseq(x, edge_index)
        #x = x.relu()
        x = self.linear(x)
        return x

    def decode(self, z, pos_edge_index, neg_edge_index):
        edge_index = torch.cat([pos_edge_index, neg_edge_index], dim=-1) #正负样本衔接
        return (z[edge_index[0]] * z[edge_index[1]]).sum(dim=-1) #维度分析

    def decode_all(self, z):
        prob_adj = z @ z.t() #矩阵相乘
        return (prob_adj > 0).nonzero(as_tuple=False).t()

其中hidden_channels_list传入隐层单元数。每一个隐层由一个GCNConv和一个ReLU构成

2.3.2 神经网络的训练及边预测任务

设置隐层单元数为（100，50），实例化上述神经网络并训练，代码与2.2节类似，此处不重复。
100个epoch中，验证集及测试集的ROC结果绘制如下

验证集上的最佳ROC为70.8%，测试集上为67.4%。较单隐层网络（2.2）效果差。

设置隐层单元数为（60，30），100个epoch中，验证集及测试集的ROC结果绘制如下

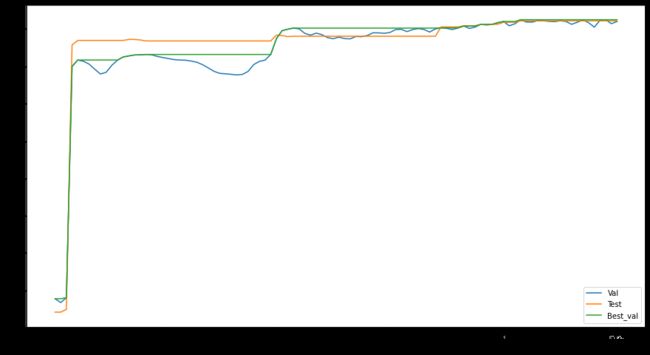
验证集上的最佳ROC为71.2%，测试集上为70.1%。效果优于（100，50），可见，亦非单元数越多越合适。
上述两例效果均显著差于2.2的单隐层网络，故并非隐层数越多越合适。

参考阅读

1. Datawhale组队学习