NNDL 实验六 卷积神经网络（3）LeNet实现MNIST

5.3 基于LeNet实现手写体数字识别实验

5.3.1 数据

5.3.1.1 数据集介绍

手写体数字识别是计算机视觉中最常用的图像分类任务，让计算机识别出给定图片中的手写体数字（0-9共10个数字）。由于手写体风格差异很大，因此手写体数字识别是具有一定难度的任务。

我们采用常用的手写数字识别数据集：MNIST数据集。
MNIST handwritten digit database, Yann LeCun, Corinna Cortes and Chris Burges
MNIST数据集是计算机视觉领域的经典入门数据集，包含了60,000个训练样本和10,000个测试样本。

这些数字已经过尺寸标准化并位于图像中心，图像是固定大小(28×28像素)。

LeNet-5虽然提出的时间比较早，但它是一个非常成功的神经网络模型。

基于LeNet-5的手写数字识别系统在20世纪90年代被美国很多银行使用，用来识别支票上面的手写数字。

导入数据集代码如下：

import json
import gzip
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
from torchvision.transforms import Compose, Resize, Normalize,ToTensor
import random
import torch.utils.data as data
import torch
import torch.nn.functional as F
import torch.nn as nn
from torch.nn.init import constant_, normal_, uniform_
import time
from torchsummary import summary
from thop import profile
import torch.optim as opt
from nndl import RunnerV3
import metric

# 打印并观察数据集分布情况
train_set, dev_set, test_set = json.load(gzip.open('./mnist.json.gz'))
train_images, train_labels = train_set[0][:1000], train_set[1][:1000]
dev_images, dev_labels = dev_set[0][:200], dev_set[1][:200]
test_images, test_labels = test_set[0][:200], test_set[1][:200]
train_set, dev_set, test_set = [train_images, train_labels], [dev_images, dev_labels], [test_images, test_labels]
print('Length of train/dev/test set:{}/{}/{}'.format(len(train_set[0]), len(dev_set[0]), len(test_set[0])))

运行结果：

Length of train/dev/test set:1000/200/200

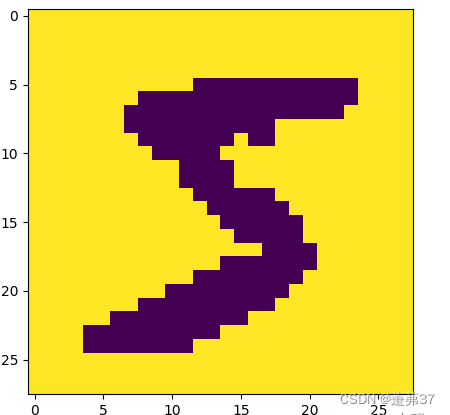
数据集第一张图片展示
代码：

import numpy as np
import matplotlib.pyplot as plt
import torch
import PIL.Image as Image
image, label = train_set[0][0], train_set[1][0]
image, label = np.array(image).astype('float32'), int(label)
# 原始图像数据为长度784的行向量，需要调整为[28,28]大小的图像
image = np.reshape(image, [28,28])
image = Image.fromarray(image.astype('uint8'), mode='L')
print("The number in the picture is {}".format(label))
plt.figure(figsize=(5, 5))
plt.imshow(image)
plt.savefig('conv-number5.pdf')
plt.show()

运行结果：

5.3.1.2 数据集导入

import torchvision.transforms as transforms

# 数据预处理
transforms = transforms.Compose([transforms.Resize(32),transforms.ToTensor(), transforms.Normalize(mean=[0.5], std=[0.5])])
import random
from torch.utils.data import Dataset,DataLoader

class MNIST_dataset(Dataset):
    def __init__(self, dataset, transforms, mode='train'):
        self.mode = mode
        self.transforms =transforms
        self.dataset = dataset

    def __getitem__(self, idx):
        # 获取图像和标签
        image, label = self.dataset[0][idx], self.dataset[1][idx]
        image, label = np.array(image).astype('float32'), int(label)
        image = np.reshape(image, [28,28])
        image = Image.fromarray(image.astype('uint8'), mode='L')
        image = self.transforms(image)

        return image, label

    def __len__(self):
        return len(self.dataset[0])
# 加载 mnist 数据集
train_dataset = MNIST_dataset(dataset=train_set, transforms=transforms, mode='train')
test_dataset = MNIST_dataset(dataset=test_set, transforms=transforms, mode='test')
dev_dataset = MNIST_dataset(dataset=dev_set, transforms=transforms, mode='dev')

5.3.2 模型构建

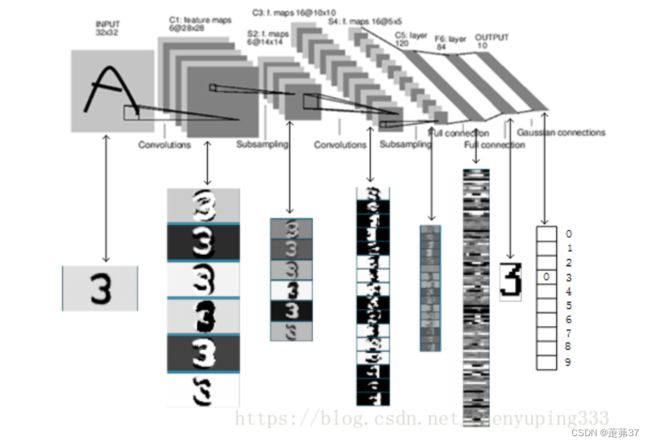
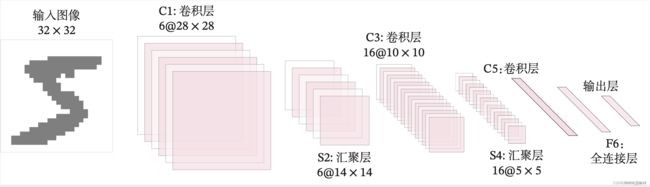
这里的LeNet-5和原始版本有4点不同：

1. C3层没有使用连接表来减少卷积数量。
2. 汇聚层使用了简单的平均汇聚，没有引入权重和偏置参数以及非线性激活函数。
3. 卷积层的激活函数使用ReLU函数。
4. 最后的输出层为一个全连接线性层。

网络共有7层，包含3个卷积层、2个汇聚层以及2个全连接层的简单卷积神经网络接，受输入图像大小为32×32=1024，输出对应10个类别的得分。

5.3.2.1使用自定义算子，构建LeNet-5模型

使用pytorch中的相应算子，构建LeNet-5模型

torch.nn.Conv2d()；torch.nn.MaxPool2d()；torch.nn.avg_pool2d()

Conv2d():

class Conv2D(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
        weight_attr = constant_(torch.empty(size=(out_channels, in_channels, kernel_size, kernel_size)),val=1.0)
        bias_attr = constant_(torch.empty(size=(out_channels,1)), val=0.0)
        super(Conv2D, self).__init__()
        # 创建卷积核
        self.weight = torch.nn.parameter.Parameter(weight_attr,requires_grad=True)
        # 创建偏置
        self.bias = torch.nn.parameter.Parameter(bias_attr,requires_grad=True)
        self.stride = stride
        self.padding = padding
        # 输入通道数
        self.in_channels = in_channels
        # 输出通道数
        self.out_channels = out_channels
 
    # 基础卷积运算
    def single_forward(self, X, weight):
        # 零填充
        new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
        new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
        u, v = weight.shape
        output_w = (new_X.shape[1] - u) // self.stride + 1
        output_h = (new_X.shape[2] - v) // self.stride + 1
        output = torch.zeros([X.shape[0], output_w, output_h])
        for i in range(0, output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = torch.sum(
                    new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * weight,
                    dim=[1, 2])
        return output
 
    def forward(self, inputs):
        """
        输入：
            - inputs：输入矩阵，shape=[B, D, M, N]
            - weights：P组二维卷积核，shape=[P, D, U, V]
            - bias：P个偏置，shape=[P, 1]
        """
        feature_maps = []
        # 进行多次多输入通道卷积运算
        p = 0
        for w, b in zip(self.weight, self.bias):  # P个(w,b),每次计算一个特征图Zp
            multi_outs = []
            # 循环计算每个输入特征图对应的卷积结果
            for i in range(self.in_channels):
                single = self.single_forward(inputs[:, i, :, :], w[i])
                multi_outs.append(single)
                # print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
            # 将所有卷积结果相加
            feature_map = torch.sum(torch.stack(multi_outs), dim=0) + b  # Zp
            feature_maps.append(feature_map)
            # print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
            p += 1
        # 将所有Zp进行堆叠
        out = torch.stack(feature_maps, 1)
        return out

Pool2D()：

class Pool2D(nn.Module):
    def __init__(self, size=(2, 2), mode='max', stride=1):
        super(Pool2D, self).__init__()
        # 汇聚方式
        self.mode = mode
        self.h, self.w = size
        self.stride = stride
 
    def forward(self, x):
        output_w = (x.shape[2] - self.w) // self.stride + 1
        output_h = (x.shape[3] - self.h) // self.stride + 1
        output = torch.zeros([x.shape[0], x.shape[1], output_w, output_h])
        # 汇聚
        for i in range(output.shape[2]):
            for j in range(output.shape[3]):
                # 最大汇聚
                if self.mode == 'max':
                    output[:, :, i, j] = torch.max(
                        x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h])
                # 平均汇聚
                elif self.mode == 'avg':
                    output[:, :, i, j] = torch.mean(
                        x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h],
                        dim=[2, 3])
 
        return output

class Model_LeNet(nn.Module):
    def __init__(self, in_channels, num_classes=10):
        super(Model_LeNet, self).__init__()
        # 卷积层：输出通道数为6，卷积核大小为5×5
        self.conv1 = Conv2D(in_channels=in_channels, out_channels=6, kernel_size=5)
        # 汇聚层：汇聚窗口为2×2，步长为2
        self.pool2 = Pool2D(size=(2,2), mode='max', stride=2)
        # 卷积层：输入通道数为6，输出通道数为16，卷积核大小为5×5，步长为1
        self.conv3 = Conv2D(in_channels=6, out_channels=16, kernel_size=5, stride=1)
        # 汇聚层：汇聚窗口为2×2，步长为2
        self.pool4 = Pool2D(size=(2,2), mode='avg', stride=2)
        # 卷积层：输入通道数为16，输出通道数为120，卷积核大小为5×5
        self.conv5 = Conv2D(in_channels=16, out_channels=120, kernel_size=5, stride=1)
        # 全连接层：输入神经元为120，输出神经元为84
        self.linear6 = nn.Linear(120, 84)
        # 全连接层：输入神经元为84，输出神经元为类别数
        self.linear7 = nn.Linear(84, num_classes)
 
    def forward(self, x):
        # C1：卷积层+激活函数
        output = F.relu(self.conv1(x))
        # S2：汇聚层
        output = self.pool2(output)
        # C3：卷积层+激活函数
        output = F.relu(self.conv3(output))
        # S4：汇聚层
        output = self.pool4(output)
        # C5：卷积层+激活函数
        output = F.relu(self.conv5(output))
        # 输入层将数据拉平[B,C,H,W] -> [B,CxHxW]
        output = torch.squeeze(output, dim=3)
        output = torch.squeeze(output, dim=2)
        # F6：全连接层
        output = F.relu(self.linear6(output))
        # F7：全连接层
        output = self.linear7(output)
        return output

5.3.2.2使用pytorch中的相应算子，构建LeNet-5模型

考虑到自定义的Conv2D和Pool2D算子中包含多个for循环，所以运算速度比较慢。飞桨框架中，针对卷积层算子和汇聚层算子进行了速度上的优化，这里基于paddle.nn.Conv2D、paddle.nn.MaxPool2D和paddle.nn.AvgPool2D构建LeNet-5模型，对比与上边实现的模型的运算速度。代码如下：

class Paddle_LeNet(nn.Module):
    def __init__(self, in_channels, num_classes=10):
        super(Paddle_LeNet, self).__init__()
        # 卷积层：输出通道数为6，卷积核大小为5*5
        self.conv1 = nn.Conv2d(in_channels=in_channels, out_channels=6, kernel_size=5)
        # 汇聚层：汇聚窗口为2*2，步长为2
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        # 卷积层：输入通道数为6，输出通道数为16，卷积核大小为5*5
        self.conv3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
        # 汇聚层：汇聚窗口为2*2，步长为2
        self.pool4 = nn.AvgPool2d(kernel_size=2, stride=2)
        # 卷积层：输入通道数为16，输出通道数为120，卷积核大小为5*5
        self.conv5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5)
        # 全连接层：输入神经元为120，输出神经元为84
        self.linear6 = nn.Linear(in_features=120, out_features=84)
        # 全连接层：输入神经元为84，输出神经元为类别数
        self.linear7 = nn.Linear(in_features=84, out_features=num_classes)
 
    def forward(self, x):
        # C1：卷积层+激活函数
        output = F.relu(self.conv1(x))
        # S2：汇聚层
        output = self.pool2(output)
        # C3：卷积层+激活函数
        output = F.relu(self.conv3(output))
        # S4：汇聚层
        output = self.pool4(output)
        # C5：卷积层+激活函数
        output = F.relu(self.conv5(output))
        # 输入层将数据拉平[B,C,H,W] -> [B,CxHxW]
        output = torch.squeeze(output, dim=3)
        output = torch.squeeze(output, dim=2)
        # F6：全连接层
        output = F.relu(self.linear6(output))
        # F7：全连接层
        output = self.linear7(output)
        return output

5.3.2.3 测试LeNet-5模型，构造一个形状为 [1,1,32,32]的输入数据送入网络，观察每一层特征图的形状变化。

# 这里用np.random创建一个随机数组作为输入数据
inputs = np.random.randn(*[1,1,32,32])
inputs = inputs.astype('float32')
 
# 创建Model_LeNet类的实例，指定模型名称和分类的类别数目
model = Model_LeNet(in_channels=1, num_classes=10)
# 通过调用LeNet从基类继承的sublayers()函数，查看LeNet中所包含的子层
c=[]
for a ,b in model.named_children():
    c.append(a)
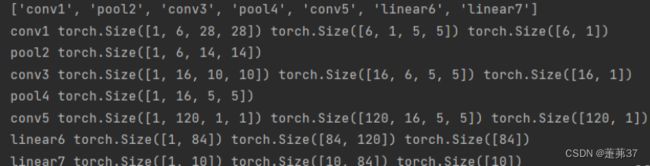
print(c)
x = torch.tensor(inputs)
for a,item in model.named_children():
    # item是LeNet类中的一个子层
    # 查看经过子层之后的输出数据形状
    try:
        x = item(x)
    except:
        # 如果是最后一个卷积层输出，需要展平后才可以送入全连接层
        x = torch.reshape(x, [x.shape[0], -1])
        x = item(x)
    d=[]
    e=[]
    for b,c in item.named_parameters():
        d.append(b)
        e.append(c)
    if len(e)==2:
        # 查看卷积和全连接层的数据和参数的形状，
        # 其中item.parameters()[0]是权重参数w，item.parameters()[1]是偏置参数b
        print(a, x.shape, e[0].shape,
                e[1].shape)
    else:
        # 汇聚层没有参数
        print(a, x.shape)

运行结果：
从输出结果看：

• 对于大小为32×32的单通道图像，先用6个大小为5×5的卷积核对其进行卷积运算，输出为6个28×28大小的特征图；
• 6个28×28大小的特征图经过大小为2×2，步长为2的汇聚层后，输出特征图的大小变为14×14；
• 6个14×14大小的特征图再经过16个大小为5×5的卷积核对其进行卷积运算，得到16个10×10大小的输出特征图；
• 16个10×10大小的特征图经过大小为2×2，步长为2的汇聚层后，输出特征图的大小变为5×5；
• 16个5×5大小的特征图再经过120个大小为5×5的卷积核对其进行卷积运算，得到120个1×1大小的输出特征图；
• 此时，将特征图展平成1维，则有120个像素点，经过输入神经元个数为120，输出神经元个数为84的全连接层后，输出的长度变为84。
• 再经过一个全连接层的计算，最终得到了长度为类别数的输出结果。

5.3.2.4 测试两个网络的运算速度。

# 这里用np.random创建一个随机数组作为测试数据
inputs = np.random.randn(*[1,1,32,32])
inputs = inputs.astype('float32')
x = torch.tensor(inputs)
 
# 创建Model_LeNet类的实例，指定模型名称和分类的类别数目
model = Model_LeNet(in_channels=1, num_classes=10)
# 创建Paddle_LeNet类的实例，指定模型名称和分类的类别数目
paddle_model = Paddle_LeNet(in_channels=1, num_classes=10)
 
# 计算Model_LeNet类的运算速度
model_time = 0
for i in range(60):
    strat_time = time.time()
    out = model(x)
    end_time = time.time()
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    model_time += (end_time - strat_time)
avg_model_time = model_time / 50
print('Model_LeNet speed:', avg_model_time, 's')
 
# 计算Paddle_LeNet类的运算速度
paddle_model_time = 0
for i in range(60):
    strat_time = time.time()
    paddle_out = paddle_model(x)
    end_time = time.time()
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    paddle_model_time += (end_time - strat_time)
avg_paddle_model_time = paddle_model_time / 50
 
print('Paddle_LeNet speed:', avg_paddle_model_time, 's')

运行结果：

5.3.2.5 令两个网络加载同样的权重，测试一下两个网络的输出结果是否一致。

# 这里用np.random创建一个随机数组作为测试数据
inputs = np.random.randn(*[1,1,32,32])
inputs = inputs.astype('float32')
x = torch.tensor(inputs)
 
# 创建Model_LeNet类的实例，指定模型名称和分类的类别数目
model = Model_LeNet(in_channels=1, num_classes=10)
# 获取网络的权重
params = model.state_dict()
# 自定义Conv2D算子的bias参数形状为[out_channels, 1]
# paddle API中Conv2D算子的bias参数形状为[out_channels]
# 需要进行调整后才可以赋值
for key in params:
    if 'bias' in key:
        params[key] = params[key].squeeze()
# 创建Paddle_LeNet类的实例，指定模型名称和分类的类别数目
paddle_model = Paddle_LeNet(in_channels=1, num_classes=10)
# 将Model_LeNet的权重参数赋予给Paddle_LeNet模型，保持两者一致
paddle_model.load_state_dict(params)
 
# 打印结果保留小数点后6位
torch.set_printoptions(6)
# 计算Model_LeNet的结果
output = model(x)
print('Model_LeNet output: ', output)
# 计算Paddle_LeNet的结果
paddle_output = paddle_model(x)
print('Paddle_LeNet output: ', paddle_output)

运行结果：

5.3.2.6 统计LeNet-5模型的参数量和计算量。

from torchsummary import summary
model = Torch_LeNet(in_channels=1, num_classes=10)
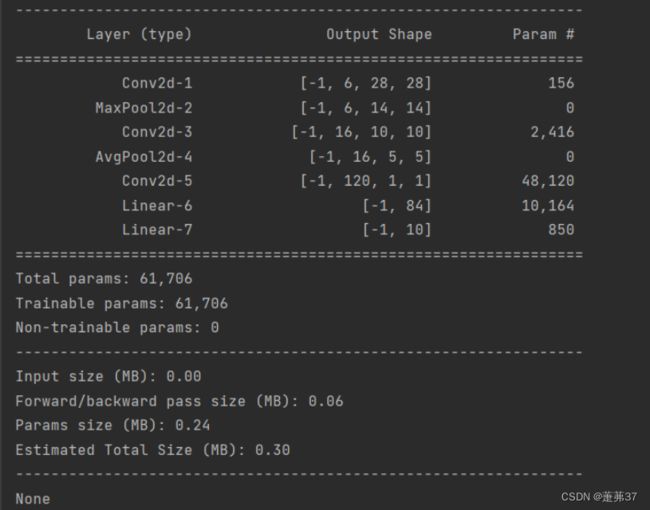
params_info = summary(model, (1, 32, 32))
print(params_info)

运行结果：

• 第一个卷积层的参数量为：6×1×5×5+6=156；
• 第二个卷积层的参数量为：16×6×5×5+16=2416；
• 第三个卷积层的参数量为：120×16×5×5+120=48120；
• 第一个全连接层的参数量为：120×84+84=10164；
• 第二个全连接层的参数量为：84×10+10=850；

所以，LeNet-5总的参数量为61706。

5.3.3 模型训练

使用交叉熵损失函数，并用随机梯度下降法作为优化器来训练LeNet-5网络。
用RunnerV3在训练集上训练5个epoch，并保存准确率最高的模型作为最佳模型。

torch.manual_seed(100)
# 学习率大小
lr = 0.1
# 批次大小
batch_size = 64
# 加载数据
 
 
train_loader = data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = data.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = data.DataLoader(test_dataset, batch_size=batch_size)
# 定义LeNet网络
# 自定义算子实现的LeNet-5
#model = Model_LeNet(in_channels=1, num_classes=10)
# 飞桨API实现的LeNet-5
model = Paddle_LeNet(in_channels=1, num_classes=10)
# 定义优化器
optimizer = opt.SGD(lr=lr, params=model.parameters())
# 定义损失函数
loss_fn = F.cross_entropy
# 定义评价指标
metric = Accuracy(is_logist=True)
# 实例化 RunnerV3 类，并传入训练配置。
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 启动训练
log_steps = 15
eval_steps = 15
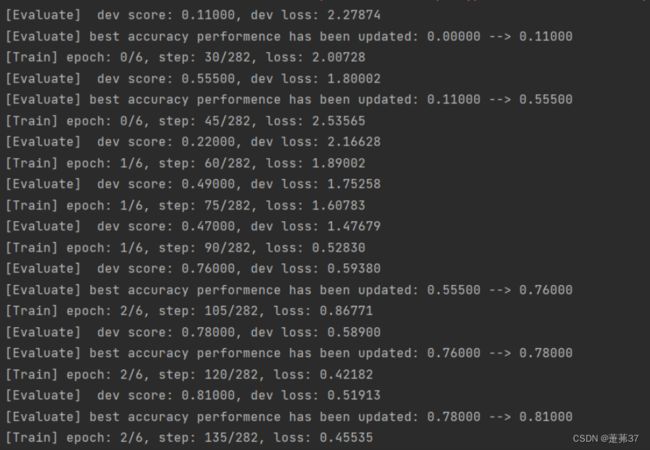
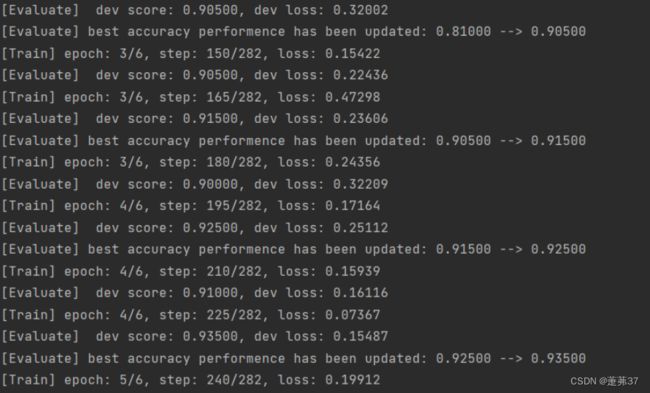
runner.train(train_loader, dev_loader, num_epochs=5, log_steps=log_steps,
            eval_steps=eval_steps, save_path="best_model.pdparams")

RunnerV3：

class RunnerV3(object):
    def __init__(self, model, optimizer, loss_fn, metric, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric  # 只用于计算评价指标
 
        # 记录训练过程中的评价指标变化情况
        self.dev_scores = []
 
        # 记录训练过程中的损失函数变化情况
        self.train_epoch_losses = []  # 一个epoch记录一次loss
        self.train_step_losses = []  # 一个step记录一次loss
        self.dev_losses = []
 
        # 记录全局最优指标
        self.best_score = 0
 
    def train(self, train_loader, dev_loader=None, **kwargs):
        # 将模型切换为训练模式
        self.model.train()
 
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_steps = kwargs.get("log_steps", 100)
        # 评价频率
        eval_steps = kwargs.get("eval_steps", 0)
 
        # 传入模型保存路径，如果没有传入值则默认为"best_model.pdparams"
        save_path = kwargs.get("save_path", "best_model.pdparams")
 
        custom_print_log = kwargs.get("custom_print_log", None)
 
        # 训练总的步数
        num_training_steps = num_epochs * len(train_loader)
 
        if eval_steps:
            if self.metric is None:
                raise RuntimeError('Error: Metric can not be None!')
            if dev_loader is None:
                raise RuntimeError('Error: dev_loader can not be None!')
 
        # 运行的step数目
        global_step = 0
 
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            # 用于统计训练集的损失
            total_loss = 0
            for step, data in enumerate(train_loader):
                X, y = data
                # 获取模型预测
                logits = self.model(X)
                loss = self.loss_fn(logits, y)  # 默认求mean
                total_loss += loss
 
                # 训练过程中，每个step的loss进行保存
                self.train_step_losses.append((global_step, loss.item()))
 
                if log_steps and global_step % log_steps == 0:
                    print(
                        f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")
 
                # 梯度反向传播，计算每个参数的梯度值
                loss.backward()
 
                if custom_print_log:
                    custom_print_log(self)
 
                # 小批量梯度下降进行参数更新
                self.optimizer.step()
                # 梯度归零
                self.optimizer.zero_grad()
 
                # 判断是否需要评价
                if eval_steps > 0 and global_step > 0 and \
                        (global_step % eval_steps == 0 or global_step == (num_training_steps - 1)):
 
                    dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)
                    print(f"[Evaluate]  dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}")
 
                    # 将模型切换为训练模式
                    self.model.train()
 
                    # 如果当前指标为最优指标，保存该模型
                    if dev_score > self.best_score:
                        self.save_model(save_path)
                        print(
                            f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")
                        self.best_score = dev_score
 
                global_step += 1
 
            # 当前epoch 训练loss累计值
            trn_loss = (total_loss / len(train_loader)).item()
            # epoch粒度的训练loss保存
            self.train_epoch_losses.append(trn_loss)
 
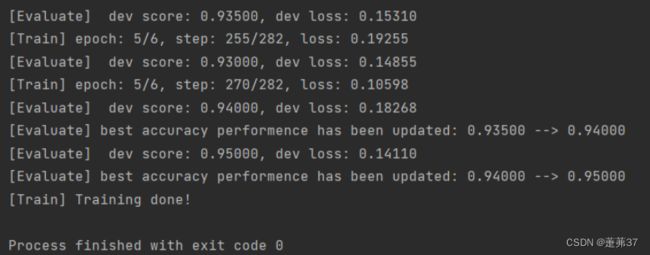
        print("[Train] Training done!")
 
    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def evaluate(self, dev_loader, **kwargs):
        assert self.metric is not None
 
        # 将模型设置为评估模式
        self.model.eval()
 
        global_step = kwargs.get("global_step", -1)
 
        # 用于统计训练集的损失
        total_loss = 0
 
        # 重置评价
        self.metric.reset()
 
        # 遍历验证集每个批次
        for batch_id, data in enumerate(dev_loader):
            X, y = data
 
            # 计算模型输出
            logits = self.model(X)
 
            # 计算损失函数
            loss = self.loss_fn(logits, y).item()
            # 累积损失
            total_loss += loss
 
            # 累积评价
            self.metric.update(logits, y)
 
        dev_loss = (total_loss / len(dev_loader))
        dev_score = self.metric.accumulate()
 
        # 记录验证集loss
        if global_step != -1:
            self.dev_losses.append((global_step, dev_loss))
            self.dev_scores.append(dev_score)
 
        return dev_score, dev_loss
 
    # 模型评估阶段，使用'paddle.no_grad()'控制不计算和存储梯度
    @torch.no_grad()
    def predict(self, x, **kwargs):
        # 将模型设置为评估模式
        self.model.eval()
        # 运行模型前向计算，得到预测值
        logits = self.model(x)
        return logits
 
    def save_model(self, save_path):
        torch.save(self.model.state_dict(), save_path)
 
    def load_model(self, model_path):
        state_dict = torch.load(model_path)
        self.model.load_state_dict(state_dict)

accuracy：

class Accuracy():
    def __init__(self, is_logist=True):
        """
        输入：
           - is_logist: outputs是logist还是激活后的值
        """
 
        # 用于统计正确的样本个数
        self.num_correct = 0
        # 用于统计样本的总数
        self.num_count = 0
 
        self.is_logist = is_logist
 
    def update(self, outputs, labels):
        """
        输入：
           - outputs: 预测值, shape=[N,class_num]
           - labels: 标签值, shape=[N,1]
        """
 
        # 判断是二分类任务还是多分类任务，shape[1]=1时为二分类任务，shape[1]>1时为多分类任务
        if outputs.shape[1] == 1:  # 二分类
            outputs = torch.squeeze(outputs, dim=-1)
            if self.is_logist:
                # logist判断是否大于0
                preds = torch.tensor((outputs >= 0), dtype=torch.float32)
            else:
                # 如果不是logist，判断每个概率值是否大于0.5，当大于0.5时，类别为1，否则类别为0
                preds = torch.tensor((outputs >= 0.5), dtype=torch.float32)
        else:
            # 多分类时，使用'torch.argmax'计算最大元素索引作为类别
            preds = torch.argmax(outputs, dim=1)
 
        # 获取本批数据中预测正确的样本个数
        labels = torch.squeeze(labels, dim=-1)
        batch_correct = torch.sum(torch.tensor(preds == labels, dtype=torch.float32)).numpy()
        batch_count = len(labels)
 
        # 更新num_correct 和 num_count
        self.num_correct += batch_correct
        self.num_count += batch_count
 
    def accumulate(self):
        # 使用累计的数据，计算总的指标
        if self.num_count == 0:
            return 0
        return self.num_correct / self.num_count
 
    def reset(self):
        # 重置正确的数目和总数
        self.num_correct = 0
        self.num_count = 0
 
    def name(self):
        return "Accuracy"

运行结果：
可视化观察训练集与验证集的损失变化情况。

# 可视化
def plot(runner, fig_name):
    plt.figure(figsize=(10, 5))
 
    plt.subplot(1, 2, 1)
    train_items = runner.train_step_losses[::30]
    train_steps = [x[0] for x in train_items]
    train_losses = [x[1] for x in train_items]
 
    plt.plot(train_steps, train_losses, color='#8E004D', label="Train loss")
    if runner.dev_losses[0][0] != -1:
        dev_steps = [x[0] for x in runner.dev_losses]
        dev_losses = [x[1] for x in runner.dev_losses]
        plt.plot(dev_steps, dev_losses, color='#E20079', linestyle='--', label="Dev loss")
    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='x-large')
    plt.xlabel("step", fontsize='x-large')
    plt.legend(loc='upper right', fontsize='x-large')
 
    plt.subplot(1, 2, 2)
    # 绘制评价准确率变化曲线
    if runner.dev_losses[0][0] != -1:
        plt.plot(dev_steps, runner.dev_scores,
                 color='#E20079', linestyle="--", label="Dev accuracy")
    else:
        plt.plot(list(range(len(runner.dev_scores))), runner.dev_scores,
                 color='#E20079', linestyle="--", label="Dev accuracy")
    # 绘制坐标轴和图例
    plt.ylabel("score", fontsize='x-large')
    plt.xlabel("step", fontsize='x-large')
    plt.legend(loc='lower right', fontsize='x-large')
 
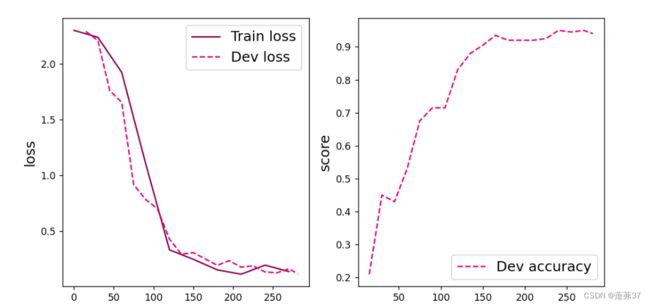
    plt.savefig(fig_name)
    plt.show()


plot(runner, 'cnn-loss1.pdf')

运行结果：

5.3.4 模型评价

使用测试数据对在训练过程中保存的最佳模型进行评价，观察模型在测试集上的准确率以及损失变化情况。

# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))

运行结果：

5.3.5 模型预测

同样地，我们也可以使用保存好的模型，对测试集中的某一个数据进行模型预测，观察模型效果。

# 获取测试集中第一条数
X, label = next(iter(test_loader))
logits = runner.predict(X)
# 多分类，使用softmax计算预测概率
pred = F.softmax(logits,dim=1)
print(pred.shape)
# 获取概率最大的类别
pred_class = torch.argmax(pred[2]).numpy()
print(pred_class)
label = label[2].numpy()
# 输出真实类别与预测类别
print("The true category is {} and the predicted category is {}".format(label, pred_class))
# 可视化图片
plt.figure(figsize=(2, 2))
image, label = test_set[0][2], test_set[1][2]
image= np.array(image).astype('float32')
image = np.reshape(image, [28,28])
image = Image.fromarray(image.astype('uint8'), mode='L')
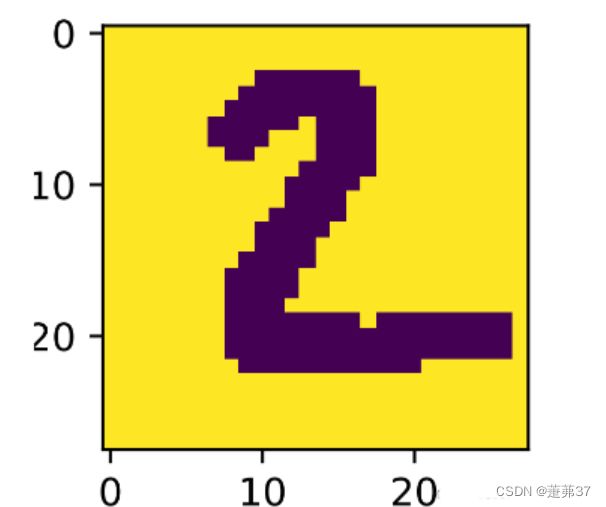
plt.imshow(image)
plt.savefig('cnn-number2.pdf')

运行结果：

The true category is 2 and the predicted category is 2

使用前馈神经网络实现MNIST识别，与LeNet效果对比。（选做）

import numpy as np
import torch
import matplotlib.pyplot as plt
from torchvision.datasets import mnist
from torchvision import transforms
from torch.utils.data import DataLoader
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
 
train_batch_size = 64#超参数
test_batch_size = 128#超参数
learning_rate = 0.01#学习率
nums_epoches = 20#训练次数
lr = 0.1#优化器参数
momentum = 0.5#优化器参数
train_dataset = mnist.MNIST('./data', train=True, transform=transforms.ToTensor(), target_transform=None, download=True)
test_dataset = mnist.MNIST('./data', train=False, transform=transforms.ToTensor(), target_transform=None, download=False)
train_loader = DataLoader(train_dataset, batch_size=train_batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=test_batch_size, shuffle=False)
 
class model(nn.Module):
    def __init__(self, in_dim, hidden_1, hidden_2, out_dim):
        super(model, self).__init__()
        self.layer1 = nn.Sequential(nn.Linear(in_dim, hidden_1, bias=True), nn.BatchNorm1d(hidden_1))
        self.layer2 = nn.Sequential(nn.Linear(hidden_1, hidden_2, bias=True), nn.BatchNorm1d(hidden_2))
        self.layer3 = nn.Sequential(nn.Linear(hidden_2, out_dim))
 
    def forward(self, x):
        # 注意 F 与 nn 下的激活函数使用起来不一样的
        x = F.relu(self.layer1(x))
        x = F.relu(self.layer2(x))
        x = self.layer3(x)
        return x
 
#实例化网络
model = model(28*28,300,100,10)
#定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
#momentum:动量因子
optimizer = optim.SGD(model.parameters(),lr=lr,momentum=momentum)
def train():
    # 开始训练 先定义存储损失函数和准确率的数组
    losses = []
    acces = []
    # 测试用
    eval_losses = []
    eval_acces = []
 
    for epoch in range(nums_epoches):
        # 每次训练先清零
        train_loss = 0
        train_acc = 0
        # 将模型设置为训练模式
        model.train()
        # 动态学习率
        if epoch % 5 == 0:
            optimizer.param_groups[0]['lr'] *= 0.1
        for img, label in train_loader:
            # 例如 img=[64,1,28,28] 做完view()后变为[64,1*28*28]=[64,784]
            # 把图片数据格式转换成与网络匹配的格式
            img = img.view(img.size(0), -1)
            # 前向传播，将图片数据传入模型中
            # out输出10维，分别是各数字的概率，即每个类别的得分
            out = model(img)
            # 这里注意参数out是64*10，label是一维的64
            loss = criterion(out, label)
            # 反向传播
            # optimizer.zero_grad()意思是把梯度置零，也就是把loss关于weight的导数变成0
            optimizer.zero_grad()
            loss.backward()
            # 这个方法会更新所有的参数，一旦梯度被如backward()之类的函数计算好后，我们就可以调用这个函数
            optimizer.step()
            # 记录误差
            train_loss += loss.item()
            # 计算分类的准确率,找到概率最大的下标
            _, pred = out.max(1)
            num_correct = (pred == label).sum().item()  # 记录标签正确的个数
            acc = num_correct / img.shape[0]
            train_acc += acc
        losses.append(train_loss / len(train_loader))
        acces.append(train_acc / len(train_loader))
 
        eval_loss = 0
        eval_acc = 0
        model.eval()
        for img, label in test_loader:
            img = img.view(img.size(0), -1)
 
            out = model(img)
            loss = criterion(out, label)
 
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
 
            eval_loss += loss.item()
 
            _, pred = out.max(1)
            num_correct = (pred == label).sum().item()
            acc = num_correct / img.shape[0]
            eval_acc += acc
        eval_losses.append(eval_loss / len(test_loader))
        eval_acces.append(eval_acc / len(test_loader))
 
        print('epoch:{},Train Loss:{:.4f},Train Acc:{:.4f},Test Loss:{:.4f},Test Acc:{:.4f}'
              .format(epoch, train_loss / len(train_loader), train_acc / len(train_loader),
                      eval_loss / len(test_loader), eval_acc / len(test_loader)))
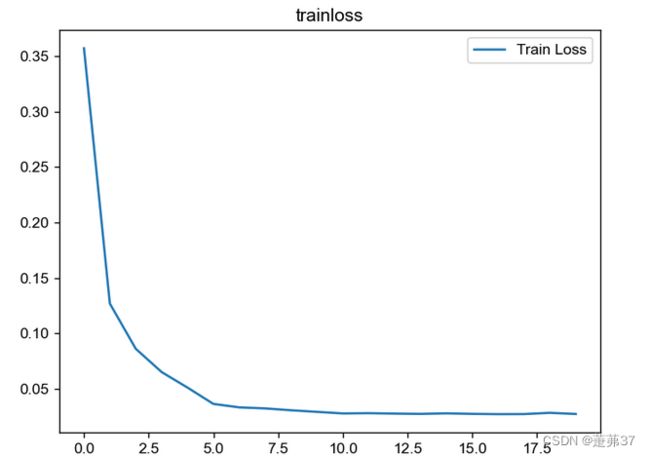
    plt.title('trainloss')
    plt.plot(np.arange(len(losses)), losses)
    plt.legend(['Train Loss'], loc='upper right')
#测试
from sklearn.metrics import confusion_matrix
import seaborn as sns
def test():
    correct = 0
    total = 0
    y_predict=[]
    y_true=[]
    with torch.no_grad():
        for data in test_loader:
            input, target = data
            input = input.view(input.size(0), -1)
            output = model(input)#输出十个最大值
            _, predict = torch.max(output.data, dim=1)#元组取最大值的下表
            #
            #print('predict:',predict)
            total += target.size(0)
            correct += (predict == target).sum().item()
            y_predict.extend(predict.tolist())
            y_true.extend(target.tolist())
    print('正确率：', correct / total)
    print('correct=', correct)
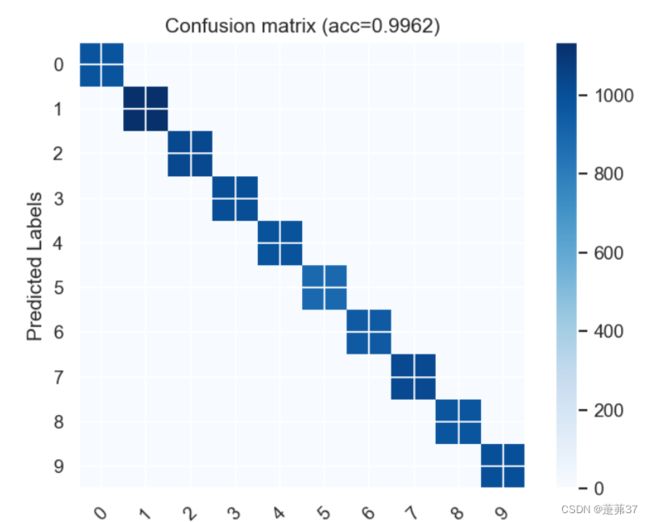
    sns.set()
    f, ax = plt.subplots()
    C2 = confusion_matrix(y_true, y_predict, labels=[0, 1, 2,3,4,5,6,7,8,9])
    print(C2)
    plt.imshow(C2, cmap=plt.cm.Blues)
    plt.xticks(range(10),labels=[0, 1, 2,3,4,5,6,7,8,9] , rotation=45)
    plt.yticks(range(10),labels=[0, 1, 2,3,4,5,6,7,8,9])
    plt.colorbar()
    plt.xlabel('True Labels')
    plt.ylabel('Predicted Labels')
    plt.title('Confusion matrix (acc=' + str(correct / total)+ ')')
 
    plt.show()
 
train()
test()

运行结果：

epoch:0,Train Loss:0.3498,Train Acc:0.9175,Test Loss:0.1283,Test Acc:0.9615
epoch:1,Train Loss:0.1283,Train Acc:0.9650,Test Loss:0.0824,Test Acc:0.9764
epoch:2,Train Loss:0.0881,Train Acc:0.9752,Test Loss:0.0628,Test Acc:0.9827
epoch:3,Train Loss:0.0665,Train Acc:0.9818,Test Loss:0.0503,Test Acc:0.9858
epoch:4,Train Loss:0.0535,Train Acc:0.9854,Test Loss:0.0416,Test Acc:0.9890
epoch:5,Train Loss:0.0368,Train Acc:0.9914,Test Loss:0.0259,Test Acc:0.9948
epoch:6,Train Loss:0.0338,Train Acc:0.9921,Test Loss:0.0255,Test Acc:0.9953
epoch:7,Train Loss:0.0321,Train Acc:0.9934,Test Loss:0.0250,Test Acc:0.9948
epoch:8,Train Loss:0.0307,Train Acc:0.9931,Test Loss:0.0245,Test Acc:0.9955
epoch:9,Train Loss:0.0299,Train Acc:0.9937,Test Loss:0.0240,Test Acc:0.9955
epoch:10,Train Loss:0.0280,Train Acc:0.9943,Test Loss:0.0239,Test Acc:0.9955
epoch:11,Train Loss:0.0289,Train Acc:0.9940,Test Loss:0.0241,Test Acc:0.9955
epoch:12,Train Loss:0.0282,Train Acc:0.9943,Test Loss:0.0235,Test Acc:0.9963
epoch:13,Train Loss:0.0278,Train Acc:0.9947,Test Loss:0.0237,Test Acc:0.9963
epoch:14,Train Loss:0.0279,Train Acc:0.9944,Test Loss:0.0235,Test Acc:0.9960
epoch:15,Train Loss:0.0276,Train Acc:0.9945,Test Loss:0.0233,Test Acc:0.9957
epoch:16,Train Loss:0.0268,Train Acc:0.9948,Test Loss:0.0238,Test Acc:0.9962
epoch:17,Train Loss:0.0270,Train Acc:0.9950,Test Loss:0.0240,Test Acc:0.9960
epoch:18,Train Loss:0.0277,Train Acc:0.9947,Test Loss:0.0233,Test Acc:0.9960
epoch:19,Train Loss:0.0271,Train Acc:0.9946,Test Loss:0.0238,Test Acc:0.9959
正确率： 0.9959
correct= 9959
[[ 979    0    0    0    0    0    0    1    0    0]
 [   0 1132    0    0    0    0    2    0    1    0]
 [   0    0 1030    0    0    0    0    2    0    0]
 [   0    0    0 1008    0    1    0    1    0    0]
 [   0    0    1    0  979    0    1    0    0    1]
 [   2    0    0    0    0  888    1    0    0    1]
 [   3    2    0    0    1    2  950    0    0    0]
 [   0    3    1    1    0    0    0 1021    0    2]
 [   0    0    0    2    0    0    0    0  972    0]
 [   2    1    0    1    2    1    0    2    0 1000]]
 
进程已结束，退出代码为 0

通过time函数发现卷积神经网络会快很多，并且需要的轮数也会较多，需要的数据上也是较多的，所以直接即可提现出卷积神经网络的优越性。

可视化LeNet中的部分特征图和卷积核，谈谈自己的看法。（选做）

class Paddle_LeNet1(nn.Module):
    def __init__(self, in_channels, num_classes=10):
        super(Paddle_LeNet1, self).__init__()
        # 卷积层：输出通道数为6，卷积核大小为5*5
        self.conv1 = nn.Conv2d(in_channels=in_channels, out_channels=6, kernel_size=5)
        # 汇聚层：汇聚窗口为2*2，步长为2
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        # 卷积层：输入通道数为6，输出通道数为16，卷积核大小为5*5
        self.conv3 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
        # 汇聚层：汇聚窗口为2*2，步长为2
        self.pool4 = nn.AvgPool2d(kernel_size=2, stride=2)
        # 卷积层：输入通道数为16，输出通道数为120，卷积核大小为5*5
        self.conv5 = nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5)
        # 全连接层：输入神经元为120，输出神经元为84
        self.linear6 = nn.Linear(in_features=120, out_features=84)
        # 全连接层：输入神经元为84，输出神经元为类别数
        self.linear7 = nn.Linear(in_features=84, out_features=num_classes)
 
    def forward(self, x):
        image=[]
        # C1：卷积层+激活函数
        output = F.relu(self.conv1(x))
        image.append(output)
        # S2：汇聚层
        output = self.pool2(output)
 
        # C3：卷积层+激活函数
        output = F.relu(self.conv3(output))
        image.append(output)
        # S4：汇聚层
        output = self.pool4(output)
        # C5：卷积层+激活函数
        output = F.relu(self.conv5(output))
        image.append(output)
        # 输入层将数据拉平[B,C,H,W] -> [B,CxHxW]
        output = torch.squeeze(output, dim=3)
        output = torch.squeeze(output, dim=2)
        # F6：全连接层
        output = F.relu(self.linear6(output))
        # F7：全连接层
        output = self.linear7(output)
        return image 
# create model
model1 = Paddle_LeNet1(in_channels=1, num_classes=10)
 
 
# model_weight_path ="./AlexNet.pth"
model_weight_path = 'best_model.pdparams'
model1.load_state_dict(torch.load(model_weight_path))
 
 
# forward正向传播过程
out_put = model1(X)
print(out_put[0].shape)
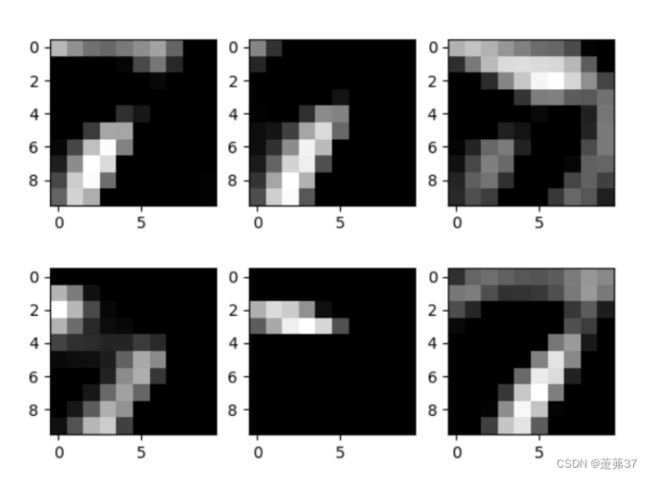
for i in range(0,3):
 for feature_map in out_put[i]:
    # [N, C, H, W] -> [C, H, W]    维度变换
    im = np.squeeze(feature_map.detach().numpy())
    # [C, H, W] -> [H, W, C]
    im = np.transpose(im, [1, 2, 0])
    print(im.shape)
 
    # show 9 feature maps
    plt.figure()
    for i in range(6):
        ax = plt.subplot(2, 3, i + 1)  # 参数意义：3：图片绘制行数，5：绘制图片列数，i+1：图的索引
        # [H, W, C]
        # 特征矩阵每一个channel对应的是一个二维的特征矩阵，就像灰度图像一样，channel=1
        # plt.imshow(im[:, :, i])i,,
        plt.imshow(im[:, :, i], cmap='gray')
    plt.show()
    break

运行结果：

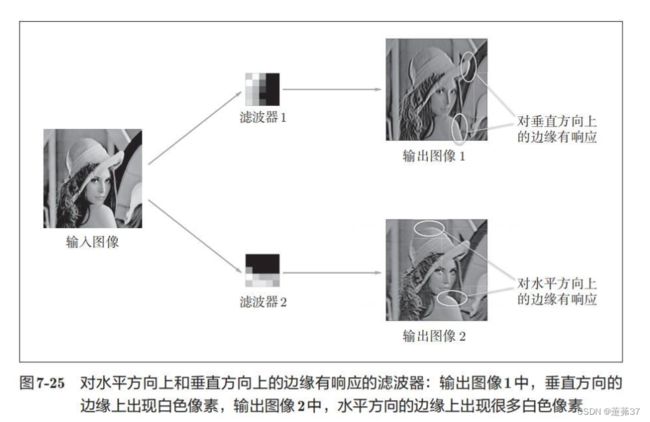
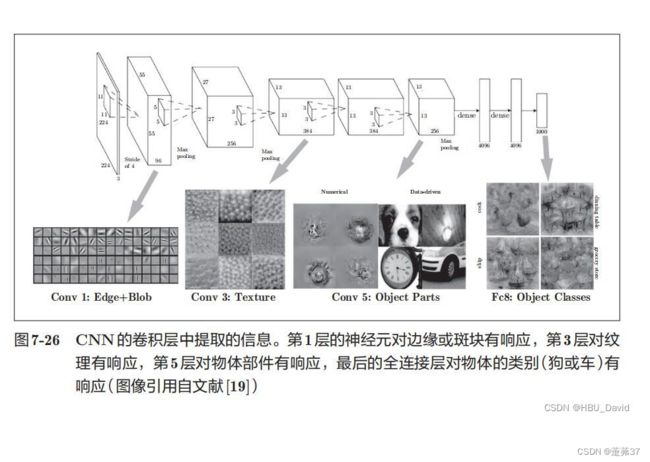
通过可视化部分特征图和卷积核，让我认识到特征是经过一步步慢慢提取出来的，后经过池化和全连接等等，才形成了一个较为完整的特征。也就是中间的卷积核是特征中点、线、边的组合，即组合出一些小的特征，但是最后的卷积核就会是这些小的多特征的组合。

总结

通过本次实验对LeNet网络的构建和参数量、计算量有了更深的了解，通过使用前馈神经网络识别MNIST数据集与LeNet网络进行对比对训练效果有了更直观的掌握。直观的可视化了一下部分特征图和卷积核，对特征提取的过程理解更深了，同时也体会到了卷积神经网络的优越性。了解了前馈神经网络和卷积神经网络都有较好的准确率。

参考

NNDL 实验5（上） - HBU_DAVID - 博客园 (cnblogs.com)
NNDL 实验5（下） - HBU_DAVID - 博客园 (cnblogs.com)
6. 卷积神经网络 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)
7. 现代卷积神经网络 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)
详解深度学习之经典网络架构（一）：LeNet