NNDL 实验六 卷积神经网络(4)ResNet18实现MNIST
文章目录
-
- 5.4 基于残差网络的手写体数字识别实验
-
- 5.4.1 模型构建
-
- 5.4.1.1 残差单元
- 5.4.1.2 残差网络的整体结构
- 5.4.2 没有残差连接的ResNet18
-
- 5.4.2.1 模型训练
- 5.4.2.2 模型评价
- 5.4.3 带残差连接的ResNet18
-
- 5.4.3.1 模型训练
- 5.4.3.2 模型评价
- 5.4.4 与高层API实现版本的对比实验
- 学习并在实验中使用:Pytorch torchvision.models
- 总结
- 参考
5.4 基于残差网络的手写体数字识别实验
残差网络(Residual Network,ResNet)是在神经网络模型中给非线性层增加直连边的方式来缓解梯度消失问题,从而使训练深度神经网络变得更加容易。
 在残差网络中,最基本的单位为残差单元。
在残差网络中,最基本的单位为残差单元。

5.4.1 模型构建
构建ResNet18的残差单元,然后在组建完整的网络。
5.4.1.1 残差单元
这里,我们实现一个算子ResBlock来构建残差单元,其中定义了use_residual参数,用于在后续实验中控制是否使用残差连接。
残差单元包裹的非线性层的输入和输出形状大小应该一致。如果一个卷积层的输入特征图和输出特征图的通道数不一致,则其输出与输入特征图无法直接相加。为了解决上述问题,可以使用1×1大小的卷积将输入特征图的通道数映射为与级联卷积输出特征图的一致通道数。
1×1卷积:与标准卷积完全一样,唯一的特殊点在于卷积核的尺寸是1×1,也就是不去考虑输入数据局部信息之间的关系,而把关注点放在不同通道间。通过使用1×1卷积,可以起到如下作用:
- 实现信息的跨通道交互与整合。考虑到卷积运算的输入输出都是3个维度(宽、高、多通道),所以1×1卷积实际上就是对每个像素点,在不同的通道上进行线性组合,从而整合不同通道的信息;
- 对卷积核通道数进行降维和升维,减少参数量。经过1×1卷积后的输出保留了输入数据的原有平面结构,通过调控通道数,从而完成升维或降维的作用;
- 利用1×1卷积后的非线性激活函数,在保持特征图尺寸不变的前提下,大幅增加非线性。
class ResBlock(nn.Module):
def __init__(self, in_channels, out_channels, stride=1, use_residual=True):
super(ResBlock, self).__init__()
self.stride = stride
self.use_residual = use_residual
# 第一个卷积层,卷积核大小为3×3,可以设置不同输出通道数以及步长
self.conv1 = nn.Conv2d(in_channels, out_channels, 3, padding=1, stride=self.stride, bias=False)
# 第二个卷积层,卷积核大小为3×3,不改变输入特征图的形状,步长为1
self.conv2 = nn.Conv2d(out_channels, out_channels, 3, padding=1, bias=False)
# 如果conv2的输出和此残差块的输入数据形状不一致,则use_1x1conv = True
# 当use_1x1conv = True,添加1个1x1的卷积作用在输入数据上,使其形状变成跟conv2一致
if in_channels != out_channels or stride != 1:
self.use_1x1conv = True
else:
self.use_1x1conv = False
# 当残差单元包裹的非线性层输入和输出通道数不一致时,需要用1×1卷积调整通道数后再进行相加运算
if self.use_1x1conv:
self.shortcut = nn.Conv2d(in_channels, out_channels, 1, stride=self.stride, bias=False)
# 每个卷积层后会接一个批量规范化层,批量规范化的内容在7.5.1中会进行详细介绍
self.bn1 = nn.BatchNorm2d(out_channels)
self.bn2 = nn.BatchNorm2d(out_channels)
if self.use_1x1conv:
self.bn3 = nn.BatchNorm2d(out_channels)
def forward(self, inputs):
y = F.relu(self.bn1(self.conv1(inputs)))
y = self.bn2(self.conv2(y))
if self.use_residual:
if self.use_1x1conv: # 如果为真,对inputs进行1×1卷积,将形状调整成跟conv2的输出y一致
shortcut = self.shortcut(inputs)
shortcut = self.bn3(shortcut)
else: # 否则直接将inputs和conv2的输出y相加
shortcut = inputs
y = torch.add(shortcut, y)
out = F.relu(y)
return out
5.4.1.2 残差网络的整体结构
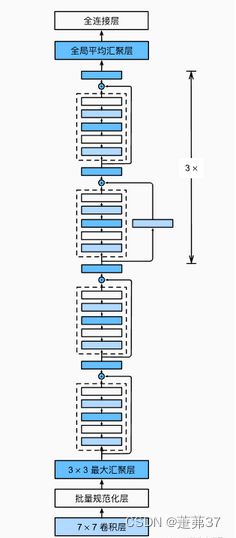
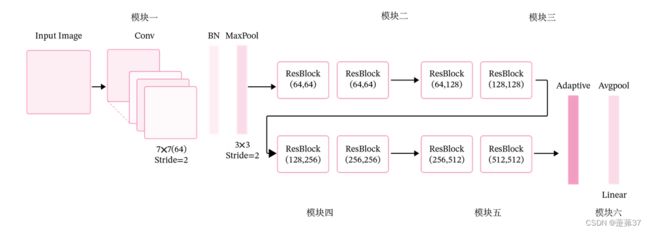
残差网络就是将很多个残差单元串联起来构成的一个非常深的网络。ResNet18 的网络结构如下图所示。
 其中为了便于理解,可以将ResNet18网络划分为6个模块:
其中为了便于理解,可以将ResNet18网络划分为6个模块:
第一模块:包含了一个步长为2,大小为7×7的卷积层,卷积层的输出通道数为64,卷积层的输出经过批量归一化、ReLU激活函数的处理后,接了一个步长为2的3×3的最大汇聚层;
第二模块:包含了两个残差单元,经过运算后,输出通道数为64,特征图的尺寸保持不变;
第三模块:包含了两个残差单元,经过运算后,输出通道数为128,特征图的尺寸缩小一半;
第四模块:包含了两个残差单元,经过运算后,输出通道数为256,特征图的尺寸缩小一半;
第五模块:包含了两个残差单元,经过运算后,输出通道数为512,特征图的尺寸缩小一半;
第六模块:包含了一个全局平均汇聚层,将特征图变为1×1的大小,最终经过全连接层计算出最后的输出。
ResNet18模型的代码实现如下:
定义模块一:
def make_first_module(in_channels):
# 模块一:7*7卷积、批量规范化、汇聚
m1 = nn.Sequential(nn.Conv2d(in_channels, 64, 7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
return m1
定义模块二到模块五:
def resnet_module(input_channels, out_channels, num_res_blocks, stride=1, use_residual=True):
blk = []
# 根据num_res_blocks,循环生成残差单元
for i in range(num_res_blocks):
if i == 0: # 创建模块中的第一个残差单元
blk.append(ResBlock(input_channels, out_channels,
stride=stride, use_residual=use_residual))
else: # 创建模块中的其他残差单元
blk.append(ResBlock(out_channels, out_channels, use_residual=use_residual))
return blk
封装模块二到模块五:
def make_modules(use_residual):
# 模块二:包含两个残差单元,输入通道数为64,输出通道数为64,步长为1,特征图大小保持不变
m2 = nn.Sequential(*resnet_module(64, 64, 2, stride=1, use_residual=use_residual))
# 模块三:包含两个残差单元,输入通道数为64,输出通道数为128,步长为2,特征图大小缩小一半。
m3 = nn.Sequential(*resnet_module(64, 128, 2, stride=2, use_residual=use_residual))
# 模块四:包含两个残差单元,输入通道数为128,输出通道数为256,步长为2,特征图大小缩小一半。
m4 = nn.Sequential(*resnet_module(128, 256, 2, stride=2, use_residual=use_residual))
# 模块五:包含两个残差单元,输入通道数为256,输出通道数为512,步长为2,特征图大小缩小一半。
m5 = nn.Sequential(*resnet_module(256, 512, 2, stride=2, use_residual=use_residual))
return m2, m3, m4, m5
定义完整网络:
# 定义完整网络
class Model_ResNet18(nn.Module):
def __init__(self, in_channels=3, num_classes=10, use_residual=True):
super(Model_ResNet18,self).__init__()
m1 = make_first_module(in_channels)
m2, m3, m4, m5 = make_modules(use_residual)
# 封装模块一到模块6
self.net = nn.Sequential(m1, m2, m3, m4, m5,
# 模块六:汇聚层、全连接层
nn.AdaptiveAvgPool2d(1), nn.Flatten(), nn.Linear(512, num_classes) )
def forward(self, x):
return self.net(x)
使用torchsummary.summary统计模型的参数量。
from torchsummary import summary
model = Model_ResNet18(in_channels=1, num_classes=10, use_residual=True)
params_info = summary(model,input_size=(1,64,32))
print(params_info)
运行结果:
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 64, 16, 16] 3,200
BatchNorm2d-2 [-1, 64, 16, 16] 128
ReLU-3 [-1, 64, 16, 16] 0
MaxPool2d-4 [-1, 64, 8, 8] 0
Conv2d-5 [-1, 64, 8, 8] 36,864
BatchNorm2d-6 [-1, 64, 8, 8] 128
Conv2d-7 [-1, 64, 8, 8] 36,864
BatchNorm2d-8 [-1, 64, 8, 8] 128
ResBlock-9 [-1, 64, 8, 8] 0
Conv2d-10 [-1, 64, 8, 8] 36,864
BatchNorm2d-11 [-1, 64, 8, 8] 128
Conv2d-12 [-1, 64, 8, 8] 36,864
BatchNorm2d-13 [-1, 64, 8, 8] 128
ResBlock-14 [-1, 64, 8, 8] 0
Conv2d-15 [-1, 128, 4, 4] 73,728
BatchNorm2d-16 [-1, 128, 4, 4] 256
Conv2d-17 [-1, 128, 4, 4] 147,456
BatchNorm2d-18 [-1, 128, 4, 4] 256
Conv2d-19 [-1, 128, 4, 4] 8,192
BatchNorm2d-20 [-1, 128, 4, 4] 256
ResBlock-21 [-1, 128, 4, 4] 0
Conv2d-22 [-1, 128, 4, 4] 147,456
BatchNorm2d-23 [-1, 128, 4, 4] 256
Conv2d-24 [-1, 128, 4, 4] 147,456
BatchNorm2d-25 [-1, 128, 4, 4] 256
ResBlock-26 [-1, 128, 4, 4] 0
Conv2d-27 [-1, 256, 2, 2] 294,912
BatchNorm2d-28 [-1, 256, 2, 2] 512
Conv2d-29 [-1, 256, 2, 2] 589,824
BatchNorm2d-30 [-1, 256, 2, 2] 512
Conv2d-31 [-1, 256, 2, 2] 32,768
BatchNorm2d-32 [-1, 256, 2, 2] 512
ResBlock-33 [-1, 256, 2, 2] 0
Conv2d-34 [-1, 256, 2, 2] 589,824
BatchNorm2d-35 [-1, 256, 2, 2] 512
Conv2d-36 [-1, 256, 2, 2] 589,824
BatchNorm2d-37 [-1, 256, 2, 2] 512
ResBlock-38 [-1, 256, 2, 2] 0
Conv2d-39 [-1, 512, 1, 1] 1,179,648
BatchNorm2d-40 [-1, 512, 1, 1] 1,024
Conv2d-41 [-1, 512, 1, 1] 2,359,296
BatchNorm2d-42 [-1, 512, 1, 1] 1,024
Conv2d-43 [-1, 512, 1, 1] 131,072
BatchNorm2d-44 [-1, 512, 1, 1] 1,024
ResBlock-45 [-1, 512, 1, 1] 0
Conv2d-46 [-1, 512, 1, 1] 2,359,296
BatchNorm2d-47 [-1, 512, 1, 1] 1,024
Conv2d-48 [-1, 512, 1, 1] 2,359,296
BatchNorm2d-49 [-1, 512, 1, 1] 1,024
ResBlock-50 [-1, 512, 1, 1] 0
AdaptiveAvgPool2d-51 [-1, 512, 1, 1] 0
Flatten-52 [-1, 512] 0
Linear-53 [-1, 10] 5,130
================================================================
Total params: 11,175,434
Trainable params: 11,175,434
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 1.05
Params size (MB): 42.63
Estimated Total Size (MB): 43.69
----------------------------------------------------------------
使用torchstat统计模型的计算量。
from torchstat import stat
model = Model_ResNet18(in_channels=1, num_classes=10, use_residual=True)
stat(model, (1, 32, 32))
运行结果:
[MAdd]: AdaptiveAvgPool2d is not supported!
[Flops]: AdaptiveAvgPool2d is not supported!
[Memory]: AdaptiveAvgPool2d is not supported!
[MAdd]: Flatten is not supported!
[Flops]: Flatten is not supported!
[Memory]: Flatten is not supported!
df = df.append(total_df)
module name input shape output shape params memory(MB) MAdd Flops MemRead(B) MemWrite(B) duration[%] MemR+W(B)
0 net.0.0 1 32 32 64 16 16 3200.0 0.06 1,605,632.0 819,200.0 16896.0 65536.0 11.11% 82432.0
1 net.0.1 64 16 16 64 16 16 128.0 0.06 65,536.0 32,768.0 66048.0 65536.0 11.11% 131584.0
2 net.0.2 64 16 16 64 16 16 0.0 0.06 16,384.0 16,384.0 65536.0 65536.0 0.00% 131072.0
3 net.0.3 64 16 16 64 8 8 0.0 0.02 32,768.0 16,384.0 65536.0 16384.0 0.00% 81920.0
4 net.1.0.conv1 64 8 8 64 8 8 36864.0 0.02 4,714,496.0 2,359,296.0 163840.0 16384.0 11.11% 180224.0
5 net.1.0.conv2 64 8 8 64 8 8 36864.0 0.02 4,714,496.0 2,359,296.0 163840.0 16384.0 0.00% 180224.0
6 net.1.0.bn1 64 8 8 64 8 8 128.0 0.02 16,384.0 8,192.0 16896.0 16384.0 0.00% 33280.0
7 net.1.0.bn2 64 8 8 64 8 8 128.0 0.02 16,384.0 8,192.0 16896.0 16384.0 0.00% 33280.0
8 net.1.1.conv1 64 8 8 64 8 8 36864.0 0.02 4,714,496.0 2,359,296.0 163840.0 16384.0 11.11% 180224.0
9 net.1.1.conv2 64 8 8 64 8 8 36864.0 0.02 4,714,496.0 2,359,296.0 163840.0 16384.0 0.00% 180224.0
10 net.1.1.bn1 64 8 8 64 8 8 128.0 0.02 16,384.0 8,192.0 16896.0 16384.0 0.00% 33280.0
11 net.1.1.bn2 64 8 8 64 8 8 128.0 0.02 16,384.0 8,192.0 16896.0 16384.0 0.00% 33280.0
12 net.2.0.conv1 64 8 8 128 4 4 73728.0 0.01 2,357,248.0 1,179,648.0 311296.0 8192.0 0.00% 319488.0
13 net.2.0.conv2 128 4 4 128 4 4 147456.0 0.01 4,716,544.0 2,359,296.0 598016.0 8192.0 0.00% 606208.0
14 net.2.0.shortcut 64 8 8 128 4 4 8192.0 0.01 260,096.0 131,072.0 49152.0 8192.0 0.00% 57344.0
15 net.2.0.bn1 128 4 4 128 4 4 256.0 0.01 8,192.0 4,096.0 9216.0 8192.0 11.11% 17408.0
16 net.2.0.bn2 128 4 4 128 4 4 256.0 0.01 8,192.0 4,096.0 9216.0 8192.0 0.00% 17408.0
17 net.2.0.bn3 128 4 4 128 4 4 256.0 0.01 8,192.0 4,096.0 9216.0 8192.0 0.00% 17408.0
18 net.2.1.conv1 128 4 4 128 4 4 147456.0 0.01 4,716,544.0 2,359,296.0 598016.0 8192.0 11.11% 606208.0
19 net.2.1.conv2 128 4 4 128 4 4 147456.0 0.01 4,716,544.0 2,359,296.0 598016.0 8192.0 0.00% 606208.0
20 net.2.1.bn1 128 4 4 128 4 4 256.0 0.01 8,192.0 4,096.0 9216.0 8192.0 0.00% 17408.0
21 net.2.1.bn2 128 4 4 128 4 4 256.0 0.01 8,192.0 4,096.0 9216.0 8192.0 0.00% 17408.0
22 net.3.0.conv1 128 4 4 256 2 2 294912.0 0.00 2,358,272.0 1,179,648.0 1187840.0 4096.0 0.00% 1191936.0
23 net.3.0.conv2 256 2 2 256 2 2 589824.0 0.00 4,717,568.0 2,359,296.0 2363392.0 4096.0 0.00% 2367488.0
24 net.3.0.shortcut 128 4 4 256 2 2 32768.0 0.00 261,120.0 131,072.0 139264.0 4096.0 0.00% 143360.0
25 net.3.0.bn1 256 2 2 256 2 2 512.0 0.00 4,096.0 2,048.0 6144.0 4096.0 0.00% 10240.0
26 net.3.0.bn2 256 2 2 256 2 2 512.0 0.00 4,096.0 2,048.0 6144.0 4096.0 0.00% 10240.0
27 net.3.0.bn3 256 2 2 256 2 2 512.0 0.00 4,096.0 2,048.0 6144.0 4096.0 0.00% 10240.0
28 net.3.1.conv1 256 2 2 256 2 2 589824.0 0.00 4,717,568.0 2,359,296.0 2363392.0 4096.0 0.00% 2367488.0
29 net.3.1.conv2 256 2 2 256 2 2 589824.0 0.00 4,717,568.0 2,359,296.0 2363392.0 4096.0 11.11% 2367488.0
30 net.3.1.bn1 256 2 2 256 2 2 512.0 0.00 4,096.0 2,048.0 6144.0 4096.0 0.00% 10240.0
31 net.3.1.bn2 256 2 2 256 2 2 512.0 0.00 4,096.0 2,048.0 6144.0 4096.0 0.00% 10240.0
32 net.4.0.conv1 256 2 2 512 1 1 1179648.0 0.00 2,358,784.0 1,179,648.0 4722688.0 2048.0 11.11% 4724736.0
33 net.4.0.conv2 512 1 1 512 1 1 2359296.0 0.00 4,718,080.0 2,359,296.0 9439232.0 2048.0 0.00% 9441280.0
34 net.4.0.shortcut 256 2 2 512 1 1 131072.0 0.00 261,632.0 131,072.0 528384.0 2048.0 0.00% 530432.0
35 net.4.0.bn1 512 1 1 512 1 1 1024.0 0.00 2,048.0 1,024.0 6144.0 2048.0 0.00% 8192.0
36 net.4.0.bn2 512 1 1 512 1 1 1024.0 0.00 2,048.0 1,024.0 6144.0 2048.0 0.00% 8192.0
37 net.4.0.bn3 512 1 1 512 1 1 1024.0 0.00 2,048.0 1,024.0 6144.0 2048.0 0.00% 8192.0
38 net.4.1.conv1 512 1 1 512 1 1 2359296.0 0.00 4,718,080.0 2,359,296.0 9439232.0 2048.0 0.00% 9441280.0
39 net.4.1.conv2 512 1 1 512 1 1 2359296.0 0.00 4,718,080.0 2,359,296.0 9439232.0 2048.0 0.00% 9441280.0
40 net.4.1.bn1 512 1 1 512 1 1 1024.0 0.00 2,048.0 1,024.0 6144.0 2048.0 0.00% 8192.0
41 net.4.1.bn2 512 1 1 512 1 1 1024.0 0.00 2,048.0 1,024.0 6144.0 2048.0 0.00% 8192.0
42 net.5 512 1 1 512 1 1 0.0 0.00 0.0 0.0 0.0 0.0 11.11% 0.0
43 net.6 512 1 1 512 0.0 0.00 0.0 0.0 0.0 0.0 0.00% 0.0
44 net.7 512 10 5130.0 0.00 10,230.0 5,120.0 22568.0 40.0 0.00% 22608.0
total 11175434.0 0.47 71,039,478.0 35,561,472.0 22568.0 40.0 100.00% 45695056.0
=====================================================================================================================================================
Total params: 11,175,434
-----------------------------------------------------------------------------------------------------------------------------------------------------
Total memory: 0.47MB
Total MAdd: 71.04MMAdd
Total Flops: 35.56MFlops
Total MemR+W: 43.58MB
进程已结束,退出代码为 0
为了验证残差连接对深层卷积神经网络的训练可以起到促进作用,接下来先使用ResNet18(use_residual设置为False)进行手写数字识别实验,再添加残差连接(use_residual设置为True),观察实验对比效果。
5.4.2 没有残差连接的ResNet18
为了验证残差连接的效果,先使用没有残差连接的ResNet18进行实验。
5.4.2.1 模型训练
使用训练集和验证集进行模型训练,共训练5个epoch。在实验中,保存准确率最高的模型作为最佳模型。代码如下:
torch.manual_seed(100)
# 学习率大小
lr = 0.005
# 批次大小
batch_size = 64
# 加载数据
train_loader = data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = data.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = data.DataLoader(test_dataset, batch_size=batch_size)
# 定义网络,不使用残差结构的深层网络
model = Model_ResNet18(in_channels=1, num_classes=10, use_residual=False)
# 定义优化器
optimizer = opt.SGD(lr=lr, params=model.parameters())
# 定义损失函数
loss_fn = F.cross_entropy
# 定义评价指标
metric = metric.Accuracy(is_logist=True)
# 实例化RunnerV3
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 启动训练
log_steps = 15
eval_steps = 15
runner.train(train_loader, dev_loader, num_epochs=5, log_steps=log_steps,
eval_steps=eval_steps, save_path="best_model.pdparams")
# 可视化观察训练集与验证集的Loss变化情况
plot(runner, 'cnn-loss2.pdf')
plot:
# 可视化
def plot(runner, fig_name):
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
train_items = runner.train_step_losses[::30]
train_steps = [x[0] for x in train_items]
train_losses = [x[1] for x in train_items]
plt.plot(train_steps, train_losses, color='#8E004D', label="Train loss")
if runner.dev_losses[0][0] != -1:
dev_steps = [x[0] for x in runner.dev_losses]
dev_losses = [x[1] for x in runner.dev_losses]
plt.plot(dev_steps, dev_losses, color='#E20079', linestyle='--', label="Dev loss")
# 绘制坐标轴和图例
plt.ylabel("loss", fontsize='x-large')
plt.xlabel("step", fontsize='x-large')
plt.legend(loc='upper right', fontsize='x-large')
plt.subplot(1, 2, 2)
# 绘制评价准确率变化曲线
if runner.dev_losses[0][0] != -1:
plt.plot(dev_steps, runner.dev_scores,
color='#E20079', linestyle="--", label="Dev accuracy")
else:
plt.plot(list(range(len(runner.dev_scores))), runner.dev_scores,
color='#E20079', linestyle="--", label="Dev accuracy")
# 绘制坐标轴和图例
plt.ylabel("score", fontsize='x-large')
plt.xlabel("step", fontsize='x-large')
plt.legend(loc='lower right', fontsize='x-large')
plt.savefig(fig_name)
plt.show()
Accuracy:
class Accuracy():
def __init__(self, is_logist=True):
# 用于统计正确的样本个数
self.num_correct = 0
# 用于统计样本的总数
self.num_count = 0
self.is_logist = is_logist
def update(self, outputs, labels):
# 判断是二分类任务还是多分类任务,shape[1]=1时为二分类任务,shape[1]>1时为多分类任务
if outputs.shape[1] == 1: # 二分类
outputs = torch.squeeze(outputs, dim=-1)
if self.is_logist:
# logist判断是否大于0
preds = torch.tensor((outputs >= 0), dtype=torch.float32)
else:
# 如果不是logist,判断每个概率值是否大于0.5,当大于0.5时,类别为1,否则类别为0
preds = torch.tensor((outputs >= 0.5), dtype=torch.float32)
else:
# 多分类时,使用'torch.argmax'计算最大元素索引作为类别
preds = torch.argmax(outputs, dim=1)
# 获取本批数据中预测正确的样本个数
labels = torch.squeeze(labels, dim=-1)
batch_correct = torch.sum(torch.tensor(preds == labels, dtype=torch.float32)).numpy()
batch_count = len(labels)
# 更新num_correct 和 num_count
self.num_correct += batch_correct
self.num_count += batch_count
def accumulate(self):
# 使用累计的数据,计算总的指标
if self.num_count == 0:
return 0
return self.num_correct / self.num_count
def reset(self):
# 重置正确的数目和总数
self.num_correct = 0
self.num_count = 0
def name(self):
return "Accuracy"
RunnerV3:
class RunnerV3(object):
def __init__(self, model, optimizer, loss_fn, metric, **kwargs):
self.model = model
self.optimizer = optimizer
self.loss_fn = loss_fn
self.metric = metric # 只用于计算评价指标
# 记录训练过程中的评价指标变化情况
self.dev_scores = []
# 记录训练过程中的损失函数变化情况
self.train_epoch_losses = [] # 一个epoch记录一次loss
self.train_step_losses = [] # 一个step记录一次loss
self.dev_losses = []
# 记录全局最优指标
self.best_score = 0
def train(self, train_loader, dev_loader=None, **kwargs):
# 将模型切换为训练模式
self.model.train()
# 传入训练轮数,如果没有传入值则默认为0
num_epochs = kwargs.get("num_epochs", 0)
# 传入log打印频率,如果没有传入值则默认为100
log_steps = kwargs.get("log_steps", 100)
# 评价频率
eval_steps = kwargs.get("eval_steps", 0)
# 传入模型保存路径,如果没有传入值则默认为"best_model.pdparams"
save_path = kwargs.get("save_path", "best_model.pdparams")
custom_print_log = kwargs.get("custom_print_log", None)
# 训练总的步数
num_training_steps = num_epochs * len(train_loader)
if eval_steps:
if self.metric is None:
raise RuntimeError('Error: Metric can not be None!')
if dev_loader is None:
raise RuntimeError('Error: dev_loader can not be None!')
# 运行的step数目
global_step = 0
# 进行num_epochs轮训练
for epoch in range(num_epochs):
# 用于统计训练集的损失
total_loss = 0
for step, data in enumerate(train_loader):
X, y = data
# 获取模型预测
logits = self.model(X)
loss = self.loss_fn(logits, y) # 默认求mean
total_loss += loss
# 训练过程中,每个step的loss进行保存
self.train_step_losses.append((global_step, loss.item()))
if log_steps and global_step % log_steps == 0:
print(
f"[Train] epoch: {epoch}/{num_epochs}, step: {global_step}/{num_training_steps}, loss: {loss.item():.5f}")
# 梯度反向传播,计算每个参数的梯度值
loss.backward()
if custom_print_log:
custom_print_log(self)
# 小批量梯度下降进行参数更新
self.optimizer.step()
# 梯度归零
self.optimizer.zero_grad()
# 判断是否需要评价
if eval_steps > 0 and global_step > 0 and \
(global_step % eval_steps == 0 or global_step == (num_training_steps - 1)):
dev_score, dev_loss = self.evaluate(dev_loader, global_step=global_step)
print(f"[Evaluate] dev score: {dev_score:.5f}, dev loss: {dev_loss:.5f}")
# 将模型切换为训练模式
self.model.train()
# 如果当前指标为最优指标,保存该模型
if dev_score > self.best_score:
self.save_model(save_path)
print(
f"[Evaluate] best accuracy performence has been updated: {self.best_score:.5f} --> {dev_score:.5f}")
self.best_score = dev_score
global_step += 1
# 当前epoch 训练loss累计值
trn_loss = (total_loss / len(train_loader)).item()
# epoch粒度的训练loss保存
self.train_epoch_losses.append(trn_loss)
print("[Train] Training done!")
# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度
@torch.no_grad()
def evaluate(self, dev_loader, **kwargs):
assert self.metric is not None
# 将模型设置为评估模式
self.model.eval()
global_step = kwargs.get("global_step", -1)
# 用于统计训练集的损失
total_loss = 0
# 重置评价
self.metric.reset()
# 遍历验证集每个批次
for batch_id, data in enumerate(dev_loader):
X, y = data
# 计算模型输出
logits = self.model(X)
# 计算损失函数
loss = self.loss_fn(logits, y).item()
# 累积损失
total_loss += loss
# 累积评价
self.metric.update(logits, y)
dev_loss = (total_loss / len(dev_loader))
dev_score = self.metric.accumulate()
# 记录验证集loss
if global_step != -1:
self.dev_losses.append((global_step, dev_loss))
self.dev_scores.append(dev_score)
return dev_score, dev_loss
# 模型评估阶段,使用'paddle.no_grad()'控制不计算和存储梯度
@torch.no_grad()
def predict(self, x, **kwargs):
# 将模型设置为评估模式
self.model.eval()
# 运行模型前向计算,得到预测值
logits = self.model(x)
return logits
def save_model(self, save_path):
torch.save(self.model.state_dict(), save_path)
def load_model(self, model_path):
state_dict = torch.load(model_path)
self.model.load_state_dict(state_dict)
运行结果:
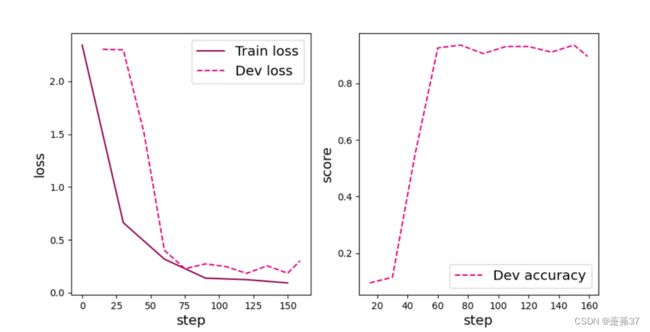
[Train] epoch: 0/5, step: 0/80, loss: 2.31209
[Train] epoch: 0/5, step: 15/80, loss: 0.86413
[Evaluate] dev score: 0.11000, dev loss: 2.30072
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.11000
[Train] epoch: 1/5, step: 30/80, loss: 0.45704
[Evaluate] dev score: 0.11000, dev loss: 2.29350
[Train] epoch: 2/5, step: 45/80, loss: 0.18045
[Evaluate] dev score: 0.72000, dev loss: 1.29890
[Evaluate] best accuracy performence has been updated: 0.11000 --> 0.72000
[Train] epoch: 3/5, step: 60/80, loss: 0.08861
[Evaluate] dev score: 0.91000, dev loss: 0.41233
[Evaluate] best accuracy performence has been updated: 0.72000 --> 0.91000
[Train] epoch: 4/5, step: 75/80, loss: 0.07691
[Evaluate] dev score: 0.93500, dev loss: 0.29393
[Evaluate] best accuracy performence has been updated: 0.91000 --> 0.93500
[Evaluate] dev score: 0.92500, dev loss: 0.24343
[Train] Training done!
5.4.2.2 模型评价
使用测试数据对在训练过程中保存的最佳模型进行评价,观察模型在测试集上的准确率以及损失情况。代码如下:
# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))
运行结果:
[Test] accuracy/loss: 0.9500/0.2424
从输出结果看,对比LeNet-5模型评价实验结果,网络层级加深后,训练效果不升反降。
5.4.3 带残差连接的ResNet18
5.4.3.1 模型训练
使用带残差连接的ResNet18重复上面的实验,代码如下:
# 学习率大小
lr = 0.01
# 批次大小
batch_size = 64
# 加载数据
train_loader = data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
dev_loader = data.DataLoader(dev_dataset, batch_size=batch_size)
test_loader = data.DataLoader(test_dataset, batch_size=batch_size)
# 定义网络,通过指定use_residual为True,使用残差结构的深层网络
model = Model_ResNet18(in_channels=1, num_classes=10, use_residual=True)
# 定义优化器
optimizer = opt.SGD(lr=lr, params=model.parameters())
# 实例化RunnerV3
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 启动训练
log_steps = 15
eval_steps = 15
runner.train(train_loader, dev_loader, num_epochs=5, log_steps=log_steps,
eval_steps=eval_steps, save_path="best_model.pdparams")
# 可视化观察训练集与验证集的Loss变化情况
plot(runner, 'cnn-loss3.pdf')
运行结果:
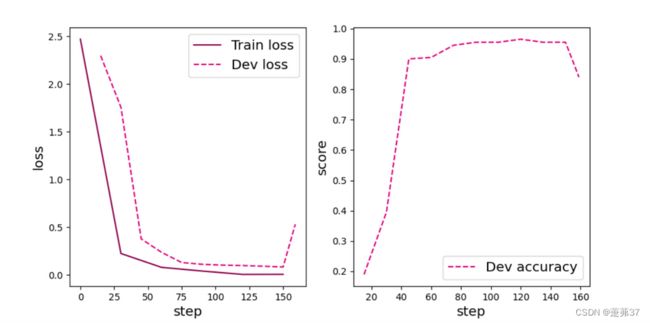
[Train] epoch: 0/5, step: 0/160, loss: 2.46978
[Train] epoch: 0/5, step: 15/160, loss: 0.52145
[Evaluate] dev score: 0.19000, dev loss: 2.29718
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.19000
[Train] epoch: 0/5, step: 30/160, loss: 0.22503
[Evaluate] dev score: 0.39500, dev loss: 1.75715
[Evaluate] best accuracy performence has been updated: 0.19000 --> 0.39500
[Train] epoch: 1/5, step: 45/160, loss: 0.13266
[Evaluate] dev score: 0.90000, dev loss: 0.37835
[Evaluate] best accuracy performence has been updated: 0.39500 --> 0.90000
[Train] epoch: 1/5, step: 60/160, loss: 0.07993
[Evaluate] dev score: 0.90500, dev loss: 0.23769
[Evaluate] best accuracy performence has been updated: 0.90000 --> 0.90500
[Train] epoch: 2/5, step: 75/160, loss: 0.03920
[Evaluate] dev score: 0.94500, dev loss: 0.13020
[Evaluate] best accuracy performence has been updated: 0.90500 --> 0.94500
[Train] epoch: 2/5, step: 90/160, loss: 0.04129
[Evaluate] dev score: 0.95500, dev loss: 0.11184
[Evaluate] best accuracy performence has been updated: 0.94500 --> 0.95500
[Train] epoch: 3/5, step: 105/160, loss: 0.01144
[Evaluate] dev score: 0.95500, dev loss: 0.10348
[Train] epoch: 3/5, step: 120/160, loss: 0.00599
[Evaluate] dev score: 0.96500, dev loss: 0.09905
[Evaluate] best accuracy performence has been updated: 0.95500 --> 0.96500
[Train] epoch: 4/5, step: 135/160, loss: 0.00453
[Evaluate] dev score: 0.95500, dev loss: 0.09177
[Train] epoch: 4/5, step: 150/160, loss: 0.00663
[Evaluate] dev score: 0.95500, dev loss: 0.08366
[Evaluate] dev score: 0.84000, dev loss: 0.53131
[Train] Training done!
5.4.3.2 模型评价
使用测试数据对在训练过程中保存的最佳模型进行评价,观察模型在测试集上的准确率以及损失情况。
# 加载最优模型
runner.load_model('best_model.pdparams')
# 模型评价
score, loss = runner.evaluate(test_loader)
print("[Test] accuracy/loss: {:.4f}/{:.4f}".format(score, loss))
运行结果:
[Test] accuracy/loss: 0.9650/0.1460
添加了残差连接后,模型收敛曲线更平滑。
从输出结果看,和不使用残差连接的ResNet相比,添加了残差连接后,模型效果有了一定的提升。
5.4.4 与高层API实现版本的对比实验
对于Reset18这种比较经典的图像分类网络,飞桨高层API中都为大家提供了实现好的版本,大家可以不再从头开始实现。这里为高层API版本的resnet18模型和自定义的resnet18模型赋予相同的权重,并使用相同的输入数据,观察输出结果是否一致。
import warnings
#warnings.filterwarnings("ignore")
# 使用飞桨HAPI中实现的resnet18模型,该模型默认输入通道数为3,输出类别数1000
hapi_model = resnet18(pretrained=True)
# 自定义的resnet18模型
model = Model_ResNet18(in_channels=3, num_classes=1000, use_residual=True)
# 获取网络的权重
params = hapi_model.state_dict()
# 用来保存参数名映射后的网络权重
new_params = {}
# 将参数名进行映射
for key in params:
if 'layer' in key:
if 'downsample.0' in key:
new_params['net.' + key[5:8] + '.shortcut' + key[-7:]] = params[key]
elif 'downsample.1' in key:
new_params['net.' + key[5:8] + '.shorcutt' + key[23:]] = params[key]
else:
new_params['net.' + key[5:]] = params[key]
elif 'conv1.weight' == key:
new_params['net.0.0.weight'] = params[key]
elif 'bn1' in key:
new_params['net.0.1' + key[3:]] = params[key]
elif 'fc' in key:
new_params['net.7' + key[2:]] = params[key]
# 将飞桨HAPI中实现的resnet18模型的权重参数赋予自定义的resnet18模型,保持两者一致
del new_params[ "net.2.0.shorcutteight"]
del new_params["net.2.0.shorcuttias"]
del new_params["net.2.0.shorcuttunning_mean"]
del new_params["net.2.0.shorcuttunning_var"]
del new_params["net.2.0.shorcuttum_batches_tracked"]
del new_params["net.3.0.shorcutteight"]
del new_params["net.3.0.shorcuttias"]
del new_params["net.3.0.shorcuttunning_mean"]
del new_params["net.3.0.shorcuttunning_var"]
del new_params["net.3.0.shorcuttum_batches_tracked"]
del new_params["net.4.0.shorcutteight"]
del new_params["net.4.0.shorcuttias"]
del new_params["net.4.0.shorcuttunning_mean"]
del new_params["net.4.0.shorcuttunning_var"]
del new_params["net.4.0.shorcuttum_batches_tracked"]
#model.load_state_dict(torch.load("best_model.pdparams"))
#model.load_state_dict(new_params)
# 这里用np.random创建一个随机数组作为测试数据
inputs = np.random.randn(*[3,3,32,32])
inputs = inputs.astype('float32')
x = torch.tensor(inputs)
output = hapi_model(x)
hapi_out = hapi_model(x)
# 计算两个模型输出的差异
diff = output - hapi_out
# 取差异最大的值
max_diff = torch.max(diff)
print(max_diff)
运行结果:
tensor(0., grad_fn=<MaxBackward1>)
可以看到,高层API版本的resnet18模型和自定义的resnet18模型输出结果是一致的,也就说明两个模型的实现完全一样。
学习并在实验中使用:Pytorch torchvision.models
18主要指的是带有权重的,包括卷积层和全连接层,不包括池化层和BN层。(BN层是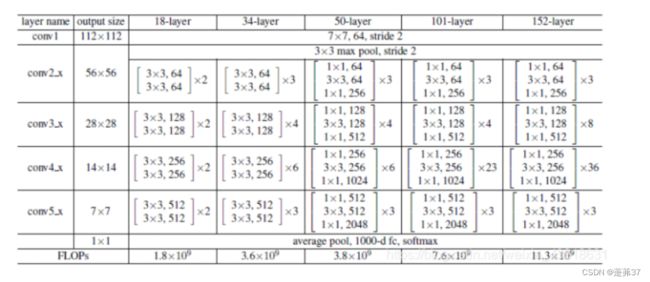
ResNet的前两层跟之前介绍的GoogLeNet中的一样: 在输出通道数为64、步幅为2的7×7卷积层后,接步幅为2的3×33×3的最大汇聚层。 不同之处在于ResNet每个卷积层后增加了批量规范化层。
ResNet则使用4个由残差块组成的模块,每个模块使用若干个同样输出通道数的残差块。 第一个模块的通道数同输入通道数一致。 由于之前已经使用了步幅为2的最大汇聚层,所以无须减小高和宽。 之后的每个模块在第一个残差块里将上一个模块的通道数翻倍,并将高和宽减半。
(注意每个残差块的使用,第一次是通道数的变化,所以加入一层卷积层,第二次通道数不变化,所以不要用到卷积层,直接将输入加到输出)
接着在ResNet加入所有残差块,这里每个模块使用2个残差块
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
def resnet_block(input_channels, num_channels, num_residuals,
first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(Residual(input_channels, num_channels,
use_1x1conv=True, strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))
net = nn.Sequential(b1, b2, b3, b4, b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(), nn.Linear(512, 10))
验证代码:
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape:\t', X.shape)
运行结果:
Sequential output shape: torch.Size([1, 64, 56, 56])
Sequential output shape: torch.Size([1, 64, 56, 56])
Sequential output shape: torch.Size([1, 128, 28, 28])
Sequential output shape: torch.Size([1, 256, 14, 14])
Sequential output shape: torch.Size([1, 512, 7, 7])
AdaptiveAvgPool2d output shape: torch.Size([1, 512, 1, 1])
Flatten output shape: torch.Size([1, 512])
Linear output shape: torch.Size([1, 10])
总结
通过本次实验,了解了ResNet网络,其中18是权重层的数量。通过ResNet经典残差网络完成了Mnist手写数字的识别,体会到残差网络的优越性,对于残差单元有了一定的了解,掌握了残差网络的基本结构。发现随着网络越来越深,训练变得原来越难,网络的优化变得越来越难。理论上,越深的网络,效果更好;但实际上,由于训练难度,过深的网络会产生退化问题,效果反而不如相对较浅的网络。随着网络越来越深,当堆叠到一定网络深度时,就会出现梯度消失或梯度爆炸问题。
参考
resnet18 — Torchvision 0.13 documentation (pytorch.org)
NNDL 实验5(上)
Resnet 18网络模型