01 数据操作
1.数据操作
1.1 N维数组样例
- 0-d(标量)

1.0
一个类别 - 1-d(向量)
![]()
[1.0,2.7,3.4]
一个特征向量
[[[0.1,2.7,3.4]
[5.0,0.5,4.6]
[4.3,8.5,0.2]]
[[3.2,5.7,3.4]
[5.4,6.4,3.2]
[4.1,3.5,6.2]]]
RGB图片
一个视频批量 (批量大小时间宽高通道 )
1.2 创建数组
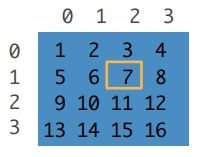
(3)一列:[:,1]
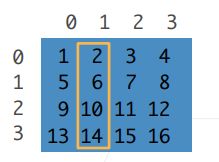
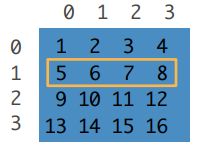
(4)子区域:[1:3,1:] 1-3行不包括第3行,第一列至最后一列
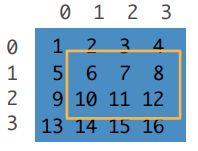
(5)子区域:[::3,::2]选择隔开的元素
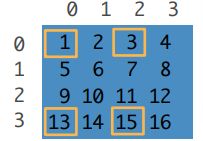
隔3行 隔两列选择元素
数据预处理
import torch
x = range(12)
x
输出:range(0, 12)
x = torch.arange(12)
x
输出:tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
#张量的形状
x.shape
输出:torch.Size([12])
#元素的总数
x.numel()
输出:12
#改变张量的形状
x=x.reshape(3,4)
x
输出:tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
#创建全0张量
torch.zeros((2,3,4))
输出:tensor([[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]])
#创建全1张量
torch.ones((2,3,4))
输出:tensor([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]])
#通过提供包含数值的Python列表来为所需张量中的每个元素赋予确定值
torch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]])
输出:tensor([[2, 1, 4, 3],
[1, 2, 3, 4],
[4, 3, 2, 1]])
#随机生成Tensor中每个元素的值,均值为0,标准差为1的正态分布
torch.randn((3,4))
输出:tensor([[-1.8565, -1.7512, 0.9520, 0.1393],
[ 1.1304, -0.6777, 0.0123, 0.5098],
[ 2.4997, -0.2599, -1.1707, 1.0745]])
#tensor运算
#1.加法
y = torch.ones((3,4))
x+y
输出:tensor([[ 1., 2., 3., 4.],
[ 5., 6., 7., 8.],
[ 9., 10., 11., 12.]])
x*y
输出:tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]])
x.float()/y.float()
输出:tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]])
torch.exp(x.float())
输出:tensor([[1.0000e+00, 2.7183e+00, 7.3891e+00, 2.0086e+01],
[5.4598e+01, 1.4841e+02, 4.0343e+02, 1.0966e+03],
[2.9810e+03, 8.1031e+03, 2.2026e+04, 5.9874e+04]])
#按维度拼接矩阵
torch.cat((x,y),0)
输出:tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.]])
#0为纵向拼接,1为横向拼接
torch.cat((x,y),1)
输出:tensor([[ 0., 1., 2., 3., 1., 1., 1., 1.],
[ 4., 5., 6., 7., 1., 1., 1., 1.],
[ 8., 9., 10., 11., 1., 1., 1., 1.]])
#使用条件判别式可以得到元素为0或1的新的tensor
x==y
输出:tensor([[False, True, False, False],
[False, False, False, False],
[False, False, False, False]])
#tensor元素求和得到只有一个元素的tensor
torch.sum(x)
输出:tensor(66)
#通过item()函数将结果转变换为python中的标量
torch.sum(x).item()
输出:66
#两个形状不同的元素按元素运算可能会触发广播机制
A = torch.arange(0,3).view(3,1)
B = torch.arange(0,2).view(1,2)
A,B
输出:(tensor([[0],
[1],
[2]]),
tensor([[0, 1]]))
#由于A,B分别是3行1列和1行2列的矩阵,如果要计算A+B,那么A中第一列的三个元素被广播到了第2列,B中第一行的2个元素呗广播到了第二行和第三行
A+B
输出:tensor([[0, 1],
[1, 2],
[2, 3]])
#索引 原则:左闭右开
x[1:3]
输出:tensor([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
#指定需要访问的单个元素的位置
x[1,2]= 9
x
输出:tensor([[ 0, 1, 2, 3],
[ 4, 5, 9, 7],
[ 8, 9, 10, 11]])
#截取部分元素
x[1:2,:]
输出:tensor([[4, 5, 9, 7]])
x[1:2,:] = 12
x
输出:tensor([[ 0, 1, 2, 3],
[12, 12, 12, 12],
[ 8, 9, 10, 11]])
#运算的内存开销
before = id(y) #通过判断id是否一致,那么它们所对应的内存地址相同,反之则不同
y = y + x
id(y) == before
输出:False
z = torch.zeros_like(y)
before = id(z)
z[:]= x+y
id(z) == before
输出:True
#避免临时内存开销,使用运算符全名函数中的out参数
torch.add(x,y,out=z)
id(z) == before
输出:True
#如果x的值在之后的程序中不会复用,我们也可以用x[:] = x+y或者x+=y来减少运算内存的开销
before = id(x)
x += y.int()
id(x)==before
输出:True
#tensor和numpy相互变换
import numpy as np
p = np.ones((2,3))
d = torch.from_numpy(p)
d
输出:tensor([[1., 1., 1.],
[1., 1., 1.]], dtype=torch.float64)
d.numpy()
输出:array([[1., 1., 1.],
[1., 1., 1.]])
tensor是pytorch中存储和变换数据的主要工具
d = torch.from_numpy(p)
d
输出:tensor([[1., 1., 1.],
[1., 1., 1.]], dtype=torch.float64)
我们可以通过numpy()和from_numpy()完成转换
d.numpy()
输出:array([[1., 1., 1.],
[1., 1., 1.]])
小结:tensor是pytorch中存储和变换数据的主要工具
可以轻松地对tensor创建、运算、指定索引,并与numpy之间相互变换