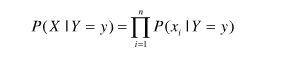基于朴素贝叶斯的文本分类算法
摘要:常用的文本分类方法有支持向量机、K-近邻算法和朴素贝叶斯。其中朴素贝叶斯具有容易实现,运行速度快的特点,被广泛使用。本文详细介绍了朴素贝叶斯的基本原理,讨论多项式模型(MM),实现了可运行的代码,并进行了一些数据测试。
关键字:朴素贝叶斯;文本分类
第1章 贝叶斯原理
1.1 贝叶斯公式[1]
已知某条件概率,如何得到两个事件交换后的概率,也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率:
![]() 表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:
表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。其基本求解公式为:![]() 。
。
贝叶斯定理之所以有用,是因为我们在生活中经常遇到这种情况:我们可以很容易直接得出P(A|B),P(B|A)则很难直接得出,但我们更关心P(B|A),贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。
贝叶斯定理:
1.2 贝叶斯定理在分类中的应用[2]
在分类(classification)问题中,常常需要把一个事物分到某个类别。一个事物具有很多属性,把它的众多属性看做一个向量,即x=(x1,x2,x3,…,xn),用x这个向量来代表这个事物。类别也是有很多种,用集合Y={y1,y2,…ym}表示。如果x属于y1类别,就可以给x打上y1标签,意思是说x属于y1类别。这就是所谓的分类(Classification)。
x的集合记为X,称为属性集。一般X和Y的关系是不确定的,你只能在某种程度上说x有多大可能性属于类y1,比如说x有80%的可能性属于类y1,这时可以把X和Y看做是随机变量,P(Y|X)称为Y的后验概率(posterior probability),与之相对的,P(Y)称为Y的先验概率(prior probability)[2]。
在训练阶段,我们要根据从训练数据中收集的信息,对X和Y的每一种组合学习后验概率P(Y|X)。分类时,来了一个实例x,在刚才训练得到的一堆后验概率中找出所有的P(Y|x),其中最大的那个y,即为x所属分类。根据贝叶斯公式,后验概率为
在比较不同Y值的后验概率时,分母P(X)总是常数,因此可以忽略。先验概率P(Y)可以通过计算训练集中属于每一个类的训练样本所占的比例容易地估计。
1.3朴素贝叶斯分类器
朴素贝叶斯分类是一种十分简单的分类算法,叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素,朴素贝叶斯的思想基础是 这样的:对于给出的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。通俗来说,就好比这么个道理,你在街 上看到一个黑人,我问你你猜这哥们哪里来的,你十有八九猜非洲。为什么呢?因为黑人中非洲人的比率最高,当然人家也可能是美洲人或亚洲人,但在没有其它可 用信息下,我们会选择条件概率最大的类别,这就是朴素贝叶斯的思想基础。
1、条件独立性[3]
给定类标号y,朴素贝叶斯分类器在估计类条件概率时假设属性之间条件独立。条件独立假设可以形式化的表达如下:
其中每个训练样本可用一个属性向量X=(x1,x2,x3,…,xn)表示,各个属性之间条件独立。
比如,对于一篇文章,
Good good study,Day day up.
可以用一个文本特征向量来表示,x=(Good, good, study, Day, day , up)。一般各个词语之间肯定不是相互独立的,有一定的上下文联系。但在朴素贝叶斯文本分类时,我们假设个单词之间没有联系,可以用一个文本特征向量来表示这篇文章,这就是"朴素"的来历。
2、朴素贝叶斯如何工作
有了条件独立假设,就不必计算X和Y的每一种组合的类条件概率,只需对给定的Y,计算每个xi的条件概率。后一种方法更实用,因为它不需要很大的训练集就能获得较好的概率估计。
3、估计分类属性的条件概率
P(xi|Y=y)怎么计算呢?它一般根据类别y下包含属性xi的实例的比例来估计。以文本分类为例,xi表示一个单词,P(xi|Y=y)=包含该类别下包含单词的xi的文章总数/ 该类别下的文章总数。
4、条件概率的m估计
假设有来了一个新样本 x1= (Outlook = Cloudy,Temprature = Cool,Humidity = High,Wind = Strong),要求对其分类。我们来开始计算,
P(Outlook = Cloudy|Yes)=0/9=0 P(Outlook = Cloudy |No)=0/5=0
计算到这里,大家就会意识到,这里出现了一个新的属性值,在训练样本中所没有的。如果有一个属性的类条件概率为0,则整个类的后验概率就等于0,我们可以直接得到后验概率P(Yes | x1)= P(No | x1)=0,这时二者相等,无法分类。
当训练样本不能覆盖那么多的属性值时,都会出现上述的窘境。简单的使用样本比例来估计类条件概率的方法太脆弱了,尤其是当训练样本少而属性数目又很大时。
解决方法是使用m估计(m-estimate)方法来估计条件概率:
n是类yj中的样本总数,nc是类yj中取值xi的样本数,m是称为等价样本大小的参数,而p是用户指定的参数。如果没有训练集(即n=0),则P(xi|yj)=p, 因此p可以看作是在类yj的样本中观察属性值xi的先验概率。等价样本大小决定先验概率和观测概率nc/n之间的平衡。
第一阶段——准备工作阶段,这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要工作是根据具体情况确定特征属性,并对每个特征属性进行适当划分, 然后由人工对一部分待分类项进行分类,形成训练样本集合。这一阶段的输入是所有待分类数据,输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯 一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段——分类器训练阶段,这个阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估 计,并将结果记录。其输入是特征属性和训练样本,输出是分类器。这一阶段是机械性阶段,根据前面讨论的公式可以由程序自动计算完成。
第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类,其输入是分类器和待分类项,输出是待分类项与类别的映射关系。这一阶段也是机械性阶段,由程序完成。
第2章 朴素贝叶斯文本分类算法
现在开始进入本文的主旨部分:如何将贝叶斯分类器应用到文本分类上来。
2.1文本分类问题
在文本分类中,假设我们有一个文档d∈X,X是文档向量空间(document space),和一个固定的类集合C={c1,c2,…,cj},类别又称为标签。显然,文档向量空间是一个高维度空间。我们把一堆打了标签的文档集合
对于这个只有一句话的文档,我们把它归类到 China,即打上china标签。
我们期望用某种训练算法,训练出一个函数γ,能够将文档映射到某一个类别:
γ:X→C
这种类型的学习方法叫做有监督学习,因为事先有一个监督者(我们事先给出了一堆打好标签的文档)像个老师一样监督着整个学习过程。
2.2多项式模型[4]
1、基本原理
在多项式模型中,设某文档d=(t1,t2,…,tk),tk是该文档中出现过的单词,允许重复,则
先验概率P(c)= 类c下单词总数/整个训练样本的单词总数
类条件概率P(tk|c)=(类c下单词tk在各个文档中出现过的次数之和+1)/(类c下单词总数+|V|)
V是训练样本的单词表(即抽取单词,单词出现多次,只算一个),|V|则表示训练样本包含多少种单词。在这里,m=|V|, p=1/|V|。
P(tk|c)可以看作是单词tk在证明d属于类c上提供了多大的证据,而P(c)则可以认为是类别c在整体上占多大比例(有多大可能性)。
2、伪代码
//C,类别集合,D,用于训练的文本文件集合
TrainMultiNomialNB(C,D) {
// 单词出现多次,只算一个
V←ExtractVocabulary(D)
// 单词可重复计算
N←CountTokens(D)
for each c∈C
// 计算类别c下的单词总数
// N和Nc的计算方法和Introduction to Information Retrieval上的不同,个人认为
//该书是错误的,先验概率和类条件概率的计算方法应当保持一致
Nc←CountTokensInClass(D,c)
prior[c]←Nc/N
// 将类别c下的文档连接成一个大字符串
textc←ConcatenateTextOfAllDocsInClass(D,c)
for each t∈V
// 计算类c下单词t的出现次数
Tct←CountTokensOfTerm(textc,t)
for each t∈V
//计算P(t|c)
return V,prior,condprob
}
ApplyMultiNomialNB(C,V,prior,condprob,d) {
// 将文档d中的单词抽取出来,允许重复,如果单词是全新的,在全局单词表V中都
// 没出现过,则忽略掉
W←ExtractTokensFromDoc(V,d)
for each c∈C
score[c]←prior[c]
for each t∈W
if t∈Vd
score[c] *= condprob[t][c]
return max(score[c])
}
3、举例[5]
给定一组分类好了的文本训练数据,如下:
| docId |
doc |
类别 In c=China? |
| 1 |
Chinese Beijing Chinese |
yes |
| 2 |
Chinese Chinese Shanghai |
yes |
| 3 |
Chinese Macao |
yes |
| 4 |
Tokyo Japan Chinese |
no |
给定一个新样本Chinese Chinese Chinese Tokyo Japan,对其进行分类。
该文本用属性向量表示为d=(Chinese, Chinese, Chinese, Tokyo, Japan),类别集合为Y={yes, no}。
类yes下总共有8个单词,类no下总共有3个单词,训练样本单词总数为11,因此P(yes)=8/11, P(no)=3/11。类条件概率计算如下:
P(Chinese | yes)=(5+1)/(8+6)=6/14=3/7
P(Japan | yes)=P(Tokyo | yes)= (0+1)/(8+6)=1/14
P(Chinese|no)=(1+1)/(3+6)=2/9
P(Japan|no)=P(Tokyo| no) =(1+1)/(3+6)=2/9
分母中的8,是指yes类别下textc的长度,也即训练样本的单词总数,6是指训练样本有Chinese,Beijing,Shanghai, Macao, Tokyo, Japan 共6个单词,3是指no类下共有3个单词。
有了以上类条件概率,开始计算后验概率,
P(yes | d)=(3/7)3×1/14×1/14×8/11=108/184877≈0.00058417
P(no | d)= (2/9)3×2/9×2/9×3/11=32/216513≈0.00014780
因此,这个文档属于类别china。
第3章代码详解
本文附带了一个eclipse工程,有完整的源代码,以及一个微型文本训练库。
项目的类图如图所示
文本目录如下图所示:注词库的来源是搜狗的实验室,所以具有较高的实验性
3.1中文分词
中文分词不是本文的重点,这里我们直接使用第三方工具,本源码使用的是MMAnalyzer极易中文分词组件
应该导入
public class ChineseSpliter
{
/**
* 对给定的文本进行中文分词
* @param text 给定的文本
* @param splitToken 用于分割的标记,如"|"
* @return分词完毕的文本
*/
public static String split(String text,String splitToken)
{
}
}
3.2停止词处理
停止词(Stop Word)是指那些无意义的字或词,如"的"、"在"等。去掉文档中的停止词也是必须的一项工作,这里简单的定义了一些常见的停止词,并根据这些常用停止词在分词时进行判断。
public class StopWordsHandler
{
private static String stopWordsList[] ={"的", "我们","要","自己","之","将",""",""",",","(",")","后","应","到","某","后","个","是","位","新","一","两","在","中","或","有","更","好",""};//常用停用词
public static boolean IsStopWord(String word)
{
for(int i=0;i<stopWordsList.length;++i)
{
if(word.equalsIgnoreCase(stopWordsList[i]))
return true;
}
return false;
}
}
3.3预处理数据
把目录放在D://TraninningSet
public class TrainingDataManager
{
private String[] traningFileClassifications;//训练语料分类集合
private File traningTextDir;//训练语料存放目录
private static String defaultPath = "D:\\TrainningSet";
public TrainingDataManager()
{
traningTextDir = new File(defaultPath);
if (!traningTextDir.isDirectory())
{
throw new IllegalArgumentException("训练语料库搜索失败! [" +defaultPath + "]");
}
this.traningFileClassifications = traningTextDir.list();
}
/**
* 返回训练文本类别,这个类别就是目录名
* @return训练文本类别
*/
public String[] getTraningClassifications()
{
return this.traningFileClassifications;
}
/**
* 根据训练文本类别返回这个类别下的所有训练文本路径(full path)
* @param classification 给定的分类
* @return给定分类下所有文件的路径(full path)
*/
public String[] getFilesPath(String classification)
{
}
/**
* 返回给定路径的文本文件内容
* @param filePath 给定的文本文件路径
* @return文本内容
* @throws java.io.FileNotFoundException
* @throws java.io.IOException
*/
public static String getText(String filePath) throws FileNotFoundException,IOException
{
}
/**
* 返回训练文本集中所有的文本数目
* @return训练文本集中所有的文本数目
*/
public int getTrainingFileCount()
{
}
/**
* 返回训练文本集中在给定分类下的训练文本数目
* @param classification 给定的分类
* @return训练文本集中在给定分类下的训练文本数目
*/
public int getTrainingFileCountOfClassification(String classification)
{
}
/**
* 返回给定分类中包含关键字/词的训练文本的数目
* @param classification 给定的分类
* @param key 给定的关键字/词
* @return给定分类中包含关键字/词的训练文本的数目
*/
public int getCountContainKeyOfClassification(String classification,String key)
{
}
3.3训练
public class PriorProbability
{
private static TrainingDataManager tdm =new TrainingDataManager();
/**
* 先验概率
* @param c 给定的分类
* @return给定条件下的先验概率
*/
public static float calculatePc(String c)
{
float ret = 0F;
float Nc = tdm.getTrainingFileCountOfClassification(c);
float N = tdm.getTrainingFileCount();
ret = Nc / N;
return ret;
}
}
public class ClassConditionalProbability
{
private static TrainingDataManager tdm = new TrainingDataManager();
private static final float M = 0F;
/**
* 计算类条件概率
* @param x 给定的文本属性
* @param c
* @return给定条件下的类条件概率
*/
public static float calculatePxc(String x, String c)
{
float ret = 0F;
float Nxc = tdm.getCountContainKeyOfClassification(c, x);
float Nc = tdm.getTrainingFileCountOfClassification(c);
float V = tdm.getTraningClassifications().length;
ret = (Nxc + 1) / (Nc + M + V);
return ret;
}
}
3.4分类
/**
* 分类结果
*/
public class ClassifyResult
{
public double probility;//分类的概率
public String classification;//分类
public ClassifyResult()
{
this.probility = 0;
this.classification = null;
}
}
public class BayesClassifier
{
private TrainingDataManager tdm;//训练集管理器
private String trainnigDataPath;//训练集路径
private static double zoomFactor = 10.0f;
/**
* 默认的构造器,初始化训练集
*/
public BayesClassifier()
{
tdm =new TrainingDataManager();
}
/**
* 计算给定的文本属性向量X在给定的分类Cj中的类条件概率
* ClassConditionalProbability连乘值
* @param X 给定的文本属性向量
* @param Cj 给定的类别
* @return分类条件概率连乘值,即
*/
float calcProd(String[] X, String Cj)
{
}
/**
* 去掉停用词
* @param text 给定的文本
* @return去停用词后结果
*/
public String[] DropStopWords(String[] oldWords)
{
}
/**
* 对给定的文本进行分类
* @param text 给定的文本
* @return分类结果
*/
@SuppressWarnings("unchecked")
public String classify(String text)
{
//返回概率最大的分类
return crs.get(0).classification;
}
}
测试数据
"新华网天津7月7日体育专电(记者张泽伟)7日,权健集团与天津松江俱乐部联合召开新闻发布会,宣布权健集团正式全资收购松江俱乐部。权健集团董事长束昱辉表示,投资足球将不留余力、不留私心,要做就做最好。未来俱乐部的发展目标将分四步走:保级、冲超、参加亚冠、参加世俱杯。"
测试结果
更多细节请读者阅读源代码。
References:
[1]. 李维杰与徐勇, 简体中文垃圾邮件分类的实验设计及对比研究. 计算机工程与应用, 2007. 43(25): 第128-132页.
[2]. 黄志刚, 基于贝叶斯的中文垃圾邮件过滤系统的设计与实现, 2007, 电子科技大学.
[3]. 马世军, 姚建与乔文, 基于贝叶斯理论的垃圾邮件过滤技术. 硅谷, 2009(13): 第58页.
[4]. 陆青梅与尹四清, 基于贝叶斯定理的垃圾邮件分类技术研究. 信息技术, 2008(2): 第118-120页.
[5]. 王科, 基于贝叶斯的中文邮件分类关键技术研究, 2008, 南京邮电大学.