离散数学 --- 谓词逻辑 --- 谓词合式公式推理

第一部分 --- 推理形式和推理规则

1.谓词在拥有命题演算的基本蕴含公式的同时，还有着自己独有的基本蕴含公式

 

 当我们的描述在个体和整体之间转换时，就需要进行量词的消去和添加

 1.全称特指规则 --- US规则 --- 其实就是全称量词消去规则

2.全称量词消去有上面两种形式：
第一种消去全称量词的方式是代入任意一个属于给定个体域的个体变量（这个个体变量不能够被消掉全称量词后剩下的量词约束）

第二种消去全称量词的方式是代入任意一个属于给定个体域的个体常量

1.存在特指规则 ---ES规则 --- 就是用来消去存在量词的规则

2.关于函数替换 --- 下面的例子中的最后一行就是所谓的函数替换，如果我们不用关于这些变元的函数替换掉C的话，就会导致我们描述的是变量和常量之间的关系，这样的话无论如何描述都会导致描述错误。

所以我们要从根本上解决这个问题，将常量C也变为变量，且这个变量是和除常量C外的变元有关的变量 --- 获得这个变量的方法就是使用关于这些变量的函数来替换常量C --- f（除C以外的变元）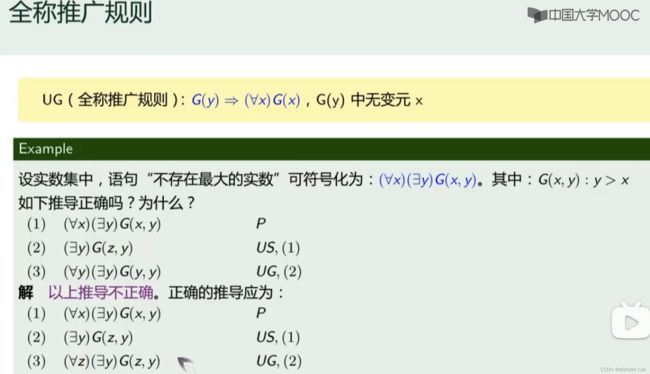

1.如果对于任意一个属于个体域的个体变量都能够为真的话，则在整个个体域中都为真

2.G(y)中无变元x的意思是：避免上面这种符号重复带来的歧义

1.在个体域有一个特定的个体常量能使公式成立 ，则能推出在个体域中存在个体常量使得公式成立

2.在个体域中任意一个个体变量能使公式成立，则也能推出在个体域中存在个体常量使得公式成立

---

第二部分 --- 综合推理方法

1.P表示的是前提，T表示的是通过前提/中间结果推导出的结果

2.规则CP是附加前提规则

3.间接证明方法是反证法

4.没量词就用命题演算中的基本等价公式和基本蕴涵公式，有量词就用谓词中的基本演绎公式和基本蕴涵公式

1.P能推出Q，则P存在的时候Q也存在，但是上面的H(y)不等于H(s)，所以用原来的（2）式是推不出结论的，除非我们把（2）式中的H(y)修改为H(s)（ M(y)也同理 ）

1.如果不是通过存在特指规则（ES）来得到一个个体常量，而是通过全称特指规则得到一个个体常量的话，这个个体常量是任意的且对于全称量词而言是满足的，但由于它是任意的，也就是说它不一定满足存在推广（特指）规则能使公式成立的要求

此时如果用这个个体常量 + 存在推广规则来推回存在量词的话就可能导致错误

所以正确的步骤是先用存在特指规则指定一个个体常量，这样不经存在推广规则能用这个个体常量，全称推广（特指）规则也能使用这个个体常量

2.三步走战略：

1.利用特指规则消去量词

2.进行推导

3.利用推广规则找回量词

1.I是基本蕴涵公式，E是基本等价公式（Equal）

1.首先在无论是否使用反证法，前提都为真，然后反证法的步骤：

一.将结论的否定作为附加前提

二.通过结论的否定推出前提的否定

三.前提的否定为真和前提为真的同时存在 ---> 构成矛盾式，也就是说我们通过结论的否定会推出一个矛盾式（永假公式），也就是说结论的否定为假 ---> 则结论为真 ---> 反证结束

（ps:在前提中没有假的情况下，我们通过前提推出的中间结果和结论都为真，如果前提中有假的情况的话，则根据前提推出的中间结果和结论都为假）