SegFormer阅读笔记

前言

SegFormer是2021年发表在NeurIPS的论文， 在Transformer做语义分割的开篇之作——SETR的基础上进行创新，针对SETR的不足之处进行改进。在ADE20K、Cityscapes和COCO-Stuff三个公开数据集上进行测试，其运行效率、准确性和鲁棒性都达到了SOTA的水平。

如下图，横坐标是参数量（单位：百万），纵坐标是ADE20K上的mean IoU。可以看到，与FCN、DeeplabV3、SETR等模型相比，SegFormer在提升了mIoU的同时，参数量大大减少，大幅提升了运行效率。

并且在Cityscape-C(对测试图像加各种噪声)上，也大幅度超过了之前的方法（DeeplabV3等），这反映了SegFormer良好的鲁棒性。

1. 模型的特点

SETR使用完全的ViT结构作为backbone，然后使用CNN解码器进行上采样完成分割任务，取得了不错的效果，但是，仍有以下缺点：

• ViT backbone只能输出单尺度低分辨率的特征图，而不是多尺度的
• 计算量大。每个像素都要和其他所有像素做匹配计算。

为了解决第一个问题，PVT模型基于ViT提出了金字塔结构。但是，PVT就像Swin Transformer和Twins这些模型一样，还是采用了Positional Embedding操作，测试时需要插值，不够灵活。

SegFormer主要做了如下几项创新：

• 之前ViT和PVT做patch embedding时，每个patch都是独立的，而SegFormer对patch设计成有重叠的，保证局部连续性。
• 使用了多尺度特征融合。Encoder输出多尺度的特征，Decoder将多尺度的特征融合在一起。好处：模型能够同时捕捉高分辨率的粗略特征和低分辨率的细小特征，优化分割结果。
• 舍弃了ViT和SETR中的position embedding位置编码，取而代之的是Mix FFN。好处：在测试图片大小与训练集图片大小不一致时，不需要再对位置向量做双线性插值。
• 轻量级的Decoder。好处：使得Decoder的计算量和参数量非常小，从而使得整个模型可以高效运行，简单直接。并且，通过聚合不同层的信息，结合了局部和全局注意力

2. 模型结构

如下图所示，SegFormer可以分为两个部分：

• 用于生成多尺度特征的分层Encoder。
• 轻量级的All-MLP Decoder，融合多层特征并上采样，最终解决分割任务。
  

输入一张大小$H\times W\times 3$的图片，首先将其划分为大小$4\times 4$的patches。对比ViT和SETR中使用的大小$16\times 16$的patches，使用更小的patches有利于进行分割任务。（由于是预测图像中的每个像素，语义分割又被称为dense prediction密集预测）。

使用这些patches作为Encoder的输入，获取大小为$\frac{H}{4}\times \frac{W}{4}\times C_1$、$\frac{H}{8}\times \frac{W}{8}\times C_2$、$\frac{H}{16}\times \frac{W}{16}\times C_3$、$\frac{H}{32}\times \frac{W}{32}\times C_4$的多尺度的特征图。

将这些多尺度特征输入到解码器中，经过一系列MLP和上采样操作，最终输入大小$\frac{H}{4}\times \frac{W}{4}\times N_{cls}$的特征图，其中$N_{cls}$是类别个数。

2.1 Encoder

Encoder是由Transformer Block堆叠起来的，其中包含Efficient Self-Attention、Mix-FFN和Overlap Patch Embedding三个模块。

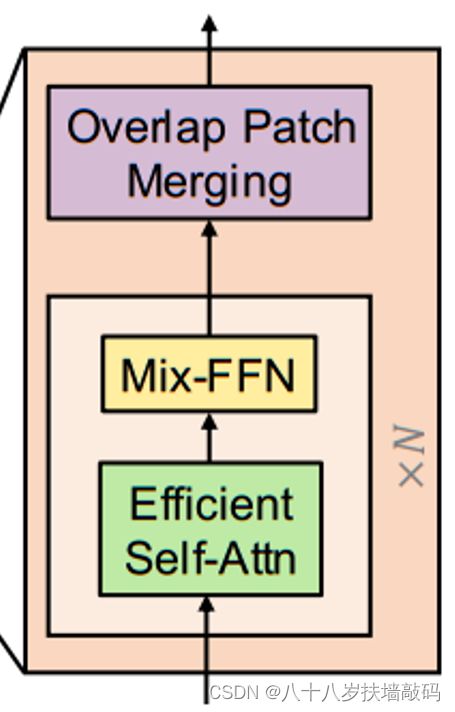
• Overlapped Patch Merging

为了产生类似于CNN backbone的多尺度特征图，SegFormer使用了patch merging的方法，通过$H\times W\times 3$的输入图像，得到大小$\frac{H}{2^{i+1}}\times \frac{W}{2^{i+1}}\times C_i$的多尺度特征图，其中$i\in 1,2,3,4$，并且$C_{i+1}$要比$C_i$大。

ViT中的patch merging可以将$2\times 2\times C_i$的特征图合并成为$1\times 1\times C_{i+1}$的向量来达到降低特征图分辨率的目的。SegFormer同样使用这种方法，将分层特征从$F_1(\frac{H}{4}\times \frac{W}{4}\times C_1)$缩小到$F_2(\frac{H}{8}\times \frac{W}{8}\times C_2)$，同样的方法可以得到$F_3$，$F_4$。但是由于ViT中的patch是不重叠的，会丢失patch边界的连续性，因此SegFormer在切割patch时采用了重叠的patch。切割方法类似于卷积核在feature map上的移动卷积，源代码中也是采用卷积来实现，设置卷积核大小（K），步距（S），填充大小（P）。

第一个Transformer Block的Patch Merging设置为$K=7,S=4,P=3$，这样输出特征图大小变成输入特征图大小的$\frac{1}{4}$。
之后三个Transformer Block的Patch Merging设置为$K=3,S=2,P=1$，输出特征图大小变为输入特征图大小的$\frac{1}{2}$。
这样最终就得到了分辨率分别是$\frac{H}{4}\times \frac{W}{4}\times C_1$、$\frac{H}{8}\times \frac{W}{8}\times C_2$、$\frac{H}{16}\times \frac{W}{16}\times C_3$、$\frac{H}{32}\times \frac{W}{32}\times C_4$的多尺度的特征图。

class MixVisionTransformer(nn.Module):
    def __init__(self, ...):
        super().__init__()
        self.patch_embed1 = OverlapPatchEmbed(img_size=img_size, patch_size=7, stride=4, 
                                              in_chans=in_chans, embed_dim=embed_dims[0])

        self.patch_embed2 = OverlapPatchEmbed(img_size=img_size // 4, patch_size=3, stride=2, 
                                              in_chans=embed_dims[0], embed_dim=embed_dims[1])

        self.patch_embed3 = OverlapPatchEmbed(img_size=img_size // 8, patch_size=3, stride=2,
                                              in_chans=embed_dims[1], embed_dim=embed_dims[2])

        self.patch_embed4 = OverlapPatchEmbed(img_size=img_size // 16, patch_size=3, stride=2, 
                                              in_chans=embed_dims[2], embed_dim=embed_dims[3])



class OverlapPatchEmbed(nn.Module):
    def __init__(self, img_size=224, patch_size=7, stride=4, in_chans=3, embed_dim=768):
        super().__init__()
        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=stride, padding=(patch_size[0] // 2, patch_size[1] // 2))
        self.norm = nn.LayerNorm(embed_dim)
    

    def forward(self, x):
    x = self.proj(x)
    _, _, H, W = x.shape
    x = x.flatten(2).transpose(1, 2)
    x = self.norm(x)

    return x, H, W 

• Efficient Self-Attention

Transformer的计算量之所以大，主要是因为其Self-Attention的计算。
$$Attention(Q,K,V)=Softmax(\frac{Q{K}^T}{\sqrt{d_{h}ead}})V$$
对应multi-head self-attention来说，每一个head的Q、K、V都是相同维度$N\times C$，其中$N=H\times W$是序列的长度。这个过程的计算复杂度是$O(N^2)$，对于高分辨率的图像来说这是无法计算的。

为了减少计算量，作者采用了PVT模型中使用的spatial reduction操作。输入维度$N\times C$的$K$矩阵通过Reshape变成$\frac{N}{R}\times (C\cdot R)$的大小。然后通过线性变换，将$(C\cdot R)$的维度变为$C$。这样输出的$K$大小就变成了$\frac{N}{R}\times C$
$$\hat{K}=Reshape(\frac{N}{R},C\cdot R)(K)$$
$$K=Linear(C\cdot R,C)(\hat{K})$$
对$V$矩阵也进行同样的同样的操作，这样计算复杂度就变成了$O(\frac{N^2}{R})$。论文中四个Transformer Block分别将R设置成了$[64,16,4,1]$。源代码中使用卷积实现。

class Attention(nn.Module):
    def __init__(self, dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0., sr_ratio=1):
        super().__init__()
        assert dim % num_heads == 0, f"dim {dim} should be divided by num_heads {num_heads}."

        self.dim = dim
        self.num_heads = num_heads
        head_dim = dim // num_heads
        self.scale = qk_scale or head_dim ** -0.5

        self.q = nn.Linear(dim, dim, bias=qkv_bias)
        self.kv = nn.Linear(dim, dim * 2, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)

        self.sr_ratio = sr_ratio
        if sr_ratio > 1:
            self.sr = nn.Conv2d(dim, dim, kernel_size=sr_ratio, stride=sr_ratio)
            self.norm = nn.LayerNorm(dim)

        self.apply(self._init_weights)

    def _init_weights(self, m):
        if isinstance(m, nn.Linear):
            trunc_normal_(m.weight, std=.02)
            if isinstance(m, nn.Linear) and m.bias is not None:
                nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.LayerNorm):
            nn.init.constant_(m.bias, 0)
            nn.init.constant_(m.weight, 1.0)
        elif isinstance(m, nn.Conv2d):
            fan_out = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
            fan_out //= m.groups
            m.weight.data.normal_(0, math.sqrt(2.0 / fan_out))
            if m.bias is not None:
                m.bias.data.zero_()

    def forward(self, x, H, W):
        B, N, C = x.shape
        q = self.q(x).reshape(B, N, self.num_heads, C // self.num_heads).permute(0, 2, 1, 3)

        if self.sr_ratio > 1:
            x_ = x.permute(0, 2, 1).reshape(B, C, H, W)
            x_ = self.sr(x_).reshape(B, C, -1).permute(0, 2, 1)
            x_ = self.norm(x_)
            kv = self.kv(x_).reshape(B, -1, 2, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        else:
            kv = self.kv(x).reshape(B, -1, 2, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        k, v = kv[0], kv[1]

        attn = (q @ k.transpose(-2, -1)) * self.scale
        attn = attn.softmax(dim=-1)
        attn = self.attn_drop(attn)

        x = (attn @ v).transpose(1, 2).reshape(B, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)

        return x

• Mix-FFN

作者认为在语义分割任务中实际上并不需要position encoding，采用Mix-FFN替代。Mix-FFN假设0 padding操作可以汇入位置信息，直接用0 padding的$3\times 3$卷积来达到这一目的：
$$x_{out}=MLP(GELU(Con{v}_{3\times 3}(MLP(x_{i}n))))+x_{in}$$
源码如下：

class Mlp(nn.Module):
    ...
    def forward(self, x, H, W):
        x = self.fc1(x)        # nn.Linear(in_features, hidden_features)
        x = self.dwconv(x, H, W)   # DWConv(hidden_features)
        x = self.act(x)        # GELU
        x = self.drop(x)       # dropout
        x = self.fc2(x)        # nn.Linear(hidden_features, out_features)
        x = self.drop(x)
        return x

# DWConv define as follows
class DWConv(nn.Module):
    def __init__(self, dim=768):
        super(DWConv, self).__init__()
        # 3x3 Conv with zero padding
        self.dwconv = nn.Conv2d(dim, dim, 3, 1, 1, bias=True, groups=dim)

    def forward(self, x, H, W):
        B, N, C = x.shape
        x = x.transpose(1, 2).view(B, C, H, W)
        x = self.dwconv(x)
        x = x.flatten(2).transpose(1, 2)

        return x

2.2 Decoder

SegFormer的Decoder是一个仅由MLP层组成的轻量级Decoder，之所以能够使用这种简单结构，关键在于分层Transformer编码器具有比传统CNN编码器更大的有效感受野（ERF）。Decoder结构如下图：

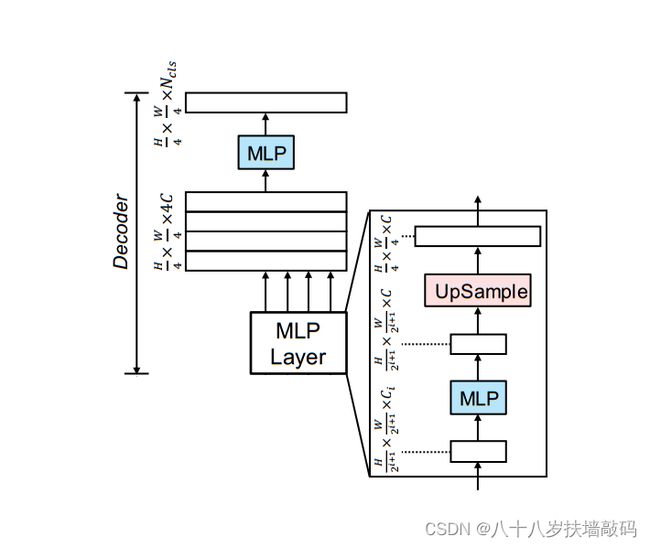
All-MLP Decoder包含四个主要步骤：

1. 来自Encoder的四个不同分辨率的特征图$F_i$分别经过MLP层使得通道维度相同。
   $$\widehat{F_i}=Linear(C_i,C)(F_i),\forall i$$
2. 将特征图分别进行双线性插值上采样到原图的$\frac{1}{4}$，并拼接在一起。
   $$\widehat{F_i}=Upsample(\frac{W}{4}\times \frac{W}{4})(\widehat{F_i}),\forall i$$
3. 使用MLP层来融合级联特征。（卷积）
   $$F=Linear(4C,C)(Concat(\widehat{F_i})),\forall i$$
4. 使用另外一个MLP层采用融合特征图输出最终$\frac{H}{4}\times \frac{W}{4}\times N_{cls}$的预测特征图。（卷积）其中$N_{c}ls$是类别数。
   $$M=Linear(C,N_{cls})(F)$$

3. 思考与分析

对于语义分割来说最重要的问题就是如何增大有效感受野。对于CNN Encoder来说，有效感受野是比较小且局部的，所以需要一些decoder的设计来增大有效感受野，比如ASPP中利用了不同大小的膨胀卷积来实现这一目的。

但对于Transformer encoder来说，由于self-attention，有效感受野变得非常大，因此decoder不需要更多操作来提高有效感受野，也因此可以设计更加简单的decoder。

如下图，对DeepLabV3+和SegFormer的四个Encoder阶段和Decoder Head的有效感受野进行了可视化。

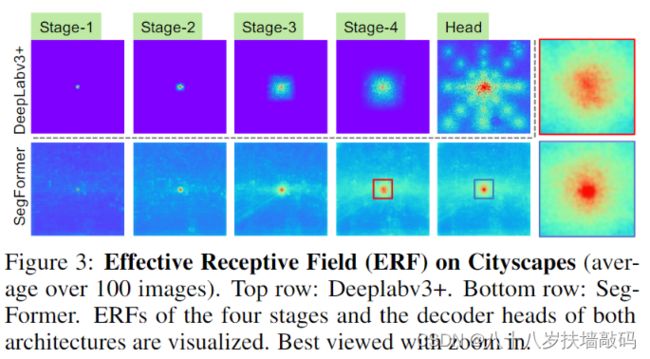
从图中可以看出：

• DeepLabv3+即使在卷积深度最深的第四层有效感受野也很小。
• SegFormer的Encoder天生就能在浅层产生类似于卷积的局部注意力，同时也能输出高度非局部的注意力（全局注意力），从而在第4阶段有效捕获上下文。
• 在最后放大的Decoder Head的有效感受野中可以看到，除了有全局注意力外，SegFormer明显比DeepLabv3有更强的局部注意力。

4. 下一步计划

下一步计划

• 学习DeepLab系列论文及代码实现
• 阅读PVT论文及源码，整理模型结构
• 整理过去几周学习的模型的源码，尝试复现并加上分割头，解决分割任务。

参考

1. （NeurIPS’21) SegFormer: 简单有效的语义分割新思路
2. 论文笔记——Segformer: 一种基于Transformer的语义分割方法
3. Segformer 论文笔记