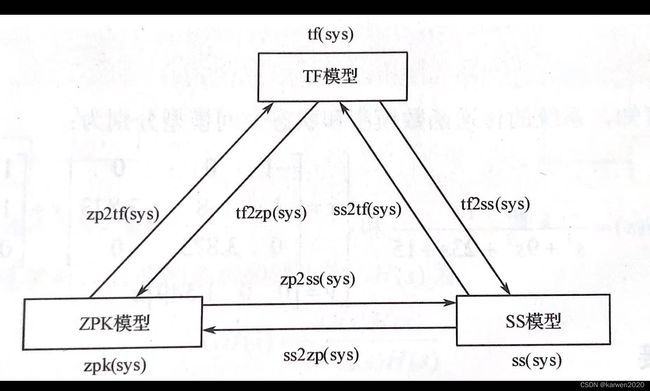
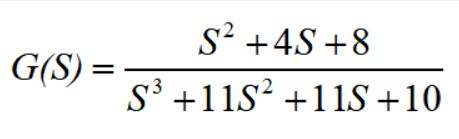使用Matlab进行传递函数、状态空间、零极点的建模与转换
一.模型建立
- 1、传递函数模型
num=[1,4,8];
den=[1,11,11,10];
G=tf(num,den)
提取传递函数分子、分母中系数:
[num,den]=tfdata(G,‘V’)
'V’为关键词,功能是返回列向量形式的分子分母多项式系数
求多项式的根:
r=roots( p)
p——多项式降幂排列的系数行向量
r——所求根列向量
由根创建多项式函数:
p=poly( r )
- 2、状态空间模型
A=[ -11 -11 -10;
1 0 0;
0 1 0]
B=[1;
0;
0];
C= [1 4 8];
D=0;
sys=ss(A,B,C,D);
提取状态空间矩阵:
[A,B,C,D]=ssdata(sys)
- 3、零极点模型
sys=zpk([z],[p],[k])
提取零极点和增益向量:
[z,p,k]=zpkdata(sys,‘V’)
- 4、传递函数部分分式展开
[r,p,k]=residue(b,a)
r——余数向量
p——极点列向量
k——常数项
b,a——按S的降幂排列的多项式
G(S)=K+∑ri/(s-pi),i=1,2,3……
设传递函数为:G(S)=6(S+2)/[(s+1)(s+3)(s+5)]
z=[-2];
p=[-1,-3,-5];
k=6;
[num,den]=zp2tf(z,p,k) %零极点转传递函数
[A,B,C,D]=zp2ss(z,p,k) %零极点转状态空间
s_zpk=zpk(z,p,k)
s_tf=tf(num,den)
s_ss=ss(A,B,C,D)