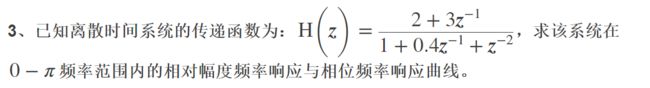MATLAB_数字信号处理_04_离散系统的描述模型和频率响应分析
SYSU_SECE_数字信号处理_04
离散系统的描述模型和频率响应分析

部分原理:
1.一个线性移不变(LSI)离散系统可以用线性常系数差分方程表示,这是系统在时域的表达式;对差分方程两边进行z变换,得到离散LSI系统的系统传递函数(tf)模型;对系统传递函数(tf)模型进行因式分解可以得到系统传递函数的零-极点增益(zpk)模型;当zpk模型中的极点均为单极点时,可以将其分解为部分分式,表示为系统的极点留数(rpk)模型;离散LSI系统函数经常包含复数的零、极点,把每一对共轭零点或共轭极点多项式合并,就可以得到二次分式(sos)模型;另外还有状态变量(ss)模型。
2.一个离散系统的因果性在时域中必须满足的充分必要条件是:H(n)=0 n<0,即系统的冲激响应必须是右序列。在变换域,极点只能位于z平面上一个有界的以原点为中心的圆内。
稳定性:充要条件是冲激响应绝对可加,在变换域,即所有极点位于z平面上以原点为中心的单位圆内。
因果稳定系统充要条件:系统函数的全部极点必须在z平面上以原点为中心的单位圆内。
3.系统函数与频率响应有着密切的联系,适当的控制系统函数的极点、零点的分布,可以改变离散系统的频率响应特性:
(1)在原点(z=0)处的零点或极点至单位圆的距离始终保持不变,其值等于1,所以对幅度相应不起作用。
(2)单位圆附近的零点对系统幅度响应的凹谷位置及深度有明显的影响。
(3)单位圆内且靠近单位圆附近的极点对系统幅度响应的凸峰的位置及峰度有明显的影响。

num=[2,3,0];
den=[1,0.4,1];
%part1___zpk模型
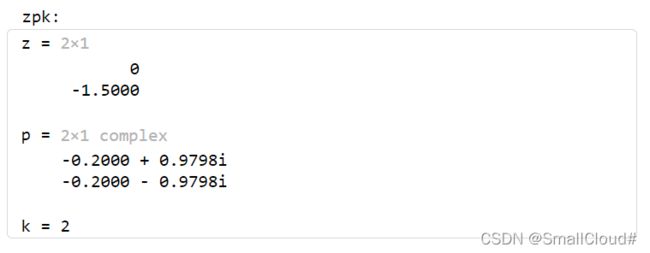
disp('zpk:')
[z,p,k]=tf2zp(num,den)
%part2___sos模型
disp('sos:')
[sos,g]=tf2sos(num,den)
%part3___rpk模型
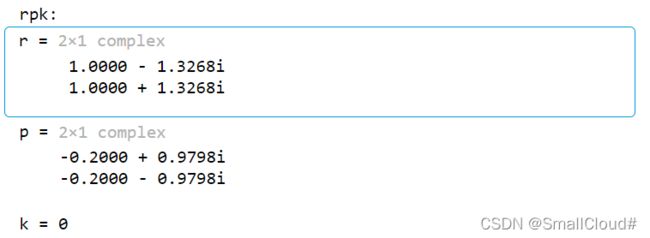
disp('rpk:')
[r,p,k]=residuez(num,den)
%part4___ss模型
disp('ss:')
[A,B,C,D]=tf2ss(num,den)
disp('题目二(1):')
figure(1)
%根据公式写出zpk列向量的形式
z1=0.3;p1=[-0.5+0.7j,-0.5-0.7j]';k=1;
[b1,a1]=zp2tf(z1,p1,k);
subplot(2,1,1),zplane(b1,a1);
subplot(2,1,2),impz(b1,a1,50);
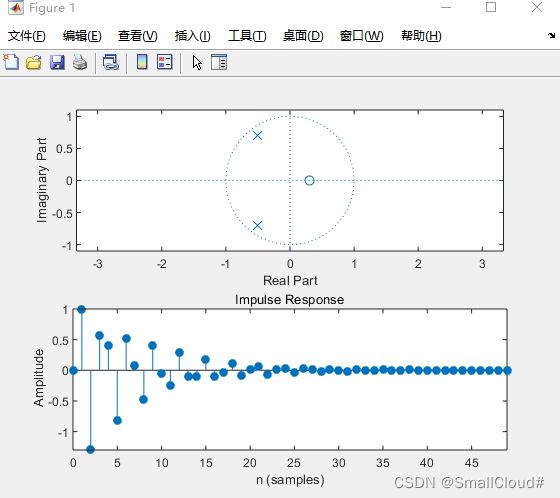
disp('题目二(2):')
figure(2)
z2=0.3;p2=[-0.6+0.8j,-0.6-0.8j]';k=1;
[b2,a2]=zp2tf(z2,p2,k);
subplot(2,1,1),zplane(b2,a2);
subplot(2,1,2),impz(b2,a2,50);
disp('H2(z)')
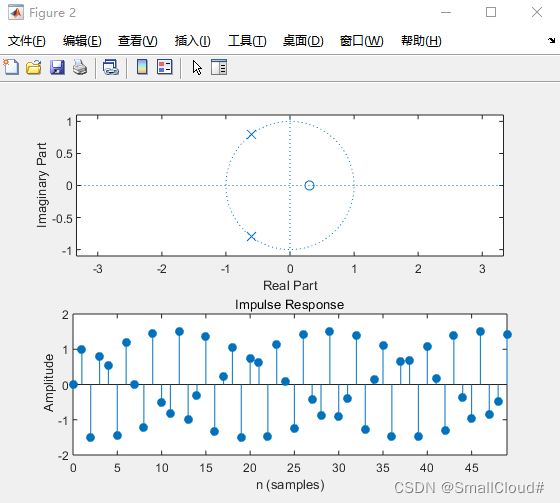
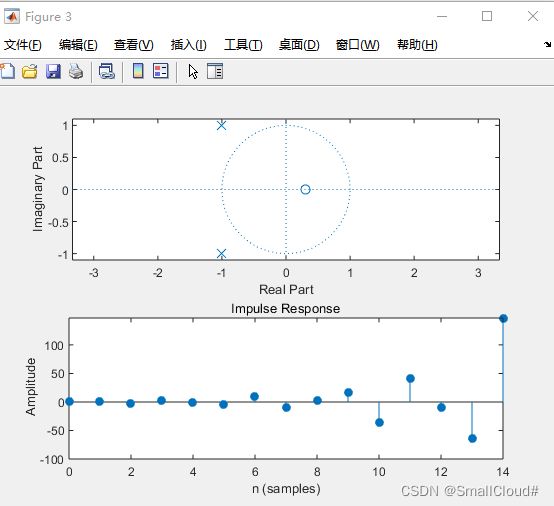
disp('题目二(3):')
figure(3)
z3=0.3;p3=[-1+j,-1-j]';k=1;
[b3,a3]=zp2tf(z3,p3,k);
subplot(2,1,1),zplane(b3,a3);
subplot(2,1,2),impz(b3,a3,15);
disp('三个系统的极点均为复数且处于z平面的左半平面;')
disp('H1(z)的两个极点处于单位圆内,是因果稳定系统,系统的冲激响应曲线随着频率的增大而收敛;')
disp('H2(z)的两个极点处于单位圆上,不是因果稳定系统,系统的冲激响应曲线为等幅振荡;')
disp('H3(z)的两个极点处于单位圆内,不是因果稳定系统,系统的冲激响应曲线随着频率的增大而发散。')
disp('结论:系统只有极点处于单位圆内才是稳定的')
figure(4)%使用freqz直接绘制幅频和相频特性曲线
b=[2,3,0];
a=[1,0.4,1];
freqz(b,a);
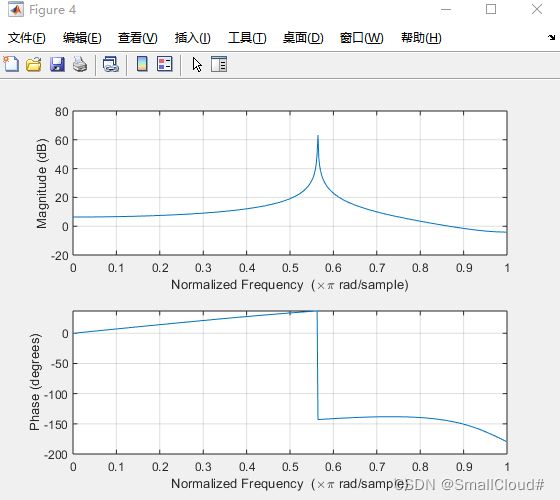
figure(5)
%首先将zpk模型转换为tf模型
z=[0,-2]';p=[0.3,0.4,0.6]';k=1;
[num,den]=zp2tf(z,p,k)
n=(0:500)*pi/500;
[h,w]=freqz(num,den,n);
db=20*log10(abs(h));%求相对幅频响应值
subplot(2,2,1),plot(w/pi,abs(h));title('幅频特性(V)');grid on
subplot(2,2,2),plot(w/pi,angle(h));title('相频特性');grid on
subplot(2,2,3),plot(w/pi,db);title('幅频特性(dB)');grid on
subplot(2,2,4),zplane(num,den);title('零极点分布');
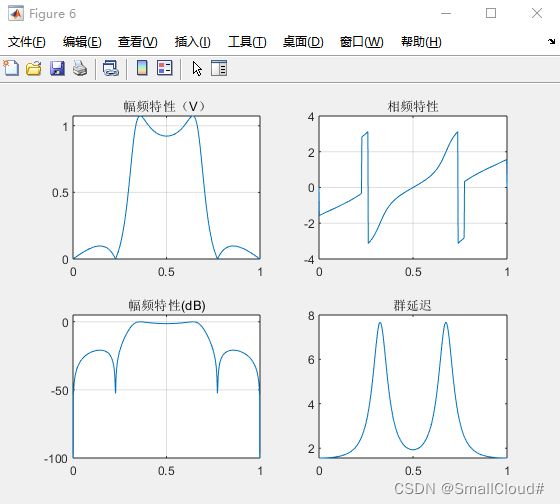
figure(6)
b=[0.187632,0,-0.241242,0,0.241242,0,-0.187632];
a=[1,0,0.602012,0,0.495684,0,-0.035924];
[H,w]=freqz(b,a,1000,'whole');
H=(H(1:501))';w=(w(1:501))';
mag=abs(H);
db=20*log10((mag+eps)/max(mag));
pha=angle(H);
grd=grpdelay(b,a,w);
subplot(2,2,1),plot(w/pi,mag);title('幅频特性(V)');grid on
subplot(2,2,2),plot(w/pi,pha);title('相频特性');grid on
subplot(2,2,3),plot(w/pi,db);title('幅频特性(dB)');axis([0,1,-100,5]);grid on
subplot(2,2,4),plot(w/pi,grd);title('群延迟');
% 以上程序所用到的MATLAB函数
% tf2zp 将系统传递函数(tf)模型转换为系统函数的零-极点增益(zpk)模型
% zp2tf 将zpk模型转换为tf模型
% tf2sos 将tf模型转换为二次分式(sos)模型
% tf2ss 将tf模型转换为系统状态空间(ss)模型
% residuez 将tf模型转换为极点留数(rpk)模型
% zplane 显示离散系统的零极点分布图
% freqz 求解离散时间系统的频率响应函数
% freqz(b,a,n) 绘制幅频和相频特性曲线
% angle 求相角
% angle(h) 用于求取复矢量或复矩阵H的相角(以弧度为单位)
% grid 在指定的图形坐标上绘制分格线