吴恩达-机器学习课后题06-SVM(支持向量机)1-线性可分

1、概念

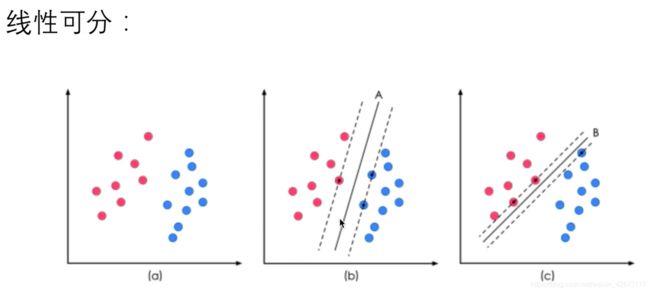
1、支持向量机：支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
参考自：https://zhuanlan.zhihu.com/p/31886934

2、直观理解

支持向量机取自最佳分类线

3、SVM的损失函数及其梯度

2、支持库

1、Scikit-learn

2、题目

1、任务：观察C(误差函数中的惩罚系数)的取值对决策边界的影响

3、解题

0、使用库：

import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
from sklearn.svm import SVC

注意新导入了SVM库中的SVC

1、导入数据

data = sio.loadmat(path)
# print(data.keys())
X,y = data['X'],data['y']
# print(y.flatten())
# print(X.shape,y.shape)

2、数据可视化

def plot_data():
    plt.scatter(X[:,0],X[:,1],c=y.flatten(),cmap='jet')
    #使用y的取值进行将x0，x1区分，然后使用将其按jet颜色(蓝红配色)映射方式进行展示
    plt.xlabel('x1')
    plt.ylabel('y1')
    plt.show()

plot_data()

注意使用的方式是c=y.flatten()

结果：

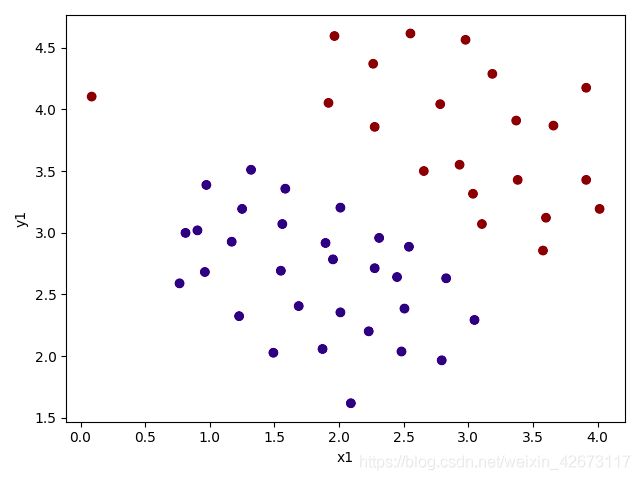
可以看出，数据中的两种类型是线性可分的，但是有一个特殊点

3、sclearn.svm中svc的使用方法

3、建立分类器

#实例化一个分类器
svc1 = SVC(C=1,kernel='linear')
svc1.fit(X,y.flatten())
print(svc1.predict(X))
score = svc1.score(X,y.flatten())
print(score)

结果：
0.9803921568627451

4、输出预测曲线：

def plot_boundary(model):
    x_min,x_max = -0.5,4.5
    y_min,y_max = 1.3,5
    xx,yy = np.meshgrid(np.linspace(x_min,x_max,500),
                        np.linspace(y_min,y_max,500))
    z = model.predict(np.c_[xx.flatten(),yy.flatten()])
    zz = z.reshape(xx.shape)
    plt.contour(xx,yy,zz)
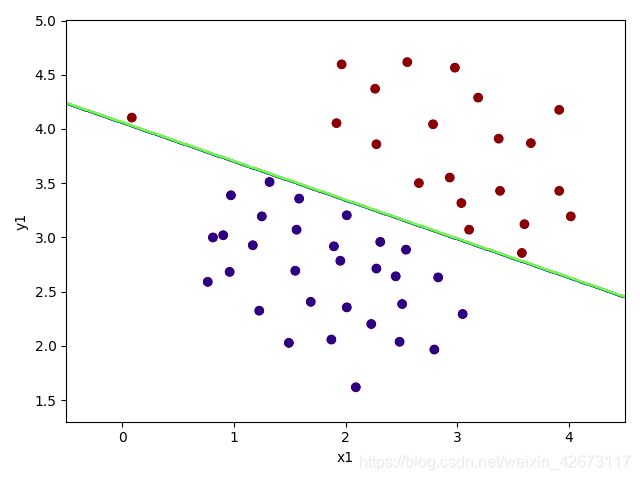
plot_boundary(svc1)
plot_data()

讲解：通过图像分析x和y的较小值和较大值，然后生成x、y的网格，然后将二者拉成一位数组并合并进行预测，预测完成之后再将其拆成二维,然后将其进行绘制

想了一晚上也没想出来他是咋绘制出来的这条等高线，三个二维（500*500）确定出来了一条等高线？？？？

初步想的结果是，两个平面确定了一个三维图形，然后用一个平面对其进行切割，切出来的轮廓是等高线类似的投影到平面上，形成了分界线

结果：

我们发现：最偏的那一个点跑偏了，所以要调整一下C

5、将C调整为100然后进行再次拟合

svc100 = SVC(C=100,kernel='linear')
svc100.fit(X,y.flatten())
print(svc100.score(X,y.flatten()))

结果为100%了
边界显示：

但是这样分类也不是很好，因为边界上的两个点很明显为异常点