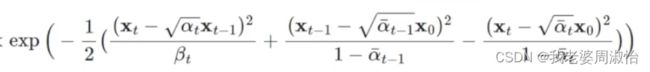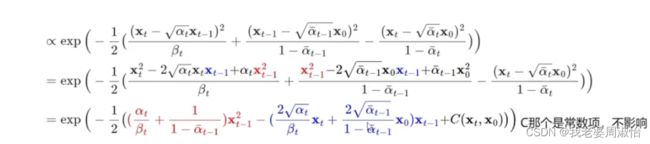Diffusion Model算法
Diffusion Model算法
- 导语
- 1.为什么叫扩散算法
- 2.Diffusion算法理论
-
- 2.1 前向过程
- 2.1.1 公式推导
- 2.2 后向过程(去噪过程)
- 2.2.1 公式推导
- 3.算法流程
导语
最近AI绘画应用如火如荼，
有关算法的应用产品也很多，比如DALLE2
官网地址：https://openai.com/dall-e-2/
DALLE2产品描述：DALL·E2是一个新的人工智能系统，可以根据自然语言的描述创建逼真的图像和艺术
其主要功能有：
- DALLE 2可以从文本描述中创建原创、逼真的图像和艺术。它可以组合概念、属性和样式。
- DALLE 2可以通过自然语言字幕对现有图像进行逼真的编辑。它可以添加和删除元素，同时考虑阴影、反射和纹理。
- DALLE 2可以将图像扩展到原始画布之外，创造出更广阔的新构图
- DALLE 2可以创建不同的灵感来源于原作。
1.为什么叫扩散算法
AI绘画架构，核心算法就是运用了Diffusion（扩散算法）
举个列子：之前三亚出现游客聚集性新冠，如果当时不选择集中隔离，而是允许游客自由进出，那原本集中在一起的游客病例的特征（也可以说是病例轨迹），因为扩散开来，回到各个城市，那不同的游客的病例特征（病例轨迹）也会因此多样化了。
回到图像中，游客的病例特征也就是对应到图像的特征上（最直接的特征就是图像直方图）
对比以前的GAN也是图像生成的算法
GAN缺点：
- GAN训练两个网络，难度较大
- 不容易收敛，而且多样性比较差,只关注能骗过判别器
GAN所能生成出的图像，其图像特征多样性较差，在训练中，只需要生成器生成的图像能满足当前的判别器，使判别器不能识别出假的即可了。
2.Diffusion算法理论
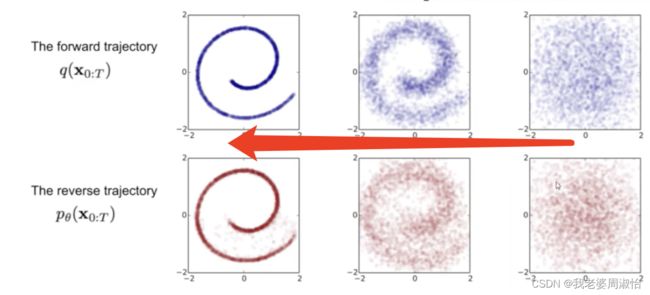
Diffusion算法可以根据结构，有二个方向分成是前向过程和反向过程
2.1 前向过程
核心：不断对输入的图像数据加入噪声，最后变成一个纯噪声的数据
已知最初的原始图像的数据，前向过程，就是需要求得每一个 t t t时刻的图像数据
也就是已知 x 0 x_0 x0,求 x 2 , . . . , x t x_2,...,x_t x2,...,xt
每一个时刻添加一个高斯噪声，
由 x 0 x_0 x0到 x 1 x_1 x1… x N x_N xN时刻
每个时刻 t t t，加入的噪声是不同的，并且加入噪声的数量，会随着时间，越来越多。
2.1.1 公式推导
设 t t t时刻噪声的值 z 1 z_1 z1，是服从高斯分布的，所有噪声都是服从高斯分布的
设 t t t时刻噪声值的权重为 α t \alpha_t αt
α t = 1 − β t \alpha_t=1-\beta_t αt=1−βt，通过 β \beta β来调节 α \alpha α的值， β \beta β是一个小于1的值， β \beta β越来越大， α \alpha α越来越小。
通过 α \alpha α来调节，每个时刻的噪声数量，随着时间，噪声越来越大。
设 t t t时刻的图像分布为 x t x_t xt
x t x_t xt时刻的分布，是由 t − 1 t-1 t−1时刻 x t − 1 x_{t-1} xt−1加入噪声得到的，于是得：
x t = α t x t − 1 + 1 − α t z t x_t=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z_t xt=αtxt−1+1−αtzt
其中 1 − α t = β t \sqrt{1-\alpha_t}=\sqrt{\beta_t} 1−αt=βt
如何得到 x t x_t xt，可以通过 x t − 1 x_{t-1} xt−1得到， x t − 1 x_{t-1} xt−1由 x t − 2 x_{t-2} xt−2,依次递归到 x 0 x_0 x0得到
但 是 太 慢 了 ， 运 算 时 间 过 长 ， 目 前 我 们 已 知 的 就 只 有 x 0 , 如 何 将 x t 用 x 0 去 表 示 但是太慢了，运算时间过长，目前我们已知的就只有x_0,如何将x_t用x_0去表示 但是太慢了，运算时间过长，目前我们已知的就只有x0,如何将xt用x0去表示
步骤1
首先将 x t − 1 = α t − 1 x t − 2 + 1 − α t − 1 z 2 x_{t-1}=\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}z_2 xt−1=αt−1xt−2+1−αt−1z2 带入到 x t = α t x t − 1 + 1 − α t z t x_t=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z_t xt=αtxt−1+1−αtzt中得
x t = α t ( α t − 1 x t − 2 + 1 − α t − 1 z 2 ) + 1 − α t z 1 x_t = \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}z_2)+\sqrt{1-\alpha_t}z_1 xt=αt(αt−1xt−2+1−αt−1z2)+1−αtz1
步骤2：合并高斯分布
已知每次加入的噪声都服从高斯分布 z 1 , z 2 , . . . N ( 0 , I ) z_1,z_2,...~N(0,I) z1,z2,... N(0,I)
x t = α t α t − 1 x t − 2 + ( α t ( 1 − α t − 1 ) z 2 + 1 − α t z 1 ) x_t=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+(\sqrt{\alpha_t(1-\alpha_{t-1})}z_2+\sqrt{1-\alpha_t}z_1) xt=αtαt−1xt−2+(αt(1−αt−1)z2+1−αtz1)
这里有二个高斯分布 N ( 0 , 1 − α t ) N(0,1-\alpha_t) N(0,1−αt), N ( 0 , α t ( 1 − α t − 1 ) ) N(0,\alpha_t(1-\alpha_{t-1})) N(0,αt(1−αt−1))
由数学公式可以推导若两个独立的高斯分布 N 1 ( u 1 , σ 1 2 ) N_1 ~(u_1,\sigma_1^2) N1 (u1,σ12), N 2 ( u 2 , σ 2 2 ) N_2 ~(u_2,\sigma_2^2) N2 (u2,σ22)，其合并后为 N ( u , σ 2 ) N ~(u,\sigma^2) N (u,σ2)
其中 u = u 1 + u 2 u=u_1+u_2 u=u1+u2， σ 2 = σ 1 2 + σ 2 2 \sigma^2=\sigma_1^2+\sigma_2^2 σ2=σ12+σ22
因此 N ( 0 , 1 − α t ) N(0,1-\alpha_t) N(0,1−αt), N ( 0 , α t ( 1 − α t − 1 ) ) N(0,\alpha_t(1-\alpha_{t-1})) N(0,αt(1−αt−1))合并为 N ( 0 , ( 1 − α t ) 2 + α t 2 ( 1 − α t − 1 ) 2 ) N(0,(1-\alpha_t)^2+\alpha_t^2(1-\alpha_{t-1})^2) N(0,(1−αt)2+αt2(1−αt−1)2)
化简后得
x t = α t α t − 1 x t − 2 + 1 − α t α t − 1 z 3 x_t=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}z_3 xt=αtαt−1xt−2+1−αtαt−1z3
其中 z 3 z_3 z3为高斯分布 z 1 , z 2 z_1,z_2 z1,z2的合并
步骤3
既然 x t x_t xt可以直接通过 x t − 2 x_{t-2} xt−2，那一直推导到 x 0 x_0 x0由此可得
x t = α ˉ t x 0 + 1 − α ˉ t z t x_t=\sqrt{\bar \alpha_t}x_0+\sqrt{1-\bar \alpha_t} z_t xt=αˉtx0+1−αˉtzt
其中 α ˉ t = α t ∗ α t − 1 ∗ α t − 2 ∗ α t − 3 ∗ . . . . ∗ α 0 \bar \alpha_t=\alpha_t*\alpha_{t-1}*\alpha_{t-2}*\alpha_{t-3}*....*\alpha_0 αˉt=αt∗αt−1∗αt−2∗αt−3∗....∗α0
现在我们知道了，正向过程，如何由图像转为噪音点图像，现在我们要反过来思考怎么由噪声图像还原到原图像，也叫去噪的过程
也就是已知 x t x_t xt,求 x t − 1 , . . . , x 0 x_{t-1},...,x_0 xt−1,...,x0
2.2 后向过程(去噪过程)
已知 x t x_t xt,求 x t − 1 , . . . , x 0 x_{t-1},...,x_0 xt−1,...,x0
通过贝叶斯公式，可以得：
我们可以通过先验条件 x 0 x_0 x0来求得后验条件 x t − 1 x_{t-1} xt−1或 x t x_t xt，或任何一个 t t t时刻的 x x x值。也就是说 P ( x t − 1 ∣ x 0 ) P(x_{t-1}|x_0) P(xt−1∣x0), P ( x t ∣ x 0 ) P(x_t|x_0) P(xt∣x0)已知
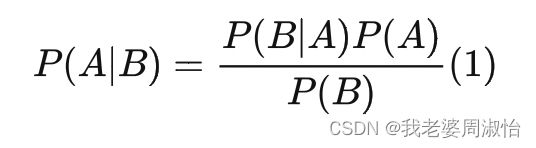
目的是反向推理： P ( x t − 1 ∣ x t ) P(x_{t-1}|x_t) P(xt−1∣xt)，先验条件为 x t x_t xt，求后验条件 x t − 1 x_{t-1} xt−1，公式如下：
P ( x t − 1 ∣ x t ) = P ( x t ∣ x t − 1 ) P ( x t − 1 ) P ( x t ) P(x_{t-1}|x_t)=\frac{P(x_t|x_{t-1})P(x_{t-1})}{P(x_t)} P(xt−1∣xt)=P(xt)P(xt∣xt−1)P(xt−1)
其中 P ( x t − 1 ) P(x_{t-1}) P(xt−1), P ( x t ) P(x_t) P(xt)可以通过先验条件 x 0 x_0 x0求得
也就是 P ( x t − 1 ∣ x 0 ) P(x_{t-1}|x_0) P(xt−1∣x0), P ( x t ∣ x 0 ) P(x_t|x_0) P(xt∣x0)
2.2.1 公式推导
步骤1
因为 P ( x t − 1 ) , P ( x t ) P(x_{t-1}),P(x_t) P(xt−1),P(xt)都可以通过先验条件 x 0 x_0 x0求得，虽然这里 x 0 x_0 x0未知，但可以将 P ( x t − 1 ∣ x t ) = P ( x t ∣ x t − 1 ) P ( x t − 1 ) P ( x t ) P(x_{t-1}|x_t)=\frac{P(x_t|x_{t-1})P(x_{t-1})}{P(x_t)} P(xt−1∣xt)=P(xt)P(xt∣xt−1)P(xt−1)表示为：
P ( x t − 1 ∣ x t , x 0 ) = P ( x t ∣ x t − 1 , x 0 ) P ( x t − 1 ∣ x 0 ) P ( x t ∣ x 0 ) P(x_{t-1}|x_t,x_0)=P(x_t|x_{t-1},x_0)\frac{P(x_{t-1}|x_0)}{P(x_t|x_0)} P(xt−1∣xt,x0)=P(xt∣xt−1,x0)P(xt∣x0)P(xt−1∣x0)
其中 P ( x t − 1 ∣ x 0 ) = α ˉ t − 1 x 0 + 1 − α ˉ t − 1 z P(x_{t-1}|x_0)=\sqrt{\bar\alpha_{t-1}}x_0+\sqrt{1-\bar \alpha_{t-1}}z P(xt−1∣x0)=αˉt−1x0+1−αˉt−1z ~ N ( α ˉ t − 1 x 0 , 1 − α ˉ t − 1 ) N(\sqrt{\bar\alpha_{t-1}}x_0,1-\bar\alpha_{t-1}) N(αˉt−1x0,1−αˉt−1)
其中 P ( x t ∣ x 0 ) = α ˉ t x 0 + 1 − α ˉ t z P(x_t|x_0)=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar \alpha_t}z P(xt∣x0)=αˉtx0+1−αˉtz ~ N ( α ˉ t x 0 , 1 − α ˉ t ) N(\sqrt{\bar\alpha_t}x_0,1-\bar\alpha_t) N(αˉtx0,1−αˉt)
其中 P ( x t ∣ x t − 1 , x 0 ) = α t x t − 1 + 1 − α t z P(x_t|x_{t-1},x_0)=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z P(xt∣xt−1,x0)=αtxt−1+1−αtz ~ N ( α t x t − 1 , 1 − α t ) N(\sqrt{\alpha_t}x_{t-1},1-\alpha_t) N(αtxt−1,1−αt)
步骤2
从式子中可以看到都包含一个 z z z的高斯分布（正态分布）
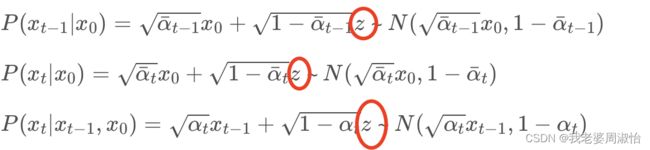
由高斯分布公式：
可以将三个式子通过正态分布换算为：
把正态分布展开后，乘法相当于加法，除法相当于减法。
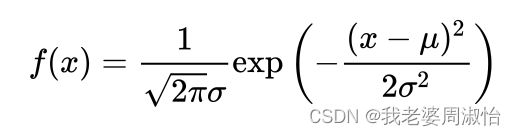
步骤3
化简步骤2得：
u ^ t ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + α ˉ t − 1 β t 1 − α ˉ t x 0 \hat u_t(x_t,x_0)=\frac{\sqrt{\alpha_t}(1-\bar \alpha_{t-1})}{1-\bar \alpha_t}x_t+\frac{\sqrt{\bar \alpha_{t-1}}\beta_t}{1-\bar \alpha_t}x_0 u^t(xt,x0)=1−αˉtαt(1−αˉt−1)xt+1−αˉtαˉt−1βtx0
其中 x 0 = 1 α ˉ t ( x t − 1 − α ˉ t z t ) x_0=\frac{1}{\sqrt{\bar \alpha_t}}(x_t-\sqrt{1-\bar \alpha_t}z_t) x0=αˉt1(xt−1−αˉtzt)
最终结果求出：
u ^ t = 1 α t ( x t − β t 1 − α ˉ t z ˉ t ) \hat u_t=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar \alpha_t}}\bar z_t) u^t=αt1(xt−1−αˉtβtzˉt)
如果上面的公式计算看不懂，只需要记住这最后这个式子即可。
3.算法流程
模型的训练和预测，并通过损失函数来拟合，一直是围绕着噪声 Z t Z_t Zt来求解的
前向过程：我们随机增加的噪声——>噪声就是已知的标签 y y y
反向过程：通过模型预测出前面时刻的图像，来还原，已知 x t x_t xt，求得 x t − 1 x_{t-1} xt−1，也就得到了中间的噪声 y ^ \hat y y^。
用前向反向的噪声来作为损失函数，来拟合模型
模型整体主干结构选择U-Net
算法流程图
Algorithm 1 Training
算法训练
- 从 q ( x 0 ) q(x_0) q(x0)图像中采样得到一部分图像 x 0 x_0 x0
- 设置t，每张图片的t时刻是不固定的，比如batch =4 第一张。t=30，第二张 t=150
- 加噪声 ϵ \epsilon ϵ
- 噪声和模型预测的噪声 ，损失函数
Algorithm 2 Samping
模型训练完，就不需要前向过程，只用反向做预测
- 输入不同 t t t时刻的图像
- 随机采样一个 t t t，求 x t − 1 x_{t-1} xt−1
- 这里流程4中的公式，就是 u ^ t = 1 α t ( x t − β t 1 − α ˉ t z ˉ t ) \hat u_t=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar \alpha_t}}\bar z_t) u^t=αt1(xt−1−αˉtβtzˉt)