2022美赛C题 预测模型
由于影响资产价格的波动机理非常复杂,难以简单的运用数学模型加以解释,数据量较大需预处理且非平稳波动,很难利用传统的统计学模型和计量经济学模型预测。而神经网络这种高度复杂的非线性自学习抽象人工模拟,具有分布式存储,自组织,自适应能力。其上述特点使得它更适合处理如股票预测这样不稳定,类随机的复杂非线性的时间序列训练预测问题。LSTM这种神经网络,具备时序观念,可以实现对时间序列远期走势进行预测分析
LSTM:(Long Short-Term Memory)长短时记忆模型,是建立在RNN上的一种深度学习神经网络,在输入,反馈与防止梯度爆炸之间建立了一个长时间的时滞,使得梯度既不会爆发也不会消失。通过引入门机制,通过输入门,输出门和忘记门来选择性记忆反馈的误差函数随梯度下降的修正参数,解决了RNN模型不具备的长记忆性问题用。它的选择性记忆性以及时序内部影响的特性即为极适用于股票价格预测这种类随机的非平稳序列。
代码:
以黄金预估为例,比特币更好处理,因为比特币没有空值,文件位置改一下就可以。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import math
from keras.models import Sequential
from keras.layers import Dense, Activation, Dropout, LSTM
from sklearn.preprocessing import MinMaxScaler # 归一化的包,归一化后数据小,运行快
from sklearn.metrics import mean_squared_error # 评价模型好坏的指标,相对来说越小越好
import time
"""
预测值在时间维度上的走势
"""
"""
创建变量x和y,LSTM的x和y全是一组数据产生的,自己和之前的自己比。
look_back:回溯,即用前n个数据预测第n+1个数据
"""
def creat_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset) - look_back - 1):
a = dataset[i: (i + look_back)]
dataX.append(a)
dataY.append(dataset[i + look_back])
return np.array(dataX), np.array(dataY)
if __name__ == '__main__':
"""
空值填补为前一个值
"""
dataframe = pd.read_csv('LBMA-GOLD.csv',
header=0, # 取消第一行作为表头
parse_dates=[0], # 指定某行读取为日期格式
index_col=0, # 用作行索引的列编号或者列名,如果给定一个序列则有多个行索引。
usecols=[0, 1], # 返回一个数据子集,只读取0,1两列
squeeze=True) # True的情况下返回的类型为Series,目的:下一步画图
# print(np.isnan(dataframe).any()) # 检测是否有空值
dataframe.dropna(inplace=True) # 删除缺失值
dataset = dataframe.values # 对应的二维NumPy值数组 # 报错:相同的代码块,存在于不同的文件
print(dataframe.head(10))
"""
利用Pandas库对Series数据结构的数据的图形化展示
"""
plt.figure(figsize=(12, 8))
dataframe.plot() # 针对向量或矩阵的列来绘制二维图形
plt.plot(color="orange")
plt.ylabel('price')
plt.yticks(np.arange(1000, 2250, 250)) # 改变纵坐标刻度; 返回一个有终点和起点的固定步长的排列
plt.show()
"""
归一化
"""
scaler = MinMaxScaler(feature_range=(0, 1)) # 所有数据标准化到0-1区间内
dataset = scaler.fit_transform(dataset.reshape(-1, 1)) # 先拟合fit,再转换transform,从而实现数据的标准化、归一化
"""
测试集和训练集分割,8:2
问题:可优化或调试,
"""
train_size = int(len(dataset) * 0.8)
test_size = len(dataset) - train_size
train, test = dataset[0: train_size], dataset[train_size: len(dataset)]
"""
调用前面函数分别生成训练集和测试集的x,y
"""
look_back = 1
trainX, trainY = creat_dataset(train, look_back)
testX, testY = creat_dataset(test, look_back)
"""
建模:多层lstm
"""
model = Sequential() # 开始构建model,实例化模型
# .add()将各层添加到网络中,input_dim输入维度,首层指定,return_sequences,控制返回类型,返回整个序列
model.add(LSTM(input_dim=1, units=50, return_sequences=True))
model.add(LSTM(input_dim=50, units=100, return_sequences=True))# unit神经元,输出维度
model.add(LSTM(input_dim=100, units=200, return_sequences=True))
model.add(LSTM(300, return_sequences=False))
model.add(Dropout(0.2))
model.add(Dense(100)) # Dense是一个全连接层
model.add(Dense(units=1))
model.add(Activation('relu')) # 传递激活函数relu
start = time.time()
model.compile(loss='mean_squared_error', optimizer='Adam')
model.summary()
"""
训练的历史过程
"""
history = model.fit(trainX, trainY, batch_size=64, epochs=50,
validation_split=0.1, verbose=2)
print('compilatiom time:', time.time() - start)
"""
代入数据
"""
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
"""
归一化的测试评分
"""
trainScore = math.sqrt(mean_squared_error(trainY, trainPredict[:, 0]))
print('Train Score1 %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY, testPredict[:, 0]))
print('Test Score1 %.2f RMSE' % (testScore))
"""
反归一化,恢复原来数据范围
"""
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform(trainY)
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform(testY)
"""
反归一化的评分
"""
trainScore = math.sqrt(mean_squared_error(trainY, trainPredict[:, 0]))
print('Train Score2 %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY, testPredict[:, 0]))
print('Test Score2 %.2f RMSE' % (testScore))
trainPredictPlot = np.empty_like(dataset) # 返回形状和大小与给定数组相似的数组
trainPredictPlot[:] = np.nan # 全为空
trainPredictPlot = np.reshape(trainPredictPlot, (dataset.shape[0], 1))
trainPredictPlot[look_back: len(trainPredict) + look_back, :] = trainPredict
testPredictPlot = np.empty_like(dataset)
testPredictPlot[:] = np.nan
testPredictPlot = np.reshape(testPredictPlot, (dataset.shape[0], 1))
testPredictPlot[len(trainPredict) + (look_back * 2) + 1: len(dataset) - 1, :] = testPredict
"""
画图:记录训练过程(前面history)中的参数变化,如loss
"""
fig1 = plt.figure(figsize=(12, 8))
plt.style.use('seaborn')
plt.plot(history.history['loss'], color='#FF8C00')
plt.title('LSTM Gold Model Loss', fontsize=34)
plt.ylabel('Loss', fontsize=30)
plt.xlabel('Epoch', fontsize=30)
plt.tick_params(labelsize=26)
plt.show()
"""
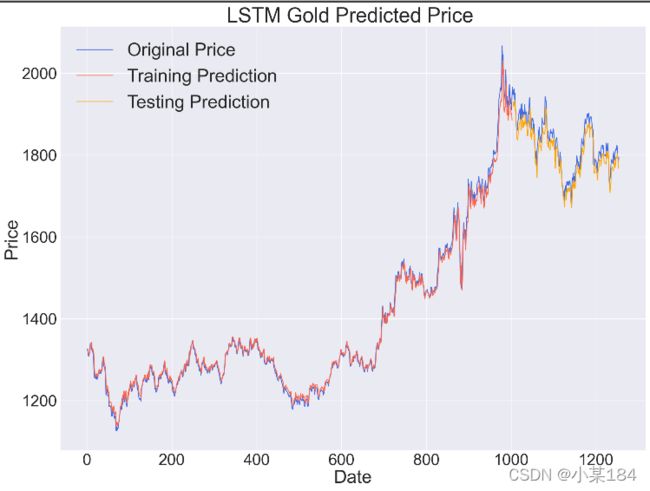
画图:蓝色————原始数据;红色————训练数据训练完再进行预测的。黄色————测试数据
"""
fig2 = plt.figure(figsize=(20, 15))
plt.plot(scaler.inverse_transform(dataset), color='royalblue', label='Original Price')
plt.plot(trainPredictPlot, color="tomato", label='Training Prediction ')
plt.plot(testPredictPlot, color="orange", label='Testing Prediction')
plt.title('LSTM Gold Predicted Price ', fontsize=45, )
plt.ylabel('Price', fontsize=40)
plt.xlabel('Date', fontsize=40)
plt.tick_params(labelsize=35)
plt.legend(fontsize=40)
plt.show()
"""
放大预测部分,
"""
fig3 = plt.figure(figsize=(20, 15))
plt.plot(np.arange(train_size + 1, len(dataset) + 1, 1), scaler.inverse_transform(dataset)[train_size:],
label='Dataset', color="royalblue")
plt.plot(testPredictPlot, color='orange', label='Test', markersize=12)
plt.title('LSTM Gold Predict Price Enlarge Image ', fontsize=45)
plt.ylabel('Price', fontsize=40)
plt.xlabel('Date', fontsize=40)
plt.tick_params(labelsize=35)
plt.legend(fontsize=40)
plt.show()
最后的输出:
Date
2016-09-12 1324.60
2016-09-13 1323.65
2016-09-14 1321.75
2016-09-15 1310.80
2016-09-16 1308.35
2016-09-19 1314.85
2016-09-20 1313.80
2016-09-21 1326.10
2016-09-22 1339.10
2016-09-23 1338.65
Name: USD (PM), dtype: float64
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm (LSTM) (None, None, 50) 10400
_________________________________________________________________
lstm_1 (LSTM) (None, None, 100) 60400
_________________________________________________________________
lstm_2 (LSTM) (None, None, 200) 240800
_________________________________________________________________
lstm_3 (LSTM) (None, 300) 601200
_________________________________________________________________
dropout (Dropout) (None, 300) 0
_________________________________________________________________
dense (Dense) (None, 100) 30100
_________________________________________________________________
dense_1 (Dense) (None, 1) 101
_________________________________________________________________
activation (Activation) (None, 1) 0
=================================================================
Total params: 943,001
Trainable params: 943,001
Non-trainable params: 0
_________________________________________________________________
Epoch 1/50
15/15 - 9s - loss: 0.0290 - val_loss: 0.2381
Epoch 2/50
15/15 - 0s - loss: 0.0162 - val_loss: 0.2958
Epoch 3/50
15/15 - 0s - loss: 0.0154 - val_loss: 0.2487
Epoch 4/50
15/15 - 0s - loss: 0.0114 - val_loss: 0.0483
Epoch 5/50
15/15 - 0s - loss: 0.0017 - val_loss: 0.0021
Epoch 6/50
15/15 - 0s - loss: 6.6580e-04 - val_loss: 0.0030
Epoch 7/50
15/15 - 0s - loss: 3.0745e-04 - val_loss: 5.4789e-04
Epoch 8/50
15/15 - 0s - loss: 2.4054e-04 - val_loss: 7.9501e-04
Epoch 9/50
15/15 - 0s - loss: 2.0958e-04 - val_loss: 0.0012
Epoch 10/50
15/15 - 0s - loss: 1.8985e-04 - val_loss: 5.4934e-04
Epoch 11/50
15/15 - 0s - loss: 1.8904e-04 - val_loss: 5.5279e-04
Epoch 12/50
15/15 - 0s - loss: 1.8975e-04 - val_loss: 0.0011
Epoch 13/50
15/15 - 0s - loss: 2.5828e-04 - val_loss: 0.0018
Epoch 14/50
15/15 - 0s - loss: 2.0057e-04 - val_loss: 7.1245e-04
Epoch 15/50
15/15 - 0s - loss: 1.7724e-04 - val_loss: 5.5000e-04
Epoch 16/50
15/15 - 0s - loss: 1.9647e-04 - val_loss: 0.0014
Epoch 17/50
15/15 - 0s - loss: 2.4390e-04 - val_loss: 0.0012
Epoch 18/50
15/15 - 0s - loss: 1.7508e-04 - val_loss: 8.3849e-04
Epoch 19/50
15/15 - 0s - loss: 1.8564e-04 - val_loss: 6.9165e-04
Epoch 20/50
15/15 - 0s - loss: 2.0548e-04 - val_loss: 7.1624e-04
Epoch 21/50
15/15 - 0s - loss: 2.4446e-04 - val_loss: 5.6699e-04
Epoch 22/50
15/15 - 0s - loss: 1.9528e-04 - val_loss: 5.4511e-04
Epoch 23/50
15/15 - 0s - loss: 1.9244e-04 - val_loss: 0.0016
Epoch 24/50
15/15 - 0s - loss: 2.2294e-04 - val_loss: 9.3757e-04
Epoch 25/50
15/15 - 0s - loss: 2.4636e-04 - val_loss: 5.4590e-04
Epoch 26/50
15/15 - 0s - loss: 1.9207e-04 - val_loss: 5.5049e-04
Epoch 27/50
15/15 - 0s - loss: 1.9909e-04 - val_loss: 7.3373e-04
Epoch 28/50
15/15 - 0s - loss: 2.0031e-04 - val_loss: 5.4550e-04
Epoch 29/50
15/15 - 0s - loss: 1.8701e-04 - val_loss: 5.2237e-04
Epoch 30/50
15/15 - 0s - loss: 1.8367e-04 - val_loss: 5.4638e-04
Epoch 31/50
15/15 - 0s - loss: 1.9273e-04 - val_loss: 6.6556e-04
Epoch 32/50
15/15 - 0s - loss: 1.9833e-04 - val_loss: 7.1173e-04
Epoch 33/50
15/15 - 0s - loss: 2.0197e-04 - val_loss: 5.2020e-04
Epoch 34/50
15/15 - 0s - loss: 1.7008e-04 - val_loss: 5.8340e-04
Epoch 35/50
15/15 - 0s - loss: 1.9542e-04 - val_loss: 8.7973e-04
Epoch 36/50
15/15 - 0s - loss: 1.8401e-04 - val_loss: 6.0528e-04
Epoch 37/50
15/15 - 0s - loss: 1.8716e-04 - val_loss: 0.0012
Epoch 38/50
15/15 - 0s - loss: 2.0904e-04 - val_loss: 6.3759e-04
Epoch 39/50
15/15 - 0s - loss: 2.0505e-04 - val_loss: 8.5336e-04
Epoch 40/50
15/15 - 0s - loss: 1.9915e-04 - val_loss: 5.6953e-04
Epoch 41/50
15/15 - 0s - loss: 1.8749e-04 - val_loss: 5.2926e-04
Epoch 42/50
15/15 - 0s - loss: 1.9252e-04 - val_loss: 7.3856e-04
Epoch 43/50
15/15 - 0s - loss: 2.1674e-04 - val_loss: 7.5678e-04
Epoch 44/50
15/15 - 0s - loss: 2.0391e-04 - val_loss: 8.6106e-04
Epoch 45/50
15/15 - 0s - loss: 2.2076e-04 - val_loss: 5.3117e-04
Epoch 46/50
15/15 - 0s - loss: 1.7045e-04 - val_loss: 6.8105e-04
Epoch 47/50
15/15 - 0s - loss: 1.7648e-04 - val_loss: 7.0672e-04
Epoch 48/50
15/15 - 0s - loss: 1.6500e-04 - val_loss: 5.3536e-04
Epoch 49/50
15/15 - 0s - loss: 2.0319e-04 - val_loss: 6.8779e-04
Epoch 50/50
15/15 - 0s - loss: 2.1893e-04 - val_loss: 0.0011
compilatiom time: 16.615519285202026
Train Score 0.02 RMSE
Test Score 0.03 RMSE
Train Score 15.59 RMSE
Test Score 26.91 RMSE
Process finished with exit code 0
最后的图像:
随着训练次数增加,其误差迅速逐渐降低后基本不变
蓝色是原始数据,红色是验证集结果。橙色是测试集预估价格。根据图像可以看到LSTM很好的预估了黄金的价格走势,图像基本符合。
通过放大测试集部分图像可以看到,在峰值部分存在些许偏差。